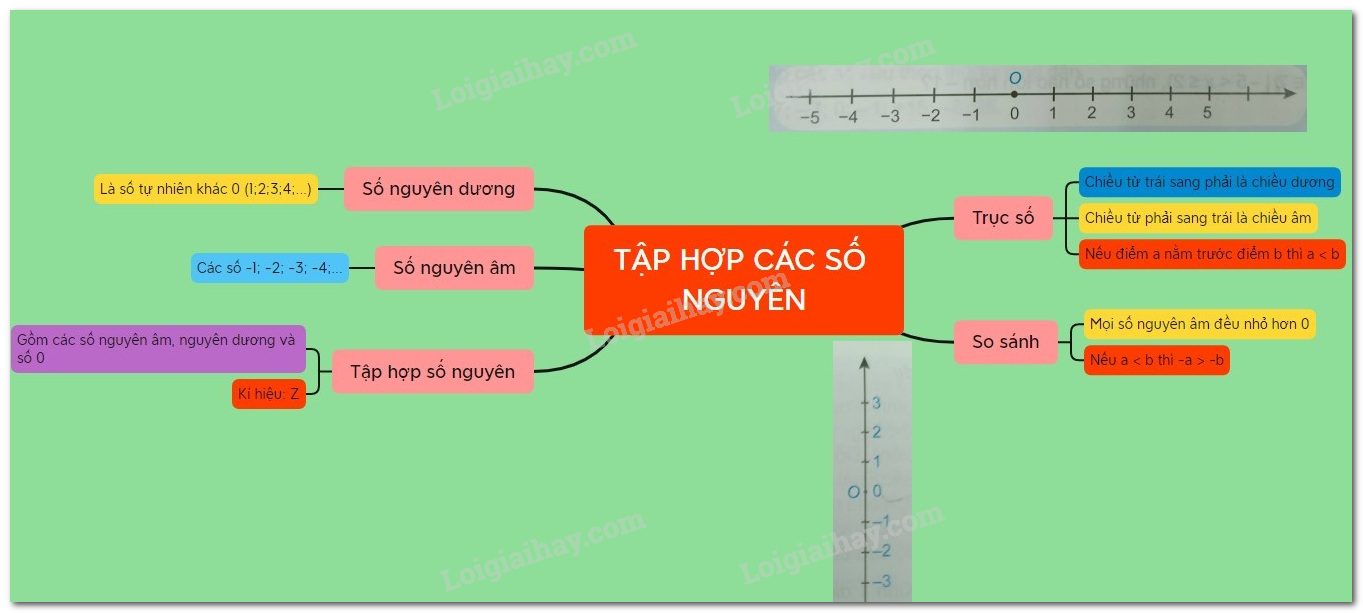
Lý thuyết Tập hợp các số nguyên Toán 6 Cánh diều
Lý thuyết Tập hợp các số nguyên Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
I. Tập hợp Z các số nguyên
- Số tự nhiên khác 0 còn được gọi là số nguyên dương
- Các số nguyên âm, số 0 và các số nguyên dương tạo thành tập hợp các số nguyên
- Tập hợp các số nguyên được kí hiệu là Z
II. Biểu diễn số nguyên trên trục số
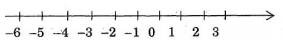
+ Trên trục số nằm ngang : Điểm \(0\)được gọi là điểm gốc của trục số. Chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm của trục số.
+ Trên trục số thẳng đứng , điểm biểu diễn số nguyên âm nằm dưới điểm 0, điểm biểu diễn số nguyên dương nằm trên điểm 0
+ Điểm biểu diễn số nguyên \(a\) trên trục số gọi là điểm \(a.\)
+) Cho số nguyên \(a\) và \(b\). Trên trục số, nếu điểm \(a\) nằm bên trái điểm \(b\) thì số \(a\) nhỏ hơn số \(b\), kí hiệu \(a < b\)
Ví dụ :
Số 2 trên trục số được gọi là điểm 2.
Số \( - 9\) trên trục số được gọi là điểm \( - 9\)
Ví dụ: Cho trục số như hình vẽ.

Ta thấy điểm biểu diễn số \( - 5\) nằm bên trái điểm biểu diễn số \( - 3\) nên \( - 5 < - 3.\)
III. Số đối của một số nguyên
- Trên trục số, hai số nguyên (phân biệt) có điểm biểu diễn nằm về 2 phía của gốc 0 và cách đều gốc 0 được gọi là 2 số đối nhau
- Số đối của số 0 là 0
IV. So sánh các số nguyên
Cho số nguyên \(a\) và \(b\).
Trên trục số nằm ngang, nếu điểm \(a\) nằm bên trái điểm \(b\) thì số \(a\) nhỏ hơn số \(b\), kí hiệu \(a < b\)
Trên trục số thẳng đứng, nếu điểm \(a\) nằm bên dưới điểm \(b\) thì số \(a\) nhỏ hơn số \(b\), kí hiệu \(a < b\)
Ví dụ: Cho trục số như hình vẽ.
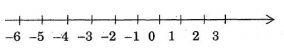
Ta thấy điểm biểu diễn số \( - 5\) nằm bên trái điểm biểu diễn số \( - 3\) nên \( - 5 < - 3.\)
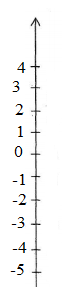
Ta thấy điểm biểu diễn số -2 nằm bên dưới điểm biểu diễn số 1 nên \(-2<1\)
- Mọi số nguyên âm đều nhỏ hơn số nguyên dương.
- Để so sánh 2 số nguyên âm, ta làm 2 bước sau:
Bước 1: Bỏ dấu "-" trước cả 2 số âm
Bước 2: Trong 2 số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu( trước khi bỏ dấu "-" lớn hơn
Chú ý:
- Mọi số nguyên âm đều nhỏ hơn 0.
- Mọi số nguyên dương đều lớn hơn 0.
- Nếu \(a,b\) là hai số nguyên dương và \(a > b\) thì \( - a < - b\) (Thêm dấu “-” thì đổi dấu “>” thành dấu “<”)
- Nếu \(a,b\) là hai số nguyên dương và \(a < b\) thì \( - a > - b\)
- Kí hiệu \(a \le b\) có nghĩa là “\(a < b\) hoặc \(a = b\)”
- Kí hiệu \(a \ge b\) có nghĩa là “\(a > b\) hoặc \(a = b\)”
Ví dụ :
5 là số nguyên dương và \( - 25\) là số nguyên âm nên \(5 > - 25\)
Vì \(15 > 3\) nên \( - 15 < - 3\)