Lý thuyết tính chất kết hợp của phép nhân
a) Tính rồi so sánh giá trị của hai biểu thức:
a) Tính rồi so sánh giá trị của hai biểu thức:
$(2 \times 3) \times 4$ và $2 \times (3 \times 4)$
Ta có: $(2 \times 3) \times 4 = 6 \times 4 = 24$
$2 \times (3 \times 4) = 2 \times 12 = 24$
Vậy: $(2 \times 3) \times 4 = 2 \times (3 \times 4)$
b) So sánh giá trị của hai biểu thức $(a \times b) \times c$ và $a \times (b \times c)$ trong bảng sau:
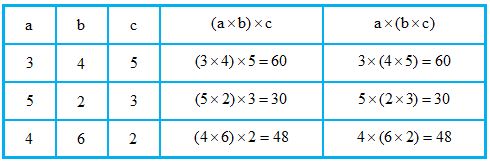
Ta thấy giá trị của $(a \times b) \times c$ và của $a \times (b \times c)$ luôn bằng nhau, ta viết:
\((a\, \times b) \times c = a \times (b\, \times c)\)
Khi nhân một tích hai số với số thứ ba, ta có thể nhân số thứ nhất với tích của số thứ hai và số thứ ba.
Chú ý: Ta có thể tính giá trị của biểu thức dạng $a \times b \times c$ như sau:
\(a\, \times b\, \times c = (a\, \times b) \times c = a \times (b\, \times c)\)