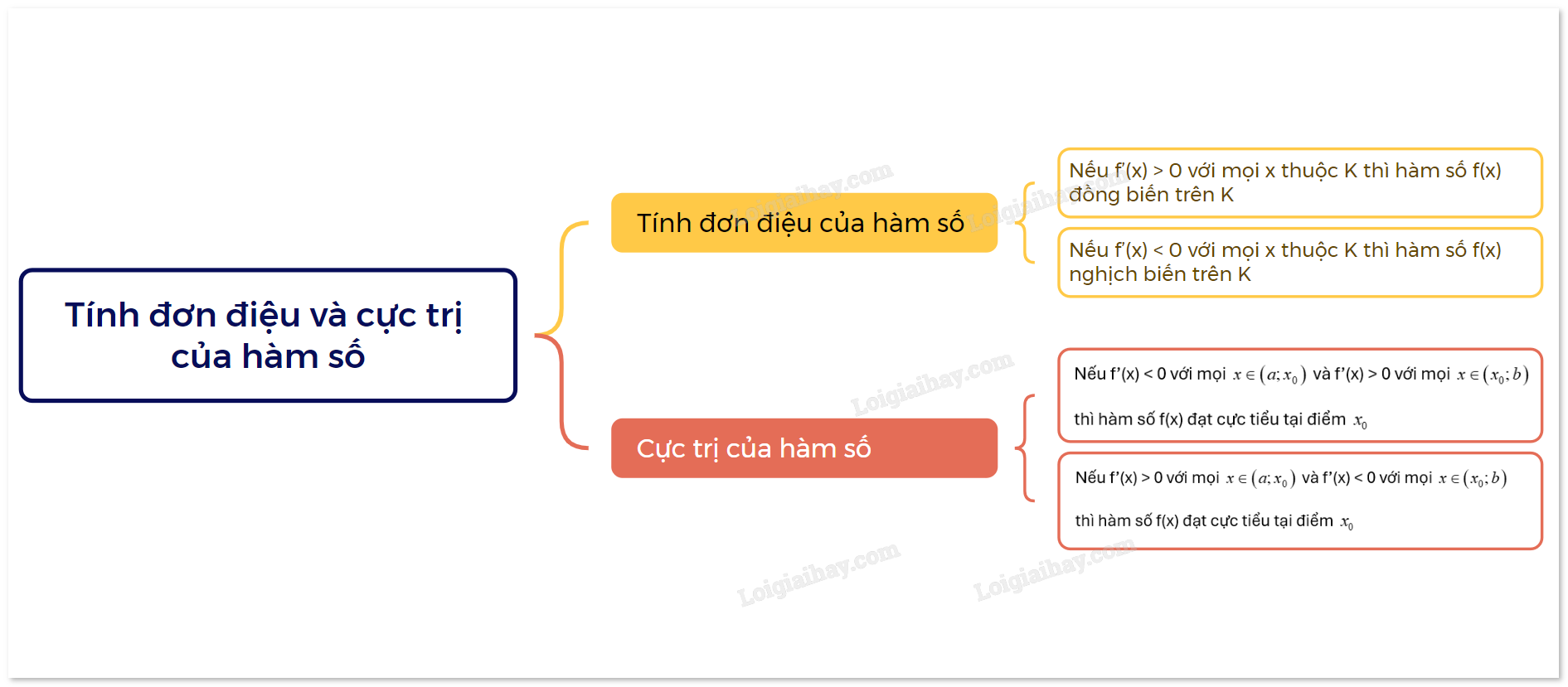
Lý thuyết Tính đơn điệu và cực trị của hàm số Toán 12 Chân trời sáng tạo — Không quảng cáo

Cho hàm số y = f(x) có đạo hàm trên K

• Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
• Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

Cho hàm số y = f(x) liên tục trên tập \(K \subset R\), trong đó K là một khoảng, đoạn hoặc nửa khoảng và \({x_0} \in K,{x_1} \in K\)

• \({x_0}\) được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm \({x_0}\) sao cho (a;b) \( \subset \) K và \(f(x) < f({x_0})\) với mọi \(x \in (a;b)\) và \(x \ne {x_0}\). Khi đó, \(f({x_0})\) được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là \({f_{CĐ}}\)
• \({x_1}\) được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm \({x_0}\) sao cho (c;d) \( \subset \) K và \(f(x) > f({x_1})\) với mọi \(x \in (c;d)\) và \(x \ne {x_1}\). Khi đó, \(f({x_1})\) được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là \({f_{CT}}\)
• Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị)

Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\) . Khi đó:

a) Nếu f’(x) < 0 với mọi \(x \in \left( {a;{x_0}} \right)\) và f’(x) > 0 với mọi \(x \in \left( {{x_0};b} \right)\) thì hàm số f(x) đạt cực tiểu tại điểm \({x_0}\)