Lý thuyết về diện tích hình thang — Không quảng cáo

Quy tắc: Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho \(2\).

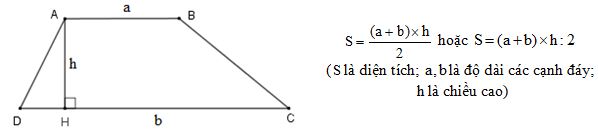
Ví dụ 1: Tính diện tích hình thang biết độ dài hai đáy lần lượt là \(18cm\) và \(14cm\); chiều cao là \(9cm\).

Cách giải:

Diện tích hình thang đó là:

\(\dfrac{{(18 + 14) \times 9}}{2} = 144\left( {c{m^2}} \right)\)

Đáp số: \(144c{m^2}\).

Ví dụ 2: Tính diện tích hình thang biết độ dài hai đáy lần lượt là \(4m\) và \(25dm\); chiều cao là \(32dm\).

Cách giải:

Đổi \(4m = 40dm\)

Diện tích hình thang đó là:

\(\dfrac{{(40 + 25) \times 32}}{2} = 1040\left( {d{m^2}} \right)\)

Đáp số: \(1040d{m^2}\)