Trả lời câu hỏi 1 Bài 2 trang 71 SGK Toán 9 Tập 1
Xét tam giác ABC vuông tại A
Đề bài
Xét tam giác ABC vuông tại A có \(\widehat B = \alpha \) . Chứng minh rằng:
a) \(\displaystyle \alpha = {45^o} \Leftrightarrow {{AC} \over {AB}} = 1\)
b) \(\displaystyle \alpha = {60^o} \Leftrightarrow {{AC} \over {AB}} = \sqrt 3 \)
Phương pháp giải - Xem chi tiết
a) Sử dụng tính chất tam giác cân
b) Sử dụng tính chất tam giác cân và sử dụng định lý Pytago
Lời giải chi tiết
a)
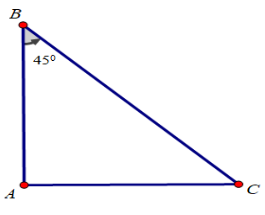
Tam giác ABC vuông tại A có \(\widehat B = {45^o} \Rightarrow \Delta ABC\) vuông cân tại A \( \displaystyle \Rightarrow AB = AC \Rightarrow {{AB} \over {AC}} = 1\)
b)
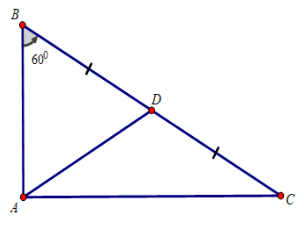
Kẻ trung tuyến AD của tam giác vuông ABC
\( \displaystyle \Rightarrow AD = BD = {{BC} \over 2}\)
Tam giác ABD có: \(AD = BD,\,\,\widehat {ABD} = {60^o}\)
\( \Rightarrow \Delta ABD\) là tam giác đều ( Dấu hiệu nhận biết tam giác đều)
\( \displaystyle \Rightarrow AB = AD = {{BC} \over 2} \Rightarrow BC =2 AB\)
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
\(\eqalign{& A{B^2} + A{C^2} = B{C^2} \cr & \Leftrightarrow A{B^2} + A{C^2} = 4A{B^2} \cr & \Leftrightarrow A{C^2} = 3A{B^2} \Rightarrow AC = \sqrt 3 AB \cr & \Leftrightarrow {{AC} \over {AB}} = \sqrt 3 \cr} \)