Trả lời câu hỏi 1 Bài 2 trang 71 Toán 9 Tập 2
Hãy chứng minh định lý trên.
Đề bài
Hãy chứng minh định lý trên.
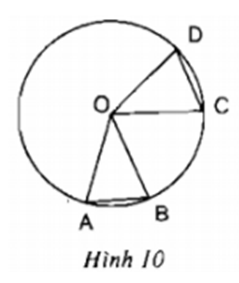
Phương pháp giải - Xem chi tiết
Số đo cung = số đo góc ở tâm chắn cung đó.
Chứng minh hai tam giác bằng nhau để suy ra các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.
Lời giải chi tiết
a) Chứng minh: \(\overparen{AB} = \overparen{CD}\) \( \Rightarrow \) AB = CD
Vì \(\overparen{AB} = \overparen{CD}\) \( \Rightarrow \widehat {AOB} = \widehat {COD}\) (Số đo cung = số đo góc ở tâm chắn cung đó)
Xét \(\Delta OAB\) và \(\Delta OCD\) có:
\(\eqalign{& OA = OC = R \cr & \widehat {AOB} = \widehat {COD} \cr & OB = OD = R \cr & \Rightarrow \Delta OAB = \Delta OCD\,\,\left( {c.g.c} \right) \cr}\)
\( \Rightarrow AB = CD \) ( 2 cạnh tương ứng)
b) Chứng minh: AB = CD \( \Rightarrow \) \(\overparen{AB} = \overparen{CD}\)
Xét \(\Delta OAB\) và \(\Delta OCD\) có:
\(\eqalign{& OA = OC = R \cr & AB = CD\,\,\left( {gt} \right) \cr & OB = OD = R \cr & \Rightarrow \Delta OAB = \Delta OCD\,\,\left( {c.c.c} \right) \cr}\)
\(\Rightarrow \widehat {AOB} = \widehat {COD} \) (2 góc tương ứng)
\( \Rightarrow \) \(\overparen{AB} = \overparen{CD}\) (Số đo góc ở tâm chắn cung = số đo cung đó)