Trả lời câu hỏi 1 Bài 3 trang 105 SGK Toán 9 Tập 1
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
Đề bài
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
a) Nếu AB = CD thì OH = OK.
b) Nếu OH = OK thì AB = CD.
Lời giải chi tiết
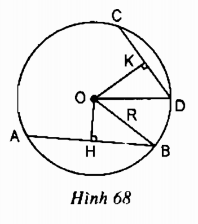
Xét đường tròn \((O)\) có
OH là một phần đường kính vuông góc với dây AB
\( \Rightarrow \) H là trung điểm của \(AB\) (Định lí) \( \Rightarrow AB{\rm{ }} = {\rm{ }}2HB\)
OK là một phần đường kính vuông góc với dây CD
\( \Rightarrow \) K là trung điểm của \(CD\) (Định lí) \( \Rightarrow CD{\rm{ }} = {\rm{ }}2KD\)
Theo mục 1: \(O{H^2} + H{B^2} = O{K^2} + K{D^2}\)
a) Nếu \(AB{\rm{ }} = {\rm{ }}CD \Rightarrow HB{\rm{ }} = {\rm{ }}KD\)
mà \(O{H^2} + H{B^2} = O{K^2} + K{D^2}\) \( \Rightarrow O{H^2} = O{K^2} \Rightarrow OH = OK\)
b) Nếu \(OH = OK \Rightarrow O{H^2} = O{K^2}\)
mà \(O{H^2} + H{B^2} = O{K^2} + K{D^2}\) \( \Rightarrow HB{\rm{ }} = {\rm{ }}KD \Rightarrow AB{\rm{ }} = {\rm{ }}CD\)