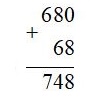Bài 1, 2, 3, 4, 5 trang 177 SGK Toán 4
Bài 1: a) Đọc các số.
Bài 1
a) Đọc các số:
\(975 \;368\) ; \(6\; 020\; 975\) ; \(94\; 351\; 708\) ; \(80\; 060\; 090\)
b) Trong mỗi số trên, chữ số \(9\) ở hàng nào và có giá trị là bao nhiêu ?
Phương pháp giải:
- Khi đọc các số tự nhiên ta đọc từ hàng cao tới hàng thấp, hay từ trái sang phải.
- Để xác định giá trị của chữ số ta cần xác định hàng của chúng. Các chữ số của một số theo thứ tự từ phải sang trái lần lượt là hàng đơn vị, hàng chục, hàng trăm, hàng nghìn, hàng chục nghìn, ....
Lời giải chi tiết:
a) Số \(975 \;368\) đọc là: Chín trăm bảy mươi lăm nghìn ba trăm sáu mươi tám.
Số \(6\; 020\; 975\) đọc là: Sáu triệu không trăm hai mươi nghìn chín trăm bảy mươi lăm.
Số \(94\; 351\; 708\) đọc là: Chín mươi bốn triệu ba trăm năm mươi mốt nghìn bảy trăm linh tám.
Số \(80\; 060\; 090\) đọc là: Tám chục triệu không trăm sáu mươi nghìn không trăm chín mươi.
b) Trong số \(975 \;368\), chữ số \(9\) ở hàng trăm nghìn và có giá trị là \(900\;000\).
Trong số \(6\; 020\; 975\), chữ số \(9\) ở hàng trăm và có giá trị là \(900\).
Trong số \(94\; 351\; 708\), chữ số \(9\) ở hàng chục triệu và có giá trị là \(90\;000\;000\).
Trong số \(80\; 060\; 090\), chữ số \(9\) ở hàng chục và có giá trị là \(90\)..
Bài 2
Đặt tính rồi tính:
a) \(24 579 + 438 67\) b) \(235 \times 325\)
\(82604 - 35246\) \(101598 : 287\)
Phương pháp giải:
Đặt tính rồi tính theo các quy tắc đã học.
Lời giải chi tiết:
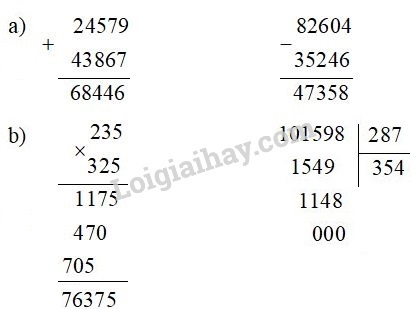
Bài 3
Điền dấu thích hợp (>; <; =) vào chỗ chấm:
\(\dfrac{5}{7} ...\dfrac{7}{9}\) \(\dfrac{7}{8} ... \dfrac{5}{6}\)
\(\dfrac{10}{15} ... \dfrac{16}{24}\) \(\dfrac{19}{43} ... \dfrac{19}{34}\)
Phương pháp giải:
Muốn so sánh hai phân số khác mẫu số ta quy đồng mẫu số hai phân số rồi so sánh hai phân số sau khi quy đồng.
Lời giải chi tiết:
+) Ta có: \(\dfrac{5}{7}= \dfrac{45}{63}\;;\quad \dfrac{7}{9}=\dfrac{49}{63}\).
Mà \( \dfrac{45}{63}< \dfrac{49}{63}\).
Vậy: \(\dfrac{5}{7} <\dfrac{7}{9}\)
+) Ta có: \(\dfrac{7}{8}= \dfrac{21}{24}\;;\quad \dfrac{5}{6}=\dfrac{20}{24}\).
Mà \( \dfrac{21}{24}> \dfrac{20}{24}\).
Vậy: \(\dfrac{7}{8} > \dfrac{5}{6}\)
+) Ta có: \(\dfrac{10}{15}=\dfrac{10:5}{15:5}=\dfrac{2}{3};\) \( \dfrac{16}{24}=\dfrac{16:8}{24:8}=\dfrac{2}{3}\).
Vậy: \(\dfrac{10}{15} = \dfrac{16}{24}\)
+) \(\dfrac{19}{43} < \dfrac{19}{34}\) (vì \(43>34\))
Bài 4
Một thửa ruộng hình chữ nhật có chiều dài \(120m\), chiều rộng bằng \(\dfrac{2}{3}\) chiều dài. Người ta cấy lúa ở đó, tính ra cứ \(100m^2\) thu hoạch được \(50 kg\) thóc. Hỏi đã thu hoạch được ở thửa ruộng đó bao nhiêu tạ thóc ?
Phương pháp giải:
- Tính chiều rộng = chiều dài \(\times \,\dfrac{2}{3}\).
- Tính diện tích = chiều dài \(\times\) chiều rộng.
- Số thóc thu được = số thóc thu được ở \(100m^2\) \(\times\) tỉ số của diện tích và \(100m^2\).
- Đổi kết quả vừa tìm được sang đơn vị đo là tạ, lưu ý \(1\) tạ \(=100kg\).
Lời giải chi tiết:
Tóm tắt
Thửa ruộng hình chữ nhật
Chiều dài: 120m
Chiều rộng: \(\dfrac{2}{3}\) chiều dài
\(100m^2\): \(50 kg\) thóc
Thửa ruộng: ... tạ thóc?
Bài giải
Chiều rộng của thửa ruộng là:
\(120 \times \dfrac{2}{3}=80\;(m)\)
Diện tích của thửa ruộng là:
\(120 \times 80 = 9600\;(m^2)\)
Số tạ thóc thu hoạch được từ thửa ruộng là:
\(50 \times (9600 : 100) = 4800 \;(kg)\)
\(4800 kg = 48\) tạ
Đáp số: \(48\) tạ thóc.
Bài 5
Thay chữ \(a, b\) bằng chữ số thích hợp:

Phương pháp giải:
Dựa vào phép tính đã cho lập luận để tìm các chữ số thích hơp.
Lời giải chi tiết:
a) • \(b\) khác \(0\), vì nếu \(b = 0\) thì \(0\) trừ \(0\) bằng \(0\) (khác \(7\)).
• Do đó phải lấy \(10 - b = 7\), vậy \(b = 3\), nhớ \(1\) sang \(a\).
• \(b\) trừ \(a + 1\) bằng \(0\) nên \(a+1=b\), hay \(a + 1 = 3\) hay \(a = 2\).
Ta có phép tính:
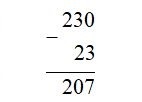
b) • Hàng đơn vị : \(0+b = 8\) nên \(b = 8\).
• Hàng chục : \(8+a = 14\) nên \(a = 6\) (nhớ \(1\)).
• Hàng trăm : \(6\) nhớ \(1\) bằng \(7\) (đúng)
Ta có phép tính: