Bài 1, 2, 3 trang 104 SGK Toán 4
Bài 1: Tính diện tích mỗi hình bình hành sau.
Bài 1
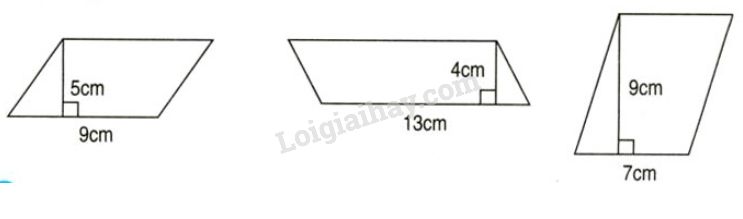
Tính diện tích mỗi hình bình hành sau :
Phương pháp giải:
Diện tích hình bình hành bằng độ dài đáy nhân với chiều cao (cùng một đơn vị đo).
S = a × h
(S là diện tích, a là độ dài cạnh đáy, h là chiều cao hình bình hành).
Lời giải chi tiết:
Hình bình hành bên trái có diện tích là:
9 × 5 = 45 (cm 2 )
Hình bình hành ở giữa có diện tích là:
13 × 4 = 52 (cm 2 )
Hình bình hành bên phải có diện tích là:
7 x 9 = 63 (cm 2 )
Bài 2
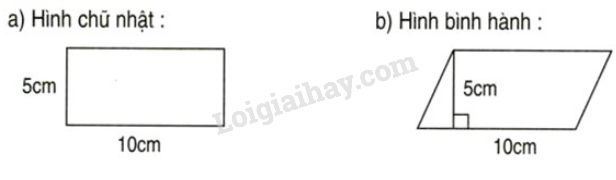
Tính diện tích của :
Phương pháp giải:
Diện tích hình bình hành bằng độ dài đáy nhân với chiều cao (cùng một đơn vị đo).
S = a × h
(S là diện tích, a là độ dài cạnh đáy, h là chiều cao hình bình hành).
Lời giải chi tiết:
Diện tích hình chữ nhật là :
10 × 5 = 50 (cm 2 )
Diện tích hình bình hành là :
10 × 5 = 50 (cm 2 )
Nhận xét : Hình chữ nhật và hình bình hành đã cho có diện tích bằng nhau.
Bài 3
Tính diện tích hình bình hành, biết :
a) Độ dài đáy là 4dm, chiều cao là 34cm.
b) Độ dài đáy là 4m, chiều cao là 13dm.
Phương pháp giải:
Diện tích hình bình hành bằng độ dài đáy nhân với chiều cao (cùng một đơn vị đo).
S = a × h
(S là diện tích, a là độ dài cạnh đáy, h là chiều cao hình bình hành).
Lời giải chi tiết:
a) Đổi : 4dm = 40cm.
Diện tích của hình bình hành là :
40 × 34 = 1360 (cm 2 )
b) Đổi : 4m = 40dm.
Diện tích của hình bình hành là :
40 × 13 = 520 (dm 2 )
Đáp số: a) 1360 cm 2
b) 520 dm 2
Lý thuyết
Diện tích hình bình hành
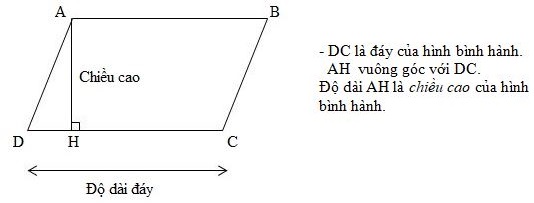
- Cắt phần hình tam giác ADH rồi ghép như hình vẽ để được hình chữ nhật ABIH.
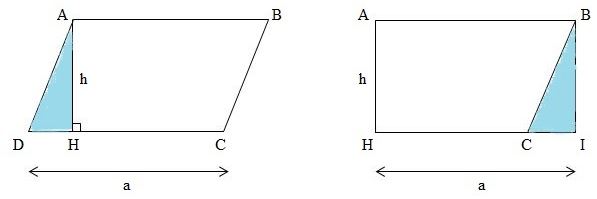
Diện tích hình bình hành ABCD bằng diện tích hình chữ nhật ABIH.
Diện tích hình chữ nhật ABIH là \(a \times h\).
Vậy diện tích hình bình hành ABCD là \(a \times h\).
Diện tích hình bình hành bằng độ dài đáy nhân với chiều cao (cùng một đơn vị đo).
\(S\,= \,a \times h\)
(\(S\) là diện tích, \(a\) là độ dài đáy, \(h\) là chiều cao của hình bình hành).