Bài 1 trang 119 SGK Toán 11 tập 1 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Trong mặt phẳng $\left( P \right)$ cho hình bình hành $ABCD$. Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với $\left( P \right)$ lần lượt đi qua các điểm $A,B,C,D$. Một mặt phẳng $\left( Q \right)$ cắt bốn nửa đường thẳng nói trên tại $A',B',C',D'$. Chứng minh rằng:

$AA' + CC' = BB' + DD'$.

Lời giải chi tiết

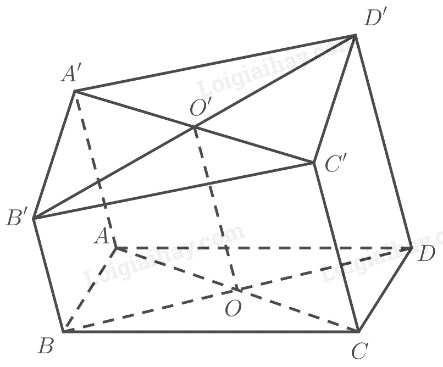
a) Ta có:

$\left. \begin{array}{l}AA'\parallel DD'\\DD' \subset \left( {CC'D'D} \right)\end{array} \right\} \Rightarrow AA'\parallel \left( {CC'D'D} \right)$

$\left. \begin{array}{l}AB\parallel C{\rm{D}}\\C{\rm{D}} \subset \left( {CC'D'D} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {CC'D'D} \right)$

$\left. \begin{array}{l}AA'\parallel \left( {CC'D'D} \right)\\AB\parallel \left( {CC'D'D} \right)\\AA',AB \subset \left( {AA'B'B} \right)\end{array} \right\} \Rightarrow \left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)$

$\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( P \right) \cap \left( {AA'B'B} \right) = A'B'\\\left( P \right) \cap \left( {CC'D'D} \right) = C'D'\end{array} \right\} \Rightarrow A'B'\parallel C'D'\left( 1 \right)$

$\left. \begin{array}{l}AD\parallel BC\\BC \subset \left( {BB'C'C} \right)\end{array} \right\} \Rightarrow AD\parallel \left( {BB'C'C} \right)$

$\left. \begin{array}{l}AA'\parallel BB'\\BB' \subset \left( {BB'C'C} \right)\end{array} \right\} \Rightarrow AA'\parallel \left( {BB'C'C} \right)$

$\left. \begin{array}{l}AA'\parallel \left( {BB'C'C} \right)\\AD\parallel \left( {BB'C'C} \right)\\AA',AD \subset \left( {AA'D'D} \right)\end{array} \right\} \Rightarrow \left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)$

$\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( P \right) \cap \left( {AA'D'D} \right) = A'D'\\\left( P \right) \cap \left( {BB'C'C} \right) = B'C'\end{array} \right\} \Rightarrow A'D'\parallel B'C'\left( 2 \right)$

Từ (1) và (2) suy ra $A'B'C'D'$ là hình bình hành.

Gọi $O = AC \cap B{\rm{D}},O' = A'C' \cap B'{\rm{D}}'$

$\Rightarrow O$ là trung điểm của $AC,B{\rm{D}}$, $O'$ là trung điểm của $A'C',B'{\rm{D}}'$.

$\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( {AA'C'C} \right) \cap \left( {AA'B'B} \right) = AA'\\\left( {AA'C'C} \right) \cap \left( {CC'D'D} \right) = CC'\end{array} \right\} \Rightarrow AA'\parallel CC'$

$\Rightarrow AA'C'C$ là hình thang

$O$ là trung điểm của $AC$

$O'$ là trung điểm của $A'C'$

$\Rightarrow OO'$ là đường trung bình của hình thang $AA'C'C$

$\Rightarrow AA' + CC' = 2OO'\left( 3 \right)$

$\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( {BB'D'D} \right) \cap \left( {AA'B'B} \right) = BB'\\\left( {BB'D'D} \right) \cap \left( {CC'D'D} \right) = DD'\end{array} \right\} \Rightarrow BB'\parallel DD'$

$\Rightarrow BB'D'D$ là hình thang

$O$ là trung điểm của $B{\rm{D}}$

$O'$ là trung điểm của $B'D'$

$\Rightarrow OO'$ là đường trung bình của hình thang $BB'D'D$

$\Rightarrow BB' + DD' = 2OO'\left( 4 \right)$

Từ (3) và (4) suy ra $AA' + CC' = BB' + DD'\left( { = 2OO'} \right)$.