Bài 4.11 trang 100 SGK Toán 11 tập 1 - Cùng khám phá
Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi M, N lần lượt là trọng tâm của các tam giác SAB, SAD. Lấy I là trung điểm của đoạn BC.
Đề bài
Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi M, N lần lượt là trọng tâm của các tam giác SAB, SAD. Lấy I là trung điểm của đoạn BC.
a) Chứng minh rằng MN // BD.
b) Gọi L, H lần lượt là giao điểm của SB, SD với mặt phẳng (MNI). Chứng minh rằng LH // BD.
Phương pháp giải - Xem chi tiết
a) Áp dụng định lý: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
b) - Cách tìm giao điểm của một đường thẳng a với một mặt phẳng (P):
+ Bước 1: Tìm \(\left( Q \right) \supset a\). Tìm \(d = \left( P \right) \cap \left( Q \right)\)
+ Bước 2: Tìm \(I = a \cap d\). I chính là giao điểm của a và (P).
- Áp dụng hệ quả: Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó
Lời giải chi tiết
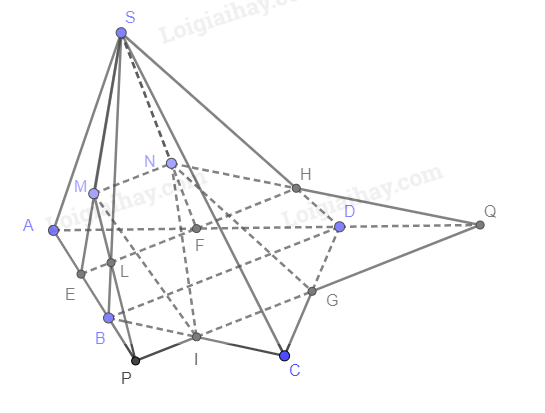
a) Gọi E là trung điểm của AB, F là trung điểm AD
\( \Rightarrow SM = \frac{2}{3}SE,SN = \frac{2}{3}SF\)
Xét tam giác SEF có: \(\frac{{SM}}{{SE}} = \frac{{SN}}{{SF}} = \frac{2}{3} \Rightarrow MN/EF\)
Xét tam giác ABD có E, F lần lượt là trung điểm của AB, AD nên \(EF//BD\)
Vậy \(MN//BD\).
b) Trong (ABCD), gọi \(G\left( {G \in CD} \right)\) sao cho \(IG//BD\), gọi \(P = AB \cap IG,Q = AD \cap IG\).
Mở rộng (MNI) thành (MNQP)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}M \in SE \subset \left( {SAB} \right)\\P \in AB \subset \left( {SAB} \right)\end{array} \right. \Rightarrow MP \subset \left( {SAB} \right)\\MP \subset \left( {MNQP} \right)\\ \Rightarrow MP = \left( {SAB} \right) \cap \left( {MNQP} \right)\end{array}\)
Gọi \(L = SB \cap MP\)\( \Rightarrow L = SB \cap \left( {MNQP} \right)\)(1)
\(\begin{array}{l}\left\{ \begin{array}{l}N \in SF \subset \left( {SAD} \right)\\Q \in AD \subset \left( {SAD} \right)\end{array} \right. \Rightarrow NQ \subset \left( {SAD} \right)\\NQ \subset \left( {MNQP} \right)\\ \Rightarrow NQ = \left( {SAD} \right) \cap \left( {MNQP} \right)\end{array}\)
Gọi \(H = SD \cap NQ\)\( \Rightarrow H = SD \cap \left( {MNQP} \right)\)(2)
Từ (1) và (2) suy ra \(LH = \left( {SBD} \right) \cap \left( {MNQP} \right)\)
Mà \(BD//MN\) (phần a)
\( \Rightarrow LH//BD//MN\).