Bài 4.6 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SCD.
Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SCD.
a) Tim giao tuyến của hai mặt phẳng (SBG) và (SAC).
b) Tìm giao điểm của đường thằng BG và mặt phẳng (SAC).
Phương pháp giải - Xem chi tiết
a) Tìm giao tuyến của hai mặt phẳng (P) và (Q)
Tìm 2 điểm chung A, B của 2 mặt phẳng đó. AB chính là giao tuyến của (P) và (Q).
b) Tìm giao điểm của đường thẳng d và mặt phẳng (P)
Cách 1: Nếu (P) có chứa đường thẳng cắt d
Cách 2: Nếu (P) không chứa đường thẳng cắt d
+ Bước 1: Tìm \(\left( Q \right) \supset d\) và \(\left( P \right) \cap \left( Q \right) = a\)
+ Bước 2: Tìm \(I = a \cap d \Rightarrow I = d \cap \left( P \right)\)
Lời giải chi tiết
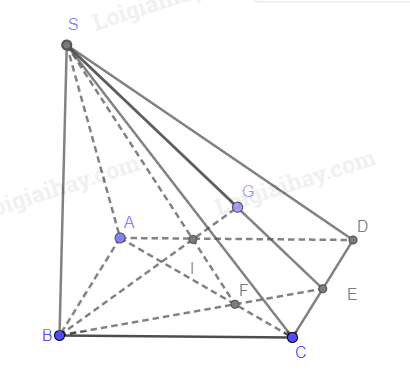
a) Gọi E là trung điểm của CD
Mà G là trọng tâm tam giác SCD nên G nằm trên SE.
Mở rộng (SBG) thành (SBE)
Trong (ABCD), gọi \(AC \cap BE = F\)
\(\begin{array}{l}\left\{ \begin{array}{l}AC \subset \left( {SAC} \right)\\BE \subset \left( {SBE} \right)\end{array} \right.\\ \Rightarrow F \in \left( {SAC} \right) \cap \left( {SBE} \right)\end{array}\)
\(\begin{array}{l} \Rightarrow SF = \left( {SAC} \right) \cap \left( {SBE} \right)\\ \Rightarrow SF = \left( {SAC} \right) \cap \left( {SBG} \right)\end{array}\)
b) Trong (SBE), gọi \(SF \cap AC = I\)
Mà: \(\left\{ \begin{array}{l}\left( {SAC} \right) \cap \left( {SBG} \right) = SF\\AC \subset \left( {SAC} \right)\end{array} \right. \Rightarrow I = BG \cap \left( {SAC} \right)\)