Bài 4.3 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Cho bốn điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AB, CD.
Đề bài
Cho bốn điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AB, CD.
a) Tìm giao tuyến của hai mặt phẳng (ABN) và (MCD).
b) Gọi I và K lần lượt là điểm trên đoạn thẳng AC và AD. Tìm giao tuyến của hai mặt phẳng (MCD) và (BIK).
Phương pháp giải - Xem chi tiết
Tìm giao tuyến của hai mặt phẳng (P) và (Q)
Tìm 2 điểm chung A, B của 2 mặt phẳng đó. AB chính là giao tuyến của (P) và (Q).
Chú ý: Thường tìm 2 đường thẳng đồng phẳng lần lượt nằm trong (P) và (Q). Nếu chúng cắt nhau tại 1 điểm thì đó là điểm chung của (P) và (Q).
Lời giải chi tiết
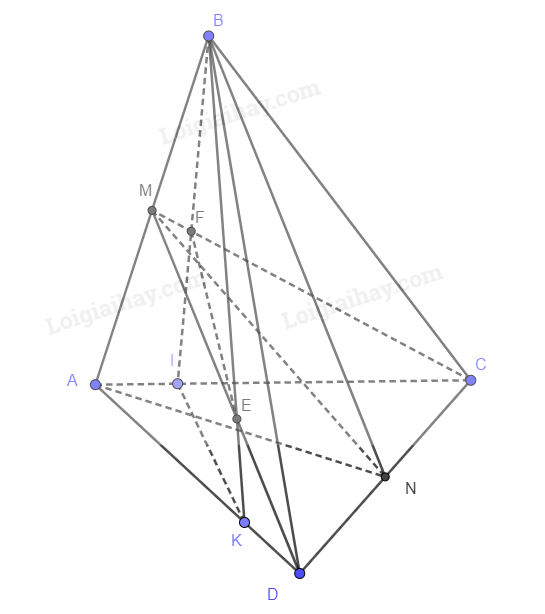
a)
\(\begin{array}{l}\left\{ \begin{array}{l}M \in AB\\AB \subset \left( {ABN} \right)\end{array} \right. \Rightarrow M \in \left( {ABN} \right)\\\left\{ \begin{array}{l}N \in CD\\CD \subset \left( {MCD} \right)\end{array} \right. \Rightarrow N \in \left( {MCD} \right)\\ \Rightarrow \left( {ABN} \right) \cap \left( {MCD} \right) = MN\end{array}\)
b)
\(\begin{array}{l}\left\{ \begin{array}{l}MD \cap BK = E\\MD \subset \left( {MCD} \right)\\BK \subset \left( {BIK} \right)\end{array} \right. \Rightarrow E \in \left( {MCD} \right) \cap \left( {BIK} \right)\\\left\{ \begin{array}{l}MC \cap BI = F\\MC \subset \left( {MCD} \right)\\BI \subset \left( {BIK} \right)\end{array} \right. \Rightarrow F \in \left( {MCD} \right) \cap \left( {BIK} \right)\\ \Rightarrow EF = \left( {MCD} \right) \cap \left( {BIK} \right)\end{array}\)