Bài 4.24 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức
Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm ({A_1},{A_2})sao cho (A{A_1} = {A_1}{A_2} = {A_2}S.) Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua ({A_1},{A_2}.) Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại ({B_1},{C_1}.) Mặt phẳng (Q) cắt các canhj SB, SC lần lượt tại ({B_2},{C_2}.) Chứng minh (B{B_1} = {B_1}{B_2} = {B_2}S) và (C{C_1} = {C_1}{C_2} = {C_2}S).
Đề bài
Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm \({A_1},{A_2}\)sao cho \(A{A_1} = {A_1}{A_2} = {A_2}S.\) Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua \({A_1},{A_2}.\) Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại \({B_1},{C_1}.\) Mặt phẳng (Q) cắt các canhj SB, SC lần lượt tại \({B_2},{C_2}.\) Chứng minh \(B{B_1} = {B_1}{B_2} = {B_2}S\) và \(C{C_1} = {C_1}{C_2} = {C_2}S\).
Phương pháp giải - Xem chi tiết
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
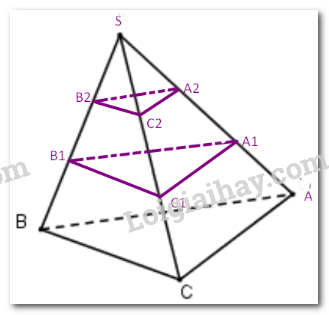
Áp dụng định lí Thales cho ba mặt phẳng ( ABC ), ( P), (Q) và hai cát tuyến SA , SC ta có:
\(\frac{{{C_2}S}}{{{A_2}S}} = \frac{{{C_1}{C_2}}}{{{A_1}{A_{2\;}}}} = \frac{{C{C_1}}}{{A{A_1}}}\) mà \(A{A_1} = {A_1}{A_2} = {A_2}S\).
Suy ra \(C{C_1} = {C_1}{C_2} = {C_2}S\). Áp dụng định lí Thales cho ba mặt phẳng ( ABC), (P), (Q) và hai cát tuyến SA , SB ta có:
\(\frac{{{B_2}S}}{{{A_2}S}} = \frac{{{B_1}{B_2}}}{{{A_1}{A_2}}} = \frac{{B{B_1}}}{{A{A_1}}}\) mà \(A{A_1} = A{A_2} = {A_2}S\).
Suy ra \(B{B_1} = {B_1}{B_2} = {B_2}S\).