Bài 4.19 trang 87 SGK Toán 11 tập 1 - Kết nối tri thức
Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Gọi E là một điểm nằm giữa S và A. Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (P) và các mặt bên của hình chóp. Hình tạo bởi các giao tuyến là hình gì?
Đề bài
Cho hình chóp S.ABCD có đáy là hình thang (AB//CD) . Gọi E là một điểm nằm giữa S và A . Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (P) và các mặt bên của hình chóp. Hình tạo bởi các giao tuyến là hình gì?
Phương pháp giải - Xem chi tiết
Cho đường thẳng a song song với mặt phẳng (P) . Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a.
Lời giải chi tiết
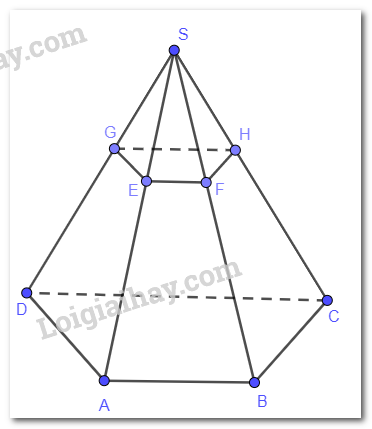
Mặt phẳng ( SAD ) chứa đường thẳng AD song song với mp(P ) nên mặt phẳng ( P) cắt ( SAD ) theo giao tuyến song song với AD . Vẽ EG // AD (G thuộc SD ) thì EG là giao tuyến của ( P ) và ( SAD ).
Mặt phẳng ( SAB ) chứa đường thẳng AB song song với mp(P) nên mặt phẳng (P) cắt ( SAB ) theo giao tuyến song song với AB . Vẽ EF // AB ( F thuộc SB ) thì EF là giao tuyến của ( P ) và ( SAB ).
Ta có AB // CD, EF // AB suy ra CD // EF hay CD // mp(P)
Mặt phẳng ( SCD ) chứa đường thẳng CD song song với mp(P) nên mặt phẳng ( P ) cắt ( SCD ) theo giao tuyến song song với CD . Vẽ GH // CD ( H thuộc SC ) thì GH là giao tuyến của ( P) và ( SCD ).
FH thuộc ( P ), FH thuộc ( SBC ) suy ra FH là giao tuyến của (P ) và ( SBC ).
Tứ giác EFGH có EF // GH (vì cùng song song với CD ) suy ra EFGH là hình thang.