Bài 5 trang 106 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho hình chóp (S.ABCD) có đáy là hình bình hành, (AC) và (BD) cắt nhau tại (O). Gọi (I) là trung điểm của (SO). Mặt phẳng (left( {ICD} right)) cắt (SA,SB) lần lượt tại (M,N).
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, \(AC\) và \(BD\) cắt nhau tại \(O\). Gọi \(I\) là trung điểm của \(SO\). Mặt phẳng \(\left( {ICD} \right)\) cắt \(SA,SB\) lần lượt tại \(M,N\).
a) Hãy nói cách xác định hai điểm \(M\) và \(N\). Cho \(AB = a\). Tính \(MN\) theo \(a\).
b) Trong mặt phẳng \(\left( {CDMN} \right)\), gọi \(K\) là giao điểm của \(CN\) và \(DM\). Chứng minh \(SK\parallel BC\parallel AD\).
Phương pháp giải - Xem chi tiết
a) – Để xác định hai điểm \(M\) và \(N\), ta sử dụng tính chất về giao tuyến của hai mặt phẳng và định lí 2 về giao tuyến của ba mặt phẳng.
– Để tính độ dài đoạn thẳng \(MN\), ta sử dụng định lí Medelaus và định lí Thales.
b) Áp dụng định lí 2 về giao tuyến của ba mặt phẳng.
Lời giải chi tiết
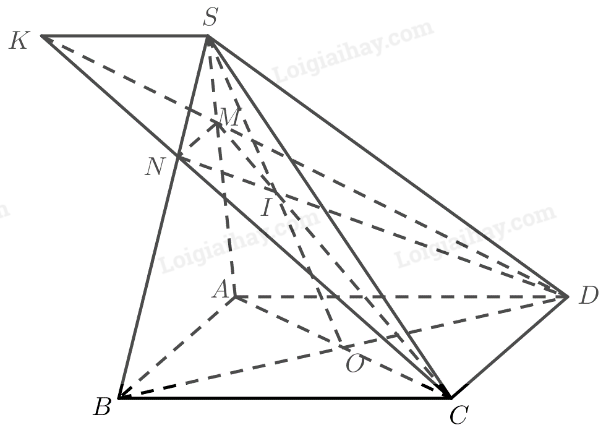
a) • Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {IC{\rm{D}}} \right)\\M \in SA \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow M \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\C \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\end{array}\)
\( \Rightarrow M,I,C\) thẳng hàng.
Do đó \(M\) là giao điểm của \(IC\) và \(SA\).
• Ta có:
\(\begin{array}{l}\left. \begin{array}{l}N \in \left( {IC{\rm{D}}} \right)\\N \in SB \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow N \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\D \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
\( \Rightarrow N,I,D\) thẳng hàng.
Do đó \(N\) là giao điểm của \(I{\rm{D}}\) và \(SB\).
• Ta có:
\(\begin{array}{l}AB = \left( {SAB} \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {IC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN = \left( {SAB} \right) \cap \left( {IC{\rm{D}}} \right)\\AB\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(AB\parallel C{\rm{D}}\parallel MN\).
Áp dụng định lí Medelaus cho tam giác \(SOA\) với cát tuyến \(CIM\), ta có:
\(\frac{{SM}}{{MA}}.\frac{{AC}}{{OC}}.\frac{{OI}}{{SI}} = 1 \Leftrightarrow \frac{{SM}}{{MA}}.2.1 = 1 \Leftrightarrow \frac{{SM}}{{MA}} = \frac{1}{2}\)
Xét tam giác \(SAB\) có \(MN\parallel AB\). Theo định lí Thales ta có:
\(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{1}{3} \Leftrightarrow MN = \frac{1}{3}AB = \frac{a}{3}\)
b) Ta có:
\(\begin{array}{l}BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\SK = \left( {SAD} \right) \cap \left( {SBC} \right)\\AD\parallel BC\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(SK\parallel BC\parallel A{\rm{D}}\).