Bài 6 trang 127 SGK Toán 11 tập 1 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng 10. $M$ là điểm trên $SA$ sao cho $\frac{{SM}}{{SA}} = \frac{2}{3}$. Một mặt phẳng $\left( \alpha  \right)$ đi qua $M$ song song với $AB$ và $C{\rm{D}}$, cắt hình chóp theo một tứ giác có diện tích là

A. $\frac{{400}}{9}$.

B. $\frac{{200}}{3}$.

C. $\frac{{40}}{9}$.

D. $\frac{{200}}{9}$.

Lời giải chi tiết

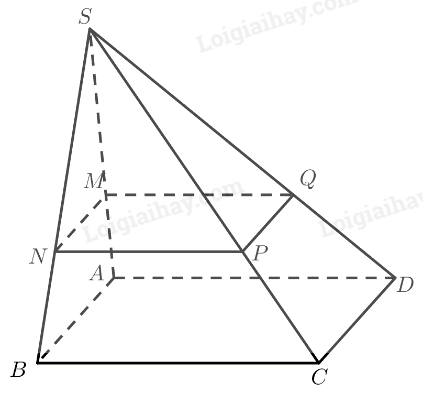
Qua $M$ dựng đường thẳng song song với $AB$, cắt $SB$ tại $N$.

Qua $N$ dựng đường thẳng song song với $BC$, cắt $SC$ tại $P$.

Qua $M$ dựng đường thẳng song song với $AD$, cắt $SD$ tại $Q$.

Ta có:

$\left. \begin{array}{l}MN\parallel AB\\AB \subset \left( {ABCD} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {ABCD} \right)$

$\left. \begin{array}{l}MQ\parallel AD\\AD \subset \left( {ABCD} \right)\end{array} \right\} \Rightarrow MQ\parallel \left( {ABCD} \right)$

$\left. \begin{array}{l}MN\parallel \left( {ABCD} \right)\\MQ\parallel \left( {ABCD} \right)\\MN,MQ \subset \left( \alpha  \right)\end{array} \right\} \Rightarrow \left( {MNPQ} \right)\parallel \left( {ABCD} \right)$

$\Rightarrow \frac{{{S_{MNPQ}}}}{{{S_{ABC{\rm{D}}}}}} = {\left( {\frac{{MN}}{{AB}}} \right)^2}$

Ta có: ${S_{ABC{\rm{D}}}} = A{B^2} = {10^2} = 100$

$MN\parallel AB \Rightarrow \frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}$

$\Rightarrow \frac{{{S_{MNPQ}}}}{{{S_{ABC{\rm{D}}}}}} = {\left( {\frac{2}{3}} \right)^2} = \frac{4}{9} \Rightarrow {S_{MNPQ}} = \frac{4}{9}{S_{ABC{\rm{D}}}} = \frac{4}{9}.100 = \frac{{400}}{9}$

Chọn A.