Bài 9 trang 171 Tài liệu dạy – học Toán 7 tập 1 — Không quảng cáo

Đề bài

Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm N sao cho BM = CN.

a) Tam giác AMN là tam giác gì ? Vì sao ?

b) Kẻ $BH \bot AM(H \in AM)$  kẻ $CK \bot AN(K \in AN).$  Chứng minh rằng BH = CK. Tam giác OBC là tam giác gì ? Vì sao ?

Lời giải chi tiết

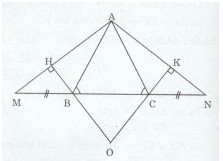
a)Ta có: $\eqalign{  & \widehat {ABM} + \widehat {ABC} = {180^0}  \cr  & \widehat {ACN} + \widehat {ACB} = {180^0} \cr}$  (kề bù)

Suy ra $\widehat {ABM} + \widehat {ACB} = \widehat {ACN} + \widehat {ACB}$

Mà $\widehat {ABC} = \widehat {ACB}(\Delta ABC$  cân tại A)

Nên $\widehat {ABM} = \widehat {ACN}$

Xét tam giác ABM và CAN ta có:

AB = AC (tam giác ABC cân tại A)

BM = CN (giả thiết)

$\widehat {ABM} = \widehat {ACN}(cmt)$

Do đó: $\Delta ABM = \Delta ACN(c.g.c) \Rightarrow AM = AN.$

Vậy tam giác AMN cân tại A.

b) Xét tam giác MBH vuông tại H và tam giác NCK vuông tại K ta có:

MB = CN (giả thiết)

$\widehat {BMH} = \widehat {CNK}(\Delta AMN$  cân tại A)

Do đó: $\Delta MBH = \Delta NCK$  (cạnh huyền - góc nhọn) => BH = CK.

c) Ta có: $\eqalign{  & \widehat {MBH} = \widehat {OBC}  \cr  & \widehat {KCN} = \widehat {OCB} \cr}$  (hai góc đối đỉnh)

Mà $\widehat {MBH} = \widehat {KCN}(\Delta MBH = \Delta NCK) \Rightarrow \widehat {OBC} = \widehat {OCB}$

Vậy tam giác OBC cân tại O.