Bài 8 trang 171 Tài liệu dạy – học Toán 7 tập 1 — Không quảng cáo

Đề bài

Cho tam giác ABC nhọn (AB < AC). Kẻ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh rằng \(\Delta ABH = \Delta MBH.\)

b) Chứng minh rằng \(\widehat {BAC} = \widehat {BMC}.\)

c) Gọi I là trung điểm của BC. Trên tia đối của tia IA lấy điểm N sao cho I là trung điểm của AN. Chứng minh rằng NC = BM.

d) Cho AB = 13 cm, AH = 12 cm, HC = 16 cm. Tính độ dài của cạnh AC, BC.

Lời giải chi tiết

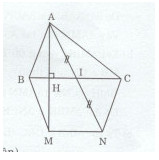
a)Xét hai tam giác ABH và MBH ta có:

\(\widehat {AHB} = \widehat {MHB}( = {90^0})\)

AH = MH (H là trung điểm của AM)

BH là cạnh chung.

Do đó: \(\Delta ABH = \Delta MBH(c.g.c)\)

b) Ta có: \(\Delta ABH = \Delta MBH\)  (chứng minh câu a)

Suy ra: AB = MB và \(\widehat {ABH} = \widehat {MBH}.\)

Xét hai tam giác ABC và MBC ta có:

BC là cạnh chung

\(\widehat {ABC} = \widehat {MBC}(cmt)\)

AB = BM (chứng minh trên)

Do đó: \(\Delta ABC = \Delta MBC(c.g.c) \Rightarrow \widehat {BAC} = \widehat {BMC}.\)

c) Xét tam giác ABI và NCI ta có:

AI = NI (I là trung điểm của AN)

\(\widehat {AIB} = \widehat {CIN}\)   (hai góc đối đỉnh)

BI = CI (I là trung điểm của BC)

Do đó: \(\Delta ABI = \Delta NCI(c.g.c) \Rightarrow AB = CN.\)

Mà AB = BM (chứng minh câu b) nên CN = BM.

d) Tam giác ABH vuông tại H \(\Rightarrow B{H^2} + A{H^2} = A{B^2}\)  (định lí Pythagore)

\(B{H^2} = A{B^2} - A{H^2} = {13^2} - {12^2} = 169 - 144 = 25.\)

Mà BH > 0. Do đó: \(BH = \sqrt {25}  = 5(cm).\)

Tam giác AHC vuông tại H \(\Rightarrow A{C^2} = A{H^2} + H{C^2}\)   (định lí Pythagore)

Do đó: \(A{C^2} = A{H^2} + H{C^2} = {12^2} + {16^2} = 400.\)

Mà AC > 0 nên \(AC = \sqrt {400}  = 20(cm)\)

Mặt khác BC = BH + HC = 5 + 16 = 21 (cm).