Bài tập 1 trang 151 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Tìm số đo x, y ở các hình 37a, b, c, d, e, f
Đề bài
Tìm số đo x, y ở các hình 37a, b, c, d, e, f
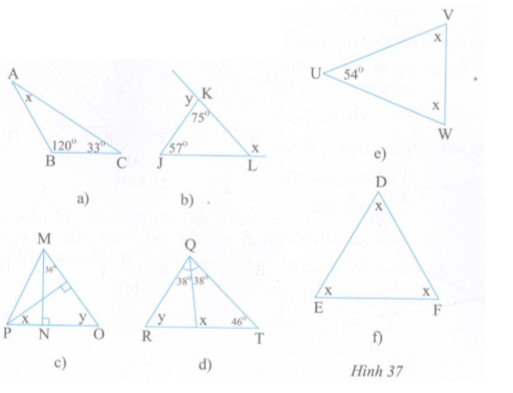
Phương pháp giải - Xem chi tiết
- Tổng 3 góc trong tam giác bằng \(180^{0}\)
- Góc ngoài tam gíac bằng tổng 2 góc trong không kề với nó
Lời giải chi tiết
a)Tam giác ABC có: \(\widehat A + \widehat B + \widehat C = {180^0}\)
Do đó: \(x + {120^0} + {33^0} = {180^0} \Rightarrow x = {180^0} - {120^0} - {33^0} = {27^0}\)
b) \(y + {75^0} = {180^0}\) (hai góc kề bù) \( \Rightarrow x = {75^0} + {57^0} = {132^0}\)
\(x = \widehat {JKL} + \widehat {KJL}\) (góc ngoài của tam giác KJL)
\(\rightarrow x = {75^0} + {57^0} = {132^0}\)
c) Tam giác MNO có: \(\widehat {MNO} + \widehat {NMO} + \widehat {MON} = {180^0}\)
Do đó: \({90^0} + {36^0} + \widehat {MON} = {180^0} \)
\(\Rightarrow \widehat {MON} = y = {180^0} - {90^0} - {36^0} = {54^0}\)
\(x + {90^0} + y = {180^0}\) (tổng ba góc trong một tam giác)
\(\Rightarrow x = {180^0} - {90^0} - {54^0} = {36^0}\)
d) Tam giác RQT có: \(\widehat {RQT} + \widehat {QTR} + \widehat {QRT} = {180^0}\)
Do đó: \({38^0} + {38^0} + {46^0} + y = {180^0} \)
\(\Rightarrow y = {180^0} - {38^0} - {38^0} - {46^0} = {58^0}\)
\(x = y + {38^0}\) (góc ngoài của tam giác) \( \Rightarrow x = {58^0} + {38^0} = {96^0}\)
e) Tam giác UVW có:\(\widehat U + \widehat V + \widehat {\rm{W}} = {180^0}\)
Do đó: \({54^0} + x + x = {180^0} \Rightarrow 2x = {180^0} - {54^0} = {126^0}\)
\(\Rightarrow x = {{{{126}^0}} \over 2} = {63^0}\)
f) Tam giác DEF có: \(\widehat D + \widehat E + \widehat F = {180^0}\)
Do đó: \(x + x + x = {180^0} \Leftrightarrow 3x = {180^0} \Rightarrow x = {{{{180}^0}} \over 3} = {60^0}\)