Bài tập 13 trang 96 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho hình vẽ sau:
Đề bài
Cho hình vẽ sau:
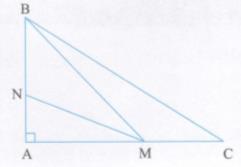
Hãy chứng minh rằng:
a) BM < BC
b) MN < BC
Lời giải chi tiết
a) Ta có AM, AC lần lượt là hình chiếu của đường xiên BM, BC trên đường thẳng AC và AM < AC (vì \(M \in AC\)).
=> BM < BC (quan hệ giữa hình chiếu và đường xiên).
b) Ta có \(\widehat {BNM}\) là góc ngoài của ∆ANM nên \(\widehat {BNM} > \widehat {NAM}.\)
Mà \(\widehat {NAM} = 90^\circ\) (gt) nên \(\widehat {BNM} > 90^\circ\) hay \(\widehat {BNM}\) tù
∆BNM có \(\widehat {BNM}\) tù nên MN < BM
Mặt khác BM < BC nên MN < BM < BC
Cùng chủ đề:
Bài tập 13 trang 96 Tài liệu dạy – học Toán 7 tập 2