Bài tập 13 trang 122 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC cân tại A. Tia phân giác của góc B và C gặp nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC.
Đề bài
Cho tam giác ABC cân tại A. Tia phân giác của góc B và C gặp nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC.
Lời giải chi tiết
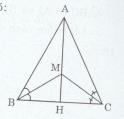
∆ABC có M là giao điểm của hai đường phân giác xuất phát từ B và C (gt)
Nên theo định lý về ba đường phân giác của tam giác, ta có:
M là điểm cách đều ba cạnh của tam giác ABC.
=> AM là tia phân giác của \(\widehat {BAC}\)
∆ABC cân tại A có AH là đường phân giác
=> AH cũng là đường trung tuyến
Vậy H là trung điểm của BC.
Cùng chủ đề:
Bài tập 13 trang 122 Tài liệu dạy – học Toán 7 tập 2