Bài tập 15 trang 122 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác AMN vuông tại A. Tia phân giác của góc M và N gặp nhau tại I. Tia MI cắt AN tại R. Kẻ RT vuông góc với AI . Chứng minh rằng AT = RT.
Đề bài
Cho tam giác AMN vuông tại A. Tia phân giác của góc M và N gặp nhau tại I. Tia MI cắt AN tại R. Kẻ RT vuông góc với AI (\(T \in AI\) ). Chứng minh rằng AT = RT.
Lời giải chi tiết
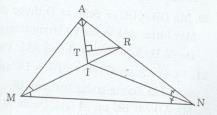
∆ABC có: I là giao điểm của hai đường phân giác của góc M và N (gt)
Do đó: theo định lí về ba đường phân giác ta có I là điểm cách đều ba cạnh của tam giác ABC.
=> AI là tia phân giác của \(\widehat {MAN}\)
Do đó \(\widehat {RAI} = {{\widehat {MAN}} \over 2} = {{90^\circ } \over 2} = 45^\circ\)
Ta có ∆ART vuông tại T có \(\widehat {RAT} = 45^\circ\)
Do đó ∆ART vuông cân tại T => AT = RT.
Cùng chủ đề:
Bài tập 15 trang 122 Tài liệu dạy – học Toán 7 tập 2