Bài tập 19 trang 129 Tài liệu dạy – học Toán 7 tập 1 — Không quảng cáo

Đề bài

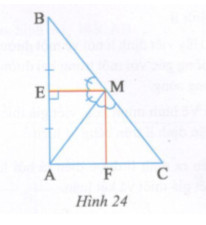
Cho hình 24, biết E là trung điểm của AB; ME vuông góc với AB tại E và ME, MF lần lượt là tia phân giác của $\widehat {ABM};\,\,\,\widehat {AMC}$

a) Vì sao EM là đường trung trực của đoạn thẳng AB ?

b) Chứng tỏ rằng MF // AB.

Lời giải chi tiết

a) Ta có: $ME \bot AB$ tại E (giả thiết) và E là trung điểm AB (giả thiết)

Do đó ME là đường trung trực của AB.

b) $\widehat {AME} = {1 \over 2}\widehat {AMB}$  (ME là tia phân giác của góc AMB)

$\widehat {{\rm{AMF}}} = {1 \over 2}\widehat {AMC}$  (MF là tia phân giác của góc AMC)

Và $\widehat {AMB} + \widehat {AMC} = {180^0}$  (hai góc kề bù)

Do đó $2\widehat {AME} + 2\widehat {{\rm{AMF}}} = {180^0} \Rightarrow \widehat {AME} + \widehat {{\rm{AMF}}} = {{{{180}^0}} \over 2} = {90^0}$

Mà $\widehat {{\rm{EMF}}} = \widehat {AME} + \widehat {{\rm{AMF}}}.$  Nên $\widehat {{\rm{EMF}}} = {90^0} \Rightarrow MF \bot ME$

Mà $AB \bot ME$  (giả thiết) do đó AB // MF.