Bài tập cuối tuần Toán 4 tuần 24 - Đề 2 (Có đáp án và lời giải chi tiết)
Tải vềBài tập cuối tuần 24 - Đề 2 bao gồm các bài tập chọn lọc với các dạng bài tập giúp các em ôn lại kiến thức đã học trong tuần
Đề bài
Bài 1. Nối mỗi phép tính với kết quả đúng của nó
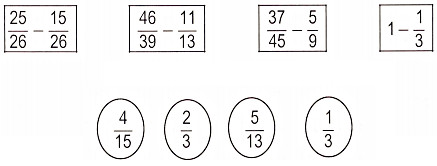
Bài 2: Tính:
a) \(\dfrac{7}{8} - \dfrac{5}{8}\) = ............................................
b) \(\dfrac{5}{6} - \dfrac{3}{8}\) = ............................................
c) \(\dfrac{{11}}{{12}} - \dfrac{3}{4}\) = ...........................................
Bài 3. Tìm \(x\), biết:
\(a)\,\,x - \dfrac{1}{2} = \dfrac{1}{3}\) \(b)\,\,\dfrac{5}{6} - x = \dfrac{3}{8}\)
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 4. Trong công viên có \(\dfrac{3}{4}\) diện tích đã trồng cây xanh và hoa, trong đó có \(\dfrac{1}{3}\) diện tích của công viên là trồng cây xanh. Hỏi diện tích trồng hoa chiếm bao nhiêu phần diện tích công viên ?
Bài giải
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 5 . Một đội công nhân sửa đường. Trong tuần đầu sửa được \(\dfrac{2}{5}\) quãng đường, tuần thứ hai sửa được \(\dfrac{3}{7}\) quãng đường. Hỏi sau hai tuần đội công nhân sửa được mấy phần quãng đường đó ?
Bài giải
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Lời giải chi tiết
Bài 1 .
Phương pháp:
- Muốn trừ hai phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Cách giải:
Ta có:
\(\dfrac{{25}}{{26}} - \dfrac{{15}}{{26}} = \dfrac{{10}}{{26}} = \dfrac{5}{{13}};\) \(\dfrac{{46}}{{39}} - \dfrac{{11}}{{13}} = \dfrac{{46}}{{39}} - \dfrac{{33}}{{39}} = \dfrac{{13}}{{39}} = \dfrac{1}{3};\)
\(\dfrac{{37}}{{45}} - \dfrac{5}{9} = \dfrac{{37}}{{45}} - \dfrac{{25}}{{45}} = \dfrac{{12}}{{45}} = \dfrac{4}{{15}};\) \(1 - \dfrac{1}{3} = \dfrac{3}{3} - \dfrac{1}{3} = \dfrac{2}{3}.\)
Vậy ta có kết quả như sau:
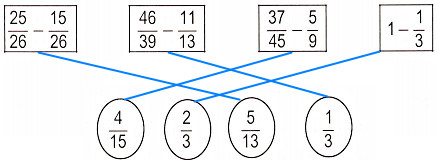
Bài 2 .
Phương pháp:
- Muốn trừ hai phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Cách giải:
a) \(\dfrac{7}{8} - \dfrac{5}{8} = \dfrac{2}{8} = \dfrac{1}{4};\)
b) \(\dfrac{5}{6} - \dfrac{3}{8} = \dfrac{{20}}{{24}} - \dfrac{9}{{24}} = \dfrac{{11}}{{24}};\)
c) \(\dfrac{{11}}{{12}} - \dfrac{3}{4} = \dfrac{{11}}{{12}} - \dfrac{9}{{12}} = \dfrac{2}{{12}} = \dfrac{1}{6}.\)
Bài 3 .
Phương pháp:
Áp dụng các quy tắc:
- Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
- Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
Cách giải:
\(\begin{array}{l}a)\,\,x - \dfrac{1}{2} = \dfrac{1}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{1}{3} + \dfrac{1}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{5}{6}\end{array}\) \(\begin{array}{l}b)\,\,\dfrac{5}{6} - x = \dfrac{3}{8}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{5}{6} - \dfrac{3}{8}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{{11}}{{24}}\end{array}\)
Bài 4 .
Phương pháp:
Muốn tìm diện tích trồng hoa ta lấy diện tích đã trồng hoa và cây xanh trừ đi diện tích đã trồng cây xanh.
Cách giải:
Diện tích trồng hoa chiếm số phần diện tích công viên là:
\(\dfrac{3}{4} - \dfrac{1}{3} = \dfrac{5}{{12}}\) (diện tích công viên)
Đáp số: \(\dfrac{5}{{12}}\) diện tích công viên.
Bài 5 .
Phương pháp:
Muốn tìm số phần quãng đường đội công nhân sửa được trong 2 tuần ta lấy số phần quãng đường sửa được trong tuần đầu cộng với số phần quãng đường sửa được trong tuần thứ hai.
Cách giải:
Sau 2 tuần, đội công nhân sửa được số phần quãng đường là:
\(\dfrac{2}{5} + \dfrac{3}{7} = \dfrac{{29}}{{35}}\) (quãng đường)
Đáp số : \(\dfrac{{29}}{{35}}\) quãng đường.