Bài tập cuối tuần Toán 4 tuần 23 - Đề 1 (Có đáp án và lời giải chi tiết)

Tải về

Bài tập cuối tuần 23 - Đề 1 bao gồm các bài tập chọn lọc với các dạng bài tập giúp các em ôn lại kiến thức đã học trong tuần

Đề bài

Phần I. Trắc nghiệm

Câu 1 . Đúng ghi Đ, sai ghi S vào chỗ chấm

Trong các số 1820 ; 3675 ; 954000 ; 47205 có:

A. Những số chia hết cho cả 2 và 5 là 1820 và 47205 …

B. Những số chia hết cho cả 3 và 5 là 3675 ; 954000 và 47205 …

C. Số chia hết cho 2 nhưng không chia hết cho 5 là 1820 …

D. Số chia hết cho cả 2, 3, 5 và 9 là 954000 …

Câu 2. Quy đồng mẫu số hai phân số \(\dfrac{5}{7}\) và \(\dfrac{4}{9}\) được hai phân số mới là :

A. \(\dfrac{{35}}{{63}}\) và \(\dfrac{{36}}{{63}}\) B. \(\dfrac{{45}}{{63}}\) và \(\dfrac{{28}}{{63}}\)

C. \(\dfrac{{45}}{{20}}\) và \(\dfrac{{28}}{{20}}\) D. \(\dfrac{{35}}{{20}}\) và \(\dfrac{{36}}{{20}}\).

Câu 3. Điền dấu thích hợp vào chỗ chấm:

\(a)\,\,\dfrac{3}{{16}}\,\,.\,..\,\,\dfrac{{13}}{{16}}\) \(b)\,\,\dfrac{{17}}{{15}}\,\,...\,\,\dfrac{{14}}{{15}}\) \(c)\,\,\dfrac{{20}}{{21}}\,\,...\,\,1\)

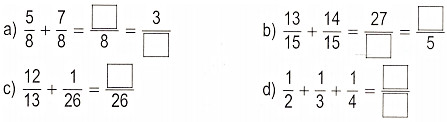
Câu 4. Điền số thích hợp vào ô trống:

Phần II. Trình bày chi tiết các bài toán

Bài 1. Đặt tính rồi tính

a) 4765 + 5279 b) 27563 – 9178

c) 1385 × 304 d) 103530 : 435

........................................................................................................................................

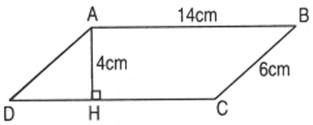
Bài 2. Cho hình bình hành ABCD có AB = 14cm, BC = 6cm và chiều cao AH = 4cm (như hình vẽ). Hãy tính chu vi và diện tích của hình bình hành ABCD.

........................................................................................................................................

Bài 3. Rút gọn rồi tính

\(a)\,\,\dfrac{4}{{16}} + \dfrac{1}{4}\) \(b)\,\,\dfrac{{15}}{{25}} + \dfrac{6}{{10}}\) \(c)\,\,\dfrac{5}{9} + \;\dfrac{{21}}{{28}}\)

........................................................................................................................................

Bài 4. Sơ kết học kì năm học 2007 – 2008 lớp 4A có \(\dfrac{1}{3}\) số học sinh đạt loại giỏi, \(\dfrac{2}{5}\) số học sinh đạt loại khá. Hỏi số học sinh đạt loại khá và giỏi trên chiếm bao nhiêu phần số học sinh của lớp ?

Bài giải

........................................................................................................................................

Lời giải chi tiết

Phần I

Câu 1.

Phương pháp:

Áp dụng dấu hiệu chia hết cho 2, 5, 3, 9:

- Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2.

- Các số có chữ số tận cùng là 0, 5 thì chia hết cho 5.

- Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.

- Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.

- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.

Cách giải:

A. S B. Đ

C. S D. Đ

Câu 2 .

Phương pháp:

Quy đồng mẫu số hai phân số \(\dfrac{5}{7}\) và \(\dfrac{4}{9}\) với mẫu số chung là 63.

Cách giải:

Ta có:

\(\dfrac{5}{7} = \dfrac{{5 \times 9}}{{7 \times 9}} = \dfrac{{45}}{{63}}\,;\) \(\dfrac{4}{9} = \dfrac{{4 \times 7}}{{9 \times 7}} = \dfrac{{28}}{{63}}\,.\)

Vậy quy đồng mẫu số hai phân số \(\dfrac{5}{7}\) và \(\dfrac{4}{9}\) ta được hai phân số là \(\dfrac{{45}}{{63}}\) và \(\dfrac{{28}}{{63}}\).

Chọn B.

Câu 3 .

Phương pháp:

- Trong hai phân số có cùng mẫu số, phân số nào có tử số bé hơn thì bé hơn, phân số nào có tử số lớn hơn thì lớn hơn, nếu tử số bằng nhau thì hai phân số bằng nhau.

- Phân số có tử số nhỏ hơn mẫu số thì nhỏ hơn 1.

Cách giải:

\(a)\,\,\dfrac{3}{{16}}\,\, < \,\,\,\dfrac{{13}}{{16}}\) \(b)\,\,\dfrac{{17}}{{15}}\,\, > \,\,\dfrac{{14}}{{15}}\) \(c)\,\,\dfrac{{20}}{{21}}\,\, < \,\,1\)

Câu 4.

Phương pháp:

- Muốn cộng hai phân số cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.

- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.

Cách giải:

Ta có:

a) \(\dfrac{5}{8} + \dfrac{7}{8} = \dfrac{{12}}{8} = \dfrac{3}{2};\)

b) \(\dfrac{{13}}{{15}} + \dfrac{{14}}{{15}} = \dfrac{{27}}{{15}} = \dfrac{9}{5}\) ;

c) \(\dfrac{{12}}{{13}} + \dfrac{1}{{26}} = \dfrac{{24}}{{26}} + \dfrac{1}{{26}} = \dfrac{{25}}{{26}}\) ;

d) \(\dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} = \dfrac{3}{6} + \dfrac{2}{6} + \dfrac{1}{4}\)\( = \dfrac{5}{6} + \dfrac{1}{4} = \dfrac{{10}}{{12}} + \dfrac{3}{{12}} = \dfrac{{13}}{{12}}\).

Vậy ta điền như sau:

Phần II

Câu 1.

Phương pháp:

- Đặt tính : Viết các chữ số cùng hàng đặt thẳng cột với nhau.

- Tính : Cộng, trừ hoặc nhân lần lượt từ phải sang trái.

Phép chia ta đặt theo cột dọc, sau đó chia lần lượt từ trái sang phải.

Cách giải:

Câu 2.

Phương pháp:

- Muốn tính chu vi hình bình hành ta lấy tổng độ dài của hai cạnh kề nhau (cùng một đơn vị đo) nhân với 2.

- Muốn tính diện tích hình bình hành ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo)

Cách giải:

Chu vi của hình bình hành ABCD là :

(14 + 6) × 2 = 40 (cm)

Diện tích của hình bình hành ABCD là :

14 × 4 = 56 (cm ² )

Đáp số: Chu vi: 40cm;

Diện tích: 56cm ² .

Câu 3.

Phương pháp:

- Rút gọn phân số thành phân số tối giản (nếu được).

- Muốn cộng hai phân số cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.

- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.

Cách giải:

\(\begin{array}{l}a)\,\,\dfrac{4}{{16}} + \dfrac{1}{4} = \dfrac{1}{4} + \dfrac{1}{4} = \dfrac{2}{4} = \dfrac{1}{2};\\b)\,\,\dfrac{{15}}{{25}} + \dfrac{6}{{10}} = \dfrac{3}{5} + \dfrac{3}{5} = \dfrac{6}{5};\end{array}\)

\(c)\,\,\dfrac{5}{9} + \dfrac{{21}}{{28}} = \dfrac{5}{9} + \dfrac{3}{4}\)\( = \dfrac{{20}}{{36}} + \dfrac{{27}}{{36}} = \dfrac{{47}}{{36}}.\)

Câu 4.

Phương pháp:

Tìm phân số chỉ số học sinh đạt loại khá và giỏi ta lấy phân số chỉ số học sinh đạt loại khá cộng với phân số chỉ số học sinh đạt loại giỏi.

Cách giải:

Số học sinh đạt loại khá và giỏi trên chiếm số phần số học sinh của lớp là:

\(\dfrac{1}{3} + \dfrac{2}{5} = \dfrac{{11}}{{15}}\) (số học sinh cả lớp)

Đáp số : \(\dfrac{{11}}{{15}}\) số học sinh cả lớp.