Dạng 1: Các phép tính với số tự nhiên Toán nâng cao lớp 4
Tải vềKhi cộng một số tự nhiên với 305, do sơ suất, một học sinh đã bỏ quên chữ số 0 ... Một phép nhân có thừa số thứ hai là 36. Một học sinh khi thực hiện phép nhân đã quên lùi tích riêng thứ hai ...
|
Phương pháp giải: a) Phép cộng - Tổng của hai số lẻ hoặc hai số chẵn là một số chẵn - Tổng của một số lẻ với một số chẵn là một số lẻ b) Phép trừ - Hiệu của hai số lẻ hoặc hai số chẵn là một số chẵn - Hiệu giữa một số chẵn với một số lẻ là một số lẻ c) Phép nhân - Tích các số lẻ là một số lẻ - Một tích nếu có ít nhất một thừa số chẵn thì tích đó là một số chẵn - Tích của một số chẵn với một thừa số tận cùng bằng 5 thì tận cùng bằng 0. - Tích một số lẻ với một số tận cùng bằng 5 thì tận cùng bằng 5. - Tích các số tận cùng là 1 thì tận cùng là 1 - Tích các số tận cùng là 6 thì tận cùng là 6 d) Phép chia - Số lẻ không chia hết cho một số chẵn - Trong phép chia hết, thương của hai số lẻ là số lẻ - Trong phép chia hết, thương của một số chẵn với một số lẻ là số chẵn. |
Ví dụ 1. Khi cộng một số tự nhiên với 305, do sơ suất, một học sinh đã bỏ quên chữ số 0 của số hạng thứ hai nên nhận được kết quả bằng 380. Tìm kết quả đúng của phép tính đó?
Giải
Khi bỏ quên chữ số 0 của số hạng thứ hai thì thực chất học sinh đó đã cộng số hạng thứ nhất với 35.
Số hạng thứ nhất là:
380 – 35 = 345
Kết quả đúng của phép tính đó là:
345 + 305 = 650
Đáp số: 650
Ví dụ 2 . Khi cộng 1234 với một số có hai chữ số, do sơ suất, một học sinh đã đặt phép tính như sau:
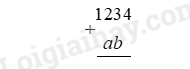
Vì vậy kết quả của phép tính tăng thêm 414 đơn vị. Tìm kết quả đúng của phép tính đó.
Giải
Theo cách đặt phép tính thì học sinh đó đã cộng số hạng thứ nhất với 10 lần số hạng thứ hai. Vậy 414 gấp số hạng thứ hai số lần là:
10 – 1 = 9 (lần)
Số hạng thứ hai trong phép cộng đó là:
414 : 9 = 46
Kết quả đúng của phép tính đó là:
1 234 + 46 = 1 280
Đáp số: 1 280
Ví dụ 3 : Tìm hai số có hiệu bằng 4441, biết rằng nếu viết thêm một chữ số 0 vào bên phải số trừ và giữ nguyên số bị trừ thì được hiệu mới là 3298.
Giải
Khi viết thêm một chữ số 0 vào bên phải số trừ thì số trừ được gấp lên 10 lần hay số trừ được thêm vào một số bằng 9 lần bản thân nó.
Khi đó hiệu mới sẽ kém hiệu ban đầu bằng 9 lần số trừ.
9 lần số trừ bằng: 4441 – 3298 = 1143
Số trừ là: 1143 : 9 = 127
Số bị trừ là: 4441 + 127 = 4568
Đáp số: 4568 ; 127
Ví dụ 4: Tìm hai số có tích bằng 5292, biết rằng nếu giữ nguyên thừa số thứ nhất và tăng thừa số thứ hai thêm 6 đơn vị thì được tích mới bằng 6048.
Giải
Khi giữ nguyên thừa số thứ nhất và tăng thừa số thứ hai thêm 6 đơn vị thì được tích mới hơn tích ban đầu một số bằng 6 lần thừa số thứ nhất.
6 lần thừa số thứ nhất bằng:
6048 – 5292 = 756
Thừa số thứ nhất bằng:
756 : 6 = 126
Thừa số thứ hai bằng:
5292 : 126 = 42
Đáp số: 126 ; 42
Ví dụ 5 . Một phép nhân có thừa số thứ hai là 36. Một học sinh khi thực hiện phép nhân đã quên lùi tích riêng thứ hai vào một số so với tích riêng thứ nhất nên dẫn đến kết quả sai là 2322. Em hãy tìm tích của phép nhân đó.
Giải
Khi đặt tích riêng thứ hai không lùi vào một cột so với tích riêng thứ nhất, ta đã lấy thừa số thứ nhất nhân với 6, sau đó nhân với 3 rồi cộng lại. Vậy kết quả so với thừa số thứ nhất thì gấp:
6 + 3 = 9 (lần)
Vậy 2322 gấp 9 lần thừa số thứ nhất.
Thừa số thứ nhất là:
2322 : 9 = 258
Tích đúng cần tìm bằng:
258 x 36 = 9 288
Đáp số: 9 288
Bài tập áp dụng:
Khi thực hiện cộng một số tự nhiên với 206, một học sinh đã chép nhầm số hạng thứ hai thành 602 nên dẫn đến kết quả sai là 1027.
a) Tìm tổng đúng của phép cộng.
b) Số hạng còn lại của phép cộng là số nào?
Khi trừ một số tự nhiên đi 208, do sơ suất, một học sinh đã bỏ quên chữ số 0 của số trừ, đồng thời viết nhầm dấu trừ thành dấu cộng nên nhận được kết quả bằng 1050. Tìm kết quả đúng của phép tính đó?
Khi nhân một số tự nhiên với 104, do sơ suất, một học sinh đã bỏ quên chữ số 0 của thừa số thứ hai nên nhận được kết quả bằng 4550. Tìm tích đúng của phép nhân đó.
