Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 3 - Hình học 9 — Không quảng cáo

Đề bài

Cho đường tròn (O) đường kính AB, Ax là tiếp tuyến của đường tròn (O) và AC là dây cung ( C khác B). Tia phân giác của $\widehat {xAC}$ cắt đường tròn (O) tại D, AD và BC cắt nhau tại E. Gọi K và F lần lượt là giao điểm của BD với AC và Ax.

a)   Chứng minh ∆ABE cân.

b)  Chứng minh tứ giác AKEF là hình thoi và EK vuông góc AB.

c)   Cho $\widehat {xAC} = 60^\circ$.

• Chứng minh DB.DK = R ² và ba điểm O, K, E thẳng hàng.
• Tính diện tích tứ giác ACEF phần nằm ngoài đường tròn.

LG ý a

Phương pháp giải:

Chứng minh BD đồng thời là đường cao của ∆ABE

Lời giải chi tiết:

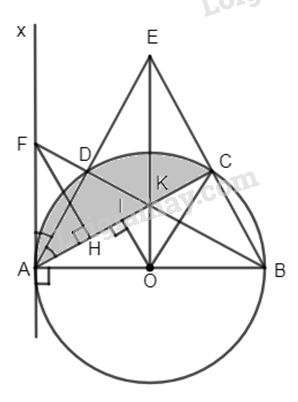
a) Ta có AD là phân giác của $\widehat {xAC}$ (gt)

$\Rightarrow \overparen{DA }= \overparen{DC}$

Do đó $\widehat {ABD} = \widehat {CBD}$ hay BD là phân giác của $\widehat {ABC}.$

Lại có BD vuông góc AD ( AB là đường kính)

∆ABE có phân giác BD đồng thời là đường cao nên ∆ABE cân tại B.

LG ý b

Phương pháp giải:

Chứng minh tứ giác EKAF là hình thoi

Sử dụng tính chất từ vuông góc đến song song

Lời giải chi tiết:

b)   Xét ∆AFK có AD là phân giác đồng thời là đường cao nên ∆AFK cân tại A. Do đó AD cũng là đường trung tuyến hay $DF = DK.$

Lại có $DA = DE$ ( ∆ABE cân).

Do đó tứ giác EKAF là hình bình hành, có hai đường chéo FK vuông góc AE nên EKAF là hình thoi.

$\Rightarrow$ EK // FA mà FA vuông góc AB (gt) $\Rightarrow$ EK vuông góc AB.

LG ý c

Phương pháp giải:

Sử dụng công thức :Diện tích hình quạt $\dfrac{{\pi {R^2}.120}}{{360}}$

${S_\text{viên phân}} = {S_q} - {S_{AOC}}$

Diện tích hình cần tính là S:

$S = {S_{ACEF}}-{S_{vp}}$

Lời giải chi tiết:

c)  Ta có : $\widehat {xAC} = 60^\circ$ (gt) $\Rightarrow \widehat {CAB} = \widehat {xAD} = \widehat {DAK} = 30^\circ$

Do đó ∆ADK và ∆BDA (gg)

$\Rightarrow \dfrac{{DA} }{ {DB}} =\dfrac {{DK}}{ {DA}} \Rightarrow D{A^2} = DB.DK$

∆ABD vuông có $\widehat {DAB} = 60^\circ$ nên $\widehat {ABD} = 30^\circ  \Rightarrow DA = R$.

Vậy DB.DK = R ² .

Dễ thấy K, E thuộc trung trực của AB nên O, K, E thẳng hàng.

● Ta có ∆ABC vuông ( AB là đường kính) có $\widehat {BAC} = 30^\circ  \Rightarrow CB = R.$

Do đó $AC = \sqrt {A{B^2} - B{C^2}}$$\,= \sqrt {{{\left( {2R} \right)}^2} - {R^2}}  = \sqrt {3{R^2}}  = R\sqrt 3$

Lại có ∆AOK và ∆ACB đồng dạng (g.g)

$\Rightarrow \dfrac{{AK} }{ {AB}} =\dfrac {{AO}}{{AC}}$

$\Rightarrow AK =\dfrac {{AB.AO} }{ {AC}} = \dfrac{{2R.R}}{ {R\sqrt 3 }} =\dfrac {{2R\sqrt 3 }}{ 3}$

Mặt khác ∆AFK đều ( cân có $\widehat {AFK} = 60^\circ$) : ${\rm{AF}} = AK = \dfrac{{2R\sqrt 3 } }{3}.$

Kẻ $FH \bot AC$ có $FH = AF.{{\sqrt 3 } \over 2} = \dfrac{{2R\sqrt 3 .\sqrt 3 } }{ 6} = R$

Dễ thấy tứ giác ACEF là hình thang ( AC // EF) nên

${S_{ACEF}} = \dfrac{{\left( {AC + {\rm{EF}}} \right).FH} }{ 2}$$\,= \dfrac{{\left( {R\sqrt 3  + {{2R\sqrt 3 } \over 3}} \right)R} }{ 2} = \dfrac{{5{R^2}\sqrt 3 } }{6}$

Ta có $\widehat {BAC} = 30^\circ$

$\Rightarrow \widehat {BOC} = 60^\circ  \Rightarrow \widehat {COA} = 120^\circ$

Khi đó hình quạt OAC có diện tích là : $\dfrac{{\pi {R^2}.120}}{{360}} =\dfrac {{\pi {R^2}} }{3}$.

Kẻ đường cao OI của tam giác AOC, ta có :

$OI = \dfrac{1}{2}OA = \dfrac{R }{2}$ ( vì ∆AOI là nửa tam giác đều)

Do đó : ${S_{AOC}} = \dfrac{1 }{ 2}AC.OI =\dfrac {1 }{ 2}R\sqrt 3 .\dfrac{R }{ 2} = \dfrac{{{R^2}\sqrt 3 } }{ 4}$

Vậy ${S_\text{viên phân}} = {S_q} - {S_{AOC}}$$\,= \dfrac{{\pi {R^2}} }{ 3} - \dfrac{{{R^2}\sqrt 3 }}{ 4} = \dfrac{{{R^2}\left( {4\pi  - 3\sqrt 3 } \right)}}{{12}}$

$\,=\dfrac{{5{R^2}\sqrt 3 } }{6} - \dfrac{{{R^2}\left( {4\pi  - 3\sqrt 3 } \right)} }{ {12}}$$\,=\dfrac {{{R^2}\left( {13\sqrt 3  - 4\pi } \right)}}{{12}}.$