Đề số 1 – Đề kiểm tra học kì 2 – Toán 9
Đáp án và lời giải chi tiết Đề số 1 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 9
Đề bài
Bài 1 (2,0 điểm):
a) Tính giá trị của biểu thức \(A = \dfrac{{\sqrt x }}{{\sqrt x + 1}}\) khi \(x = 25.\)
b) Rút gọn biểu thức \(B = \dfrac{{5\sqrt x - 9}}{{x - 5\sqrt x + 6}} + \dfrac{{\sqrt x + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x - 1}}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 4;x \ne 9.\)
c) Tìm giá trị của \(x\) thỏa mãn \(\left( {x - 9} \right).B < 2x.\)
Bài 2 (2,0 điểm): Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một xưởng theo kế hoạch phải in 6000 quyển sách giống nhau trong một thời gian quy định, với số quyển sách in được trong mỗi ngày là như nhau. Khi thực hiện mỗi ngày xưởng đã in nhiều hơn 300 quyển so với trong kế hoạch, nên xưởng đã in xong số quyển sách nói trên sớm hơn một ngày. Tính số quyển sách xưởng in được trong một ngày theo kế hoạch.
Bài 3 (2,0 điểm):
Cho phương trình: \({x^2} - 2mx + {m^2} - m + 1 = 0\)
a) Giải phương trình khi \(m = 1.\)
b) Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_2^2 + 2m{x_1} = 9.\)
Bài 4 (3,5 điểm):
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB.\) Kẻ tiếp tuyến \(Ax\) và lấy trên tiếp tuyến đó một điểm \(P\) sao cho \(AP > R,\) từ \(P\) kẻ tiếp tuyến tiếp xúc với \(\left( {O;R} \right)\) tại \(M\).
a) Chứng minh tứ giác \(APMO\) nội tiếp một đường tròn.
b) Chứng minh \(BM\,{\rm{//}}\,OP.\)
c) Đường thẳng vuông góc với \(AB\) ở \(O\) cắt tia \(BM\) tại \(N.\) Chứng minh tứ giác \(OBNP\) là hình bình hành.
d) Biết \(AN\) cắt \(OP\) tại \(K,\,\,PM\) cắt \(ON\) tại \(I;\,\,PN\) và \(OM\) kéo dài cắt nhau tại \(J.\) Chứng minh ba điểm \(I,\,\,J,\,\,K\) thẳng hàng.
Bài 5 (0,5 điểm):
Cho hai số dương \(x > 0,y > 0\) thỏa mãn \(x + y \le 1.\)
Tìm giá trị nhỏ nhất của biểu thức \(A = \dfrac{1}{{{x^2} + {y^2}}} + \dfrac{2}{{xy}} + 4xy.\)
LG bài 1
Phương pháp giải:
a) Tìm điều kiện xác định, thay giá trị của \(x = 25\,\,\left( {tm} \right)\) vào biểu thức và tính giá trị của biểu thức.
b) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức đã cho.
c) Thay biểu thức \(B\) vừa rút gọn ở câu trên vào bất phương trình, giải bất phương trình tìm \(x.\)
Đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
a) Tính giá trị của biểu thức \(A = \dfrac{{\sqrt x }}{{\sqrt x + 1}}\) khi \(x = 25.\)
Điều kiện xác định: \(x \ge 0.\)
Thay \(x = 25\,\,\,\left( {tm} \right)\) vào biểu thức ta có: \(A = \dfrac{{\sqrt {25} }}{{\sqrt {25} + 1}} = \dfrac{5}{6}.\)
Vậy \(x = 25\) thì \(A = \dfrac{5}{6}.\)
b) Rút gọn biểu thức \(B = \dfrac{{5\sqrt x - 9}}{{x - 5\sqrt x + 6}} + \dfrac{{\sqrt x + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x - 1}}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 4;x \ne 9.\)
Với \(x \ge 0;x \ne 4;x \ne 9,\) ta có:
\(\begin{array}{l}B = \dfrac{{5\sqrt x - 9}}{{x - 5\sqrt x + 6}} + \dfrac{{\sqrt x + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x - 1}}{{\sqrt x - 2}}\\B = \dfrac{{5\sqrt x - 9}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}} - \dfrac{{\sqrt x + 2}}{{\sqrt x - 3}} + \dfrac{{\sqrt x - 1}}{{\sqrt x - 2}}\\B = \dfrac{{5\sqrt x - 9 - \left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right) + \left( {\sqrt x - 1} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}\\B = \dfrac{{5\sqrt x - 9 - x + 4 + x - 4\sqrt x + 3}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}\\B = \dfrac{{\sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}\\B = \dfrac{1}{{\sqrt x - 3}}.\end{array}\)
Vậy \(B = \dfrac{1}{{\sqrt x - 3}}\) với \(x \ge 0;x \ne 4;x \ne 9.\)
c) Tìm giá trị của \(x\) thỏa mãn \(\left( {x - 9} \right).B < 2x.\)
Điều kiện: \(x \ge 0;x \ne 4;x \ne 9.\)
\(\begin{array}{l}\left( {x - 9} \right).B < 2x \Leftrightarrow \left( {x - 9} \right).\dfrac{1}{{\sqrt x - 3}} < 2x\\ \Leftrightarrow \sqrt x + 3 < 2x \Leftrightarrow 2x - \sqrt x - 3 > 0\\ \Leftrightarrow \left( {\sqrt x + 1} \right)\left( {2\sqrt x - 3} \right) > 0\\ \Leftrightarrow 2\sqrt x - 3 > 0\,\,\,\left( {do\,\,\,\sqrt x + 1 > 0} \right)\\ \Leftrightarrow \sqrt x > \dfrac{3}{2} \Leftrightarrow x > \dfrac{9}{4}.\end{array}\)
Kết hợp điều kiện, ta được \(x > \dfrac{9}{4};x \ne 4;x \ne 9\) thỏa mãn yêu cầu đề bài.
Vậy \(x > \dfrac{9}{4},\,\,x \ne 4,\,\,x \ne 9\) thỏa mãn điều kiện bài toán.
LG bài 2
Phương pháp giải:
Gọi số sách xưởng dự định in trong một ngày theo kế hoạch là \(x\) (quyển), \(\left( {x \in \mathbb{N}*,\,\,\,x < 6000} \right).\)
Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.
Lập phương trình, giải phương trình tìm \(x.\)
Đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
Gọi số sách xưởng dự định in trong một ngày theo kế hoạch là \(x\) (quyển), \(\left( {x \in \mathbb{N}*,\,\,\,x < 6000} \right).\)
\( \Rightarrow \) Số ngày hoàn thành theo dự định là: \(\dfrac{{6000}}{x}\) (ngày).
Số sách thực tế mà xưởng in được trong một ngày là: \(x + 300\) (quyển).
\( \Rightarrow \) Số ngày hoàn thành thực tế là: \(\dfrac{{6000}}{{x + 300}}\) (ngày).
Vì thực tế, xưởng in xong sớm hơn một ngày, nên ta có phương trình:
\(\begin{array}{l}\dfrac{{6000}}{x} - 1 = \dfrac{{6000}}{{x + 300}}\\ \Rightarrow 6000\left( {x + 300} \right) - x\left( {x + 300} \right) = 6000x\\ \Leftrightarrow 6000x + 1800000 - {x^2} - 300x = 6000x\\ \Leftrightarrow {x^2} + 300x - 1800000 = 0\\ \Leftrightarrow {x^2} - 1200x + 1500x - 1800000 = 0\\ \Leftrightarrow x\left( {x - 1200} \right) + 1500\left( {x - 1200} \right) = 0\\ \Leftrightarrow \left( {x - 1200} \right)\left( {x + 1500} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1200 = 0\\x + 1500 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1200\,\,\,\,\left( {tm} \right)\\x = - 1500\,\,\,\,\left( {ktm} \right)\end{array} \right..\end{array}\)
Vậy số sách xưởng dự định in trong một ngày theo kế hoạch là 1200 quyển.
LG bài 3
Phương pháp giải:
a) Thay \(m = 1\) vào phương trình, giải phương trình bậc hai một ẩn.
b) Tìm điều kiện của \(m\) để phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0.\)
Áp dụng định lý Vi-et và biểu thức đã cho để tìm \(m.\)
Đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
Cho phương trình: \({x^2} - 2mx + {m^2} - m + 1 = 0\) (*)
a) Giải phương trình khi \(m = 1.\)
Thay \(m = 1\) vào phương trình (*) đã cho, ta được phương trình:
\({x^2} - 2x + 1 = 0 \Leftrightarrow {\left( {x - 1} \right)^2} = 0\) \( \Leftrightarrow x - 1 = 0 \Leftrightarrow x = 1.\)
Vậy khi \(m = 1\) thì phương trình có nghiệm \(x = 1.\)
b) Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_2^2 + 2m{x_1} = 9.\)
Ta có: \(\Delta ' = {m^2} - \left( {{m^2} - m + 1} \right) = m - 1\)
Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\left( {ld} \right)\\m - 1 > 0\end{array} \right. \Leftrightarrow m > 1\)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = {m^2} - m + 1\end{array} \right.\)
Vì \({x_2}\) là nghiệm của phương trình (*) nên ta có:
\({x_2}^2 - 2m{x_2} + {m^2} - m + 1 = 0\)\( \Rightarrow {x_2}^2 = 2m{x_2} - {m^2} + m - 1\)
Theo đề bài ta có:
\(\begin{array}{l}x_2^2 + 2m{x_1} = 9\\ \Rightarrow \left( {2m{x_2} - {m^2} + m - 1} \right) + 2m{x_1} = 9\\ \Leftrightarrow 2m\left( {{x_1} + {x_2}} \right) - {m^2} + m - 10 = 0\\ \Leftrightarrow 2m.2m - {m^2} + m - 10 = 0\\ \Leftrightarrow 3{m^2} + m - 10 = 0\\ \Leftrightarrow 3{m^2} + 6m - 5m - 10 = 0\\ \Leftrightarrow 3m\left( {m + 2} \right) - 5\left( {m + 2} \right) = 0\\ \Leftrightarrow \left( {m + 2} \right)\left( {3m - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 2 = 0\\3m - 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 2\,\,\,\left( {ktm} \right)\\m = \dfrac{5}{3}\,\,\,\left( {tm} \right)\end{array} \right..\end{array}\)
Vậy \(m = \dfrac{5}{3}\).
LG bài 4
Phương pháp giải:
a) Chứng minh tứ giác nội tiếp dựa vào các dấu hiệu nhận biết.
b) Chứng minh hai đường thẳng cùng vuông góc với \(AM.\)
c) Chứng minh \(OP = BN,OP{\rm{ // }}BN.\)
d) Chứng minh \(I\) là trực tâm của \(\Delta OPJ\) và \(JK\) là một đường cao của\(\Delta OPJ.\)
Lời giải chi tiết:
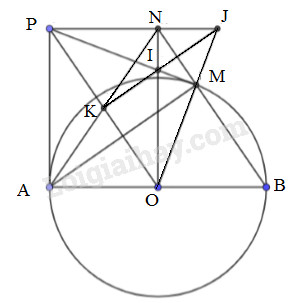
a) Chứng minh tứ giác \(APMO\) nội tiếp một đường tròn.
Ta có: \(P \in Ax\) là tiếp tuyến của \(\left( O \right) \Rightarrow AP \bot AO \Rightarrow \angle PAO = {90^0}\)
Lại có: \(PM\) cũng là tiếp tuyến của \(\left( O \right) \Rightarrow OM \bot PM \Rightarrow \angle OMP = {90^0}\)
Xét tứ giác \(APMO\) ta có: \(\angle OMP + \angle PAO\) \( = {90^0} + {90^0} = {180^0}\) mà hai góc \(\angle OMP,\angle PAO\) ở vị trí đối nhau
\( \Rightarrow APMO\) là tứ giác nội tiếp. (dhnb)
b) Chứng minh \(BM\,{\rm{//}}\,OP.\)
Xét đường tròn \((O)\) có \(PA,\,\,PM\) là hai tiếp tuyến cắt nhau tại \(P\)\( \Rightarrow PA = PM\) (tính chất)
\( \Rightarrow P\) thuộc đường trung trực của \(AM\) (1)
Lại có: \(OA = OM\,\,\left( { = R} \right) \Rightarrow O\) thuộc đường trung trực của \(AM\) (2)
Từ (1) và (2) ta có \(PO\) là đường trung trực của \(AM.\)
\( \Rightarrow PO \bot AM.\)
Lại có: \(\angle AMB\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right) \Rightarrow \angle AMB = {90^0}\) hay \(AM \bot BM.\)
\( \Rightarrow OP//BM\) (cùng \( \bot AM\)).
c) Đường thẳng vuông góc với \(AB\) ở \(O\) cắt tia \(BM\) tại \(N.\) Chứng minh tứ giác \(OBNP\) là hình bình hành.
Ta có: \(OP//BM\,\,\,\,\left( {cmt} \right)\) \( \Rightarrow \angle AOP = \angle OBN\) (hai góc đồng vị).
Xét \(\Delta APO\) và \(\Delta ONB\) ta có:
\(\begin{array}{l}\angle PAO = \angle NOB\, = {90^0}\\OA = OB = R\\\angle AOP = \angle OBN\,\,\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta PAO = \Delta NOB\,\) (cạnh huyền- góc nhọn)
\( \Rightarrow OP = NB\) (hai cạnh tương ứng bằng nhau).
Xét tứ giác \(OBNP\) ta có: \(\left\{ \begin{array}{l}OP//BN\,\,\,\left( {cmt} \right)\\OP = BN\,\,\,\,\left( {cmt} \right)\end{array} \right.\)
\( \Rightarrow OBNP\) là hình bình hành. (dhnb)
d) Biết \(AN\) cắt \(OP\) tại \(K,\,\,PM\) cắt \(ON\) tại \(I;\,\,PN\) và \(OM\) kéo dài cắt nhau tại \(J.\) Chứng minh ba điểm \(I,\,\,J,\,\,K\) thẳng hàng.
Ta có: \(\Delta APO = \Delta ONB\,\,\left( {cmt} \right)\)\( \Rightarrow AP = ON\) (hai cạnh tương ứng).
Lại có: \(\left\{ \begin{array}{l}AP \bot AB\\ON \bot AB\end{array} \right. \Rightarrow AP//ON\)
\( \Rightarrow OAPN\) là hình bình hành. (dhnb)
Mà \(\angle PAO = {90^0} \Rightarrow OAPN\) là hình chữ nhật. (dhnb)
Mặt khác: \(AN \cap OP = \left\{ K \right\}\)\( \Rightarrow K\) là trung điểm của của \(OP\) (tính chất hình bình hành)
Xét \(\left( O \right)\) ta có: \(PM\) và \(PA\) là hai tiếp tuyến cắt nhau tại \(P\)
\( \Rightarrow OP\) là tia phân giác của \(\angle AON\)
Hay \(\angle AOP = \angle POM\)
Mà \(\angle AOP = \angle NPO\) (hai góc so le trong)
\( \Rightarrow \angle MOP = \angle NPO\,\,\,\)\(hay\,\,\,\angle MOP = \angle JPO\)
\( \Rightarrow \Delta JPO\) cân tại \(J\)
Mà \(K\) là trung điểm của \(OP\,\,\left( {cmt} \right)\) nên \(JK\) vừa là đường trung tuyến trong tam giác cân \(JPO\).
Suy ra \(JK\) cũng là đường cao của \(\Delta JPO.\) (*)
Ta có: \(PM \bot OM\,\,\,hay\,\,\,PM \bot OJ\) (\(PM\) là tiếp tuyến của \(\left( O \right)\))
\( \Rightarrow PM\) là đường cao của \(\Delta OPJ.\)
Lại có: \(ON \bot PJ\) (\(OAPN\) là hình chữ nhật)
\( \Rightarrow ON\) là đường cao của \(\Delta OPJ.\)
Mà \(PM \cap ON = \left\{ I \right\}\) \( \Rightarrow I\) là trực tâm \(\Delta OPJ.\) (**)
Từ (*) và (**) \( \Rightarrow I;\,\,J;\,\,K\) thẳng hàng.
LG bài 5
Phương pháp giải:
Chọn điểm rơi và sử dụng hệ quả của bất đẳng thức AM-GM.
Lời giải chi tiết:
Cho hai số dương \(x > 0,y > 0\) thỏa mãn \(x + y \le 1.\)
Tìm giá trị nhỏ nhất của biểu thức \(A = \dfrac{1}{{{x^2} + {y^2}}} + \dfrac{2}{{xy}} + 4xy.\)
Trước tiên, theo bất đẳng thức AM-GM:
Với \(a,b > 0:\) \(\left\{ \begin{array}{l}a + b \ge 2\sqrt {ab} \\\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{2}{{\sqrt {ab} }}\end{array} \right.,\) nhân theo vế hai bất đẳng thức này ta được:
\(\left( {a + b} \right)\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right) \ge 4\) \( \Rightarrow \dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\,\,\,\,\left( * \right)\)
Ta có: \(A = \dfrac{1}{{{x^2} + {y^2}}} + \dfrac{2}{{xy}} + 4xy\)\( = \left( {\dfrac{1}{{{x^2} + {y^2}}} + \dfrac{1}{{2xy}}} \right) + \left( {\dfrac{1}{{4xy}} + 4xy} \right) + \dfrac{5}{{4xy}}.\)
Sử dụng hệ quả (*) ta có: \(\dfrac{1}{{{x^2} + {y^2}}} + \dfrac{1}{{2xy}} \ge \dfrac{4}{{{{\left( {x + y} \right)}^2}}} \ge 4\) (do \(x + y \le 1\) )
Lại có : \(\dfrac{1}{{4xy}} + 4xy\)\( \ge 2\sqrt {\dfrac{1}{{4xy}}.4xy} = 2\)
Vì \({\left( {x - y} \right)^2} \ge 0 \Rightarrow 4xy \le {\left( {x + y} \right)^2} \le 1\) \( \Rightarrow \dfrac{5}{{4xy}} \ge 5.\)
Suy ra \(A \ge 4 + 2 + 5 = 11.\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x = y\\xy = \dfrac{1}{4}\\x + y \le 1\end{array} \right.\) \( \Leftrightarrow x = y = \dfrac{1}{2}\)
Vậy giá trị nhỏ nhất của \(A\) là \(11\) khi \(x = y = \dfrac{1}{2}.\)
Nguồn: Sưu tầm