Đề thi học kì 1 Toán 10 Cánh diều - Đề số 5
Câu 1: (ID: 592114) Câu nào sau đây không phải là mệnh đề? A. Bạn bao nhiêu tuổi? B. Hôm nay là chủ nhật. C. Trái đất hình tròn. D. \(4 \ne 5\)
Đề bài
Phần 1: Trắc nghiệm (25 câu – 5 điểm)
Câu 1: (ID: 592114) Câu nào sau đây không phải là mệnh đề?
A. Bạn bao nhiêu tuổi? B. Hôm nay là chủ nhật. C. Trái đất hình tròn. D. \(4 \ne 5\)
Câu 2 : (ID: 592018) Cho hai vectơ \(\vec a\) và \(\vec b\) khác \(\vec 0\). Xác định góc \(\alpha \) giữa hai vectơ \(\vec a\) và \(\vec b\) khi \(2\vec a.\vec b{\rm{ \;}} = {\rm{ \;}} - \left| {\vec a} \right|.\left| {\vec b} \right|\).
A. \(\alpha {\rm{ \;}} = {180^0}.\) B. \(\alpha {\rm{ \;}} = {120^0}.\) C. \(\alpha {\rm{ \;}} = {90^0}.\) D. \(\alpha {\rm{ \;}} = {60^0}.\)
Câu 3: (ID: 592116) Cho tam giác ABC có M, N, Q lần lượt là trung điểm của AB, BC, CA. Khi đó vectơ \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BM} {\rm{ \;}} + \overrightarrow {NA} {\rm{ \;}} + \overrightarrow {BQ} \) bằng vectơ nào sau đây?
A. \(\overrightarrow {CB} .\) B. \(\overrightarrow {BA} .\) C. \(\vec 0.\) D. \(\overrightarrow {BC} .\)
Câu 4: (ID: 592117) Cho tam giác ABC có AB = 6, AC = 8 và \(\angle BAC = {120^0}\). Độ dài cạnh BC bằng:
A. 10. B. \(2\sqrt {13} .\) C. 12. D. \(2\sqrt {37} .\)
Câu 5: (ID: 592118) Cặp số (x;y) nào là sau đây là một nghiệm của bất phương trình x – y + 3 > 0.
A. (x;y) = (0;4). B. (x;y) = (2;5). C. (x;y) = (1;3). D. (x;y) = (1;4).
Câu 6: (ID: 592119) Cho hình bình hành ABCD. Nếu viết được \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = k\overrightarrow {AC} \) thì k bằng
A. 4. B. 3. C. 2. D. 1.
Câu 7: (ID: 592120) Gọi a, b, c, r, R, S lần lượt là độ dài ba cạnh, bán kính đường tròn nội tiếp, ngoại tiếp và diện tích của tam giác ABC. Khẳng định nào sau đây là đúng
A. \(S = p.R\) với \(p = \frac{{a + b + c}}{2}.\)
B. \(S = \frac{{abc}}{{4R}}\).
C. \(S = \frac{1}{2}\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) với \(p = \frac{{a + b + c}}{2}.\)
D. \(S = \frac{1}{2}ab\cos C\).
Câu 8: Tập xác định của hàm số \(y = \sqrt {{x^2} - 3x + 2} + \frac{1}{{\sqrt {x + 3} }}\) là
A. \(\left( { - 3; + \infty } \right)\). B. \(\left( { - 3;1} \right] \cup \left[ {2; + \infty } \right)\). C. \(\left( { - 3;1} \right] \cup \left( {2; + \infty } \right)\). D. \(\left( { - 3;1} \right) \cup \left( {2; + \infty } \right)\).
Câu 9: (ID: 590741) Cho hai tập hợp \(P = \left[ { - 4;5} \right)\) và \(Q = \left( { - 3; + \infty } \right)\). Khẳng định nào sau đây là đúng ?
A. \(P\backslash Q = \left[ { - 4; - 3} \right].\) B. \(P \cap Q = \left( { - 3;5} \right].\)
C. \(P \cup Q = \left[ { - 4;5} \right).\) D. \({C_\mathbb{R}}P = \left( { - \infty ; - 4} \right] \cup \left[ {5; + \infty } \right).\)
Câu 10: (ID: 592122) Cho các tập hợp A, B, C được minh họa bằng biểu đồ Ven như hình vẽ. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
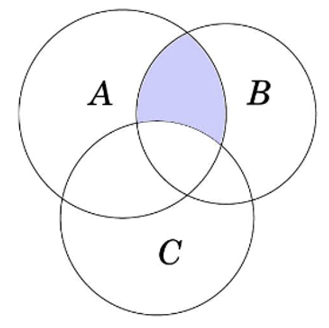
A. \(A \cap B \cap C.\) B. \(\left( {A\backslash C} \right) \cup \left( {A\backslash B} \right).\) C. \(\left( {A \cup B} \right)\backslash C.\) D. \(\left( {A \cap B} \right)\backslash C.\)
Câu 11: (ID: 592123) Khoảng cách từ điểm A đến điểm B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 52 0 16’. Biết CA = 200m, BC = 180m. Tính khoảng cách từ A đến B (làm tròn đến hàng đơn vị).

A. 165m. B. 166m. C. 169m. D. 168m.
Câu 12: (ID: 590916) Biết \(\sin x = \frac{1}{2}\). Giá trị của biểu thức \(P = {\sin ^2}x - {\cos ^2}x\) là
A. \(\frac{1}{2}\) B. \( - \frac{1}{2}\) C. \( - \frac{1}{2} + \frac{{\sqrt 3 }}{2}\) D. \( - \frac{1}{2} - \frac{{\sqrt 3 }}{2}\)
Câu 13: Cho hàm số \(f\left( x \right) = \frac{4}{{x + 1}}\). Khi đó:
A. \(f\left( x \right)\) tăng trên khoảng \(\left( { - \infty ; - 1} \right)\) và giảm trên khoảng \(\left( { - 1; + \infty } \right)\).
B. \(f\left( x \right)\) tăng trên hai khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
C. \(f\left( x \right)\) giảm trên khoảng \(\left( { - \infty ; - 1} \right)\) và giảm trên khoảng \(\left( { - 1; + \infty } \right)\).
D. \(f\left( x \right)\) giảm trên hai khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
Câu 14: (ID: 592124) Giá trị của biểu thức \(A = {\sin ^2}{51^0} + {\sin ^2}{55^0} + {\sin ^2}{39^0} + {\sin ^2}{35^0}\) là:
A. 3. B. 4. C. 1. D. 2.
Câu 15: (ID: 592125) Cho ba lực \(\overrightarrow {{F_1}} {\rm{ \;}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} {\rm{ \;}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} {\rm{ \;}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 100N và \(\angle AMB = {60^0}\). Khi đó cường độ lực \(\overrightarrow {{F_3}} \) là:
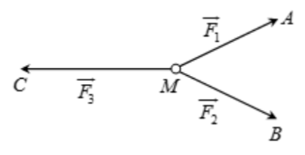
A. \(50\sqrt 2 N\). B. \(50\sqrt 3 N\). C. \(25\sqrt 3 N\). D. \(100\sqrt 3 N\).
Câu 16: Tọa độ đỉnh của parabol \(y = - 2{x^2} - 4x + 6\) là
A. \(I\left( { - 1;8} \right)\) . B. \(I\left( {1;0} \right)\) . C. \(I\left( {2; - 10} \right)\) . D. \(I\left( { - 1;6} \right)\) .
Câu 17 : (ID: 591056) Trong đợt hội diễn văn nghệ chào mừng 20/11, lớp 10A đăng kí tham gia 3 tiết mục là hát tốp ca, múa và diễn kịch. Trong danh sách đăng kí, có 7 học sinh đăng kí tiết mục hát tốp ca, 6 học sinh đăng kí tiết mục múa, 8 học sinh đăng kí diễn kịch; trong đó có 3 học sinh đăng kí cả tiết mục hát tốp ca và tiết mục múa, 4 học sinh đăng kí cả tiết mục hát tốp ca và diễn kịch, 2 học sinh đăng kí cả tiết mục múa và diễn kịch, 1 học sinh đăng kí cả 3 tiết mục. Hỏi lớp 10A có tất cả bao nhiêu học sinh đăng kí tham gia hội diễn văn nghệ?
A. 14. B. 13. C. 21. D. 11.
Câu 18 : (ID: 591999) Cho hình chữ nhật ABCD biết AB = 4a, AD = 3a. Gọi O là giao điểm của hai đường chéo AC và BD. Tính độ dài \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} \).
A. 7a. B. \(\frac{7}{2}a.\) C. \(\frac{5}{2}a.\) D. 5a.
Câu 19: Biết đồ thị hàm số \(y = a{x^2} + bx + c\), \(\left( {a,\,b,\,c\, \in \mathbb{R};\,a \ne 0} \right)\) đi qua điểm \(A\left( {2;1} \right)\) và có đỉnh \(I\left( {1\,;\, - 1} \right)\). Tính giá trị biểu thức \(T = {a^3} + {b^2} - 2c\).
A. \(T = 22\). B. \(T = 9\). C. \(T = 6\). D. \(T = 1\).
Câu 2 0 : Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình dưới
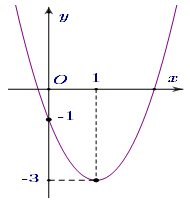
Phương trình của parabol này là
A. \(y = - {x^2} + x - 1\). B. \(y = 2{x^2} + 4x - 1\). C. \(y = {x^2} - 2x - 1\). D. \(y = 2{x^2} - 4x - 1\).
Câu 21: (ID: 590911) Đường thẳng \( - x + 3y > 2\) chia mặt phẳng tọa độ thành các miền như hình vẽ. Xác định miền nghiệm của \( - x + 3y > 2\).
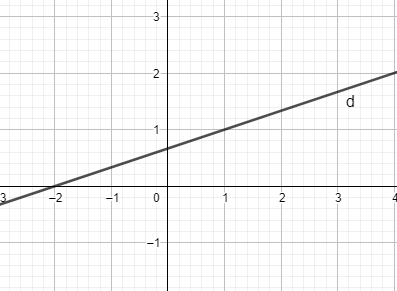
A. Nửa mặt phẳng có bờ là d cùng phía gốc tọa độ O và có lấy đường thẳng d.
B. Nửa mặt phẳng có bờ là d khác phía gốc tọa độ O và có lấy đường thẳng d.
C. Nửa mặt phẳng có bờ là d cùng phía gốc tọa độ O và không lấy đường thẳng d.
D. Nửa mặt phẳng có bờ là d khác phía gốc tọa độ O và không lấy đường thẳng d.
Câu 22: (ID: 590913) Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y > {\rm{ \;}} - 4}\\{3x - y < 5}\\{x + 1 > 0}\end{array}} \right.\).
A. \(\left( { - 2, - 3} \right)\) B. \(\left( {2, - 3} \right)\) C. \(\left( {4,0} \right)\) D. \(\left( {0,2} \right)\)
Câu 23: (ID: 590761) Cho tam giác ABC thỏa mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(\cos B + \cos C = 2\cos A.\) B. \(\sin B + \sin C = 2\sin A.\)
C. \(\sin B + \sin C = \frac{1}{2}\sin A.\) D. \(\sin B + \cos C = 2\sin A.\)
Câu 24: (ID: 591057) Cho tam giác đều ABC có độ dài các cạnh bằng 4 và điểm M thỏa mãn \(\overrightarrow {BM} {\rm{ \;}} = {\rm{ \;}} - \frac{1}{2}\overrightarrow {BC} \). Tính tích vô hướng \(\overrightarrow {BM} .\overrightarrow {BA} \).
A. \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = 4.\) B. \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} - 4\sqrt 3 .\) C. \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = 4\sqrt 3 .\) D. \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} - 4.\)
Câu 25: Cho hàm số \(y = a{x^2} + bx + c\) có bảng biến thiên dưới đây. Đáp án nào sau đây là đúng?
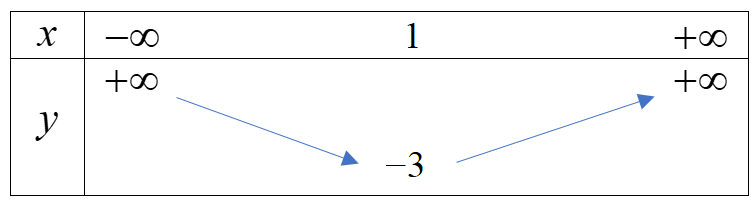
A. \(y = {x^2} + 2x - 2.\) B. \(y = {x^2} - 2x - 2.\) C. \(y = {x^2}{\rm{ + 3}}x - 2.\) D. \(y = - {x^2} - 2x - 2.\)
Phần 2: Tự luận ( 5 điểm)
Câu 1: (ID: 592127) Cho tam giác ABC. Gọi M là điểm thỏa mãn \(3\overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\) và G là trọng tâm của tam giác ABC.
a) Chứng minh rằng \(\overrightarrow {MG} {\rm{ \;}} = \frac{1}{{12}}\overrightarrow {AC} {\rm{ \;}} - \frac{5}{{12}}\overrightarrow {AB} \).
b) Gọi K là giao điểm của hai đường thẳng AC và MG. Tính tỉ số \(\frac{{KA}}{{KC}}.\)
Câu 2:
a) Xác định parabol \((P):y = a{x^2} + bx + c\), biết rằng \((P)\) có đỉnh \(I(2; - 1)\) và cắt trục tung tại điểm có tung độ bằng -3.
b) Xét sự biến thiên và vẽ đồ thị hàm số (P) tìm được.
Câu 3: (ID: 592128) Cho tam giác ABC có BC = 3 thỏa mãn \(4\sin A\tan A = \sin B\sin C\). Gọi G là trọng tâm tam giác ABC. Tính giá trị biểu thức \(S = G{B^2} + G{C^2} + 9G{A^2}\).
----- HẾT -----
Lời giải
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (25 câu – 5 điểm)
|
1.A |
2.B |
3.B |
4.D |
5.C |
6.C |
7.D |
8.B |
9.A |
10.D |
|
11.D |
12.B |
13.C |
14.D |
15.D |
16.A |
17.B |
18.C |
19.A |
2 0.D |
|
21.D |
22.D |
23.B |
24.B |
25.B |
Câu 1 (NB):
Phương pháp:
Mệnh đề là câu khẳng định có tính đúng hoặc sai.
Cách giải:
Bạn bao nhiêu tuổi? là câu nghi vấn nên không phải là mệnh đề.
Chọn A.
Câu 2 (TH):
Phương pháp:
Sử dụng định nghĩa tích vô hướng của hai vectơ: \(\vec a.\vec b{\rm{ \;}} = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\).
Cách giải:
Ta có:
\(\begin{array}{l}\vec a.\vec b = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow 2\vec a.\vec b = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow - \left| {\vec a} \right|.\left| {\vec b} \right| = 2\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\\ \Leftrightarrow \left| {\vec a} \right|.\left| {\vec b} \right|\left[ {1 + 2\cos \left( {\vec a,\vec b} \right)} \right] = 0\\ \Leftrightarrow \cos \left( {\vec a,\vec b} \right) = - \frac{1}{2}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} \vec a \ne \vec 0,{\mkern 1mu} {\mkern 1mu} \vec b \ne \vec 0} \right)\end{array}\)
\( \Leftrightarrow \left( {\vec a,\vec b} \right) = {120^0}.\)
Chọn B.
Câu 3 (TH):
Phương pháp:
Sử dụng quy tắc ba điểm.
Sử dụng hai vectơ bằng nhau.
Cách giải:
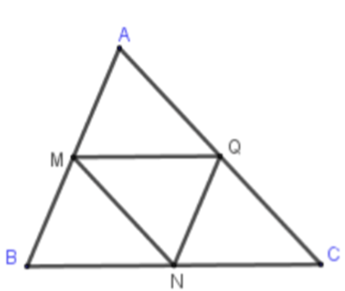
Ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BM} {\rm{ \;}} + \overrightarrow {NA} {\rm{ \;}} + \overrightarrow {BQ} }\\{ = \overrightarrow {AM} {\rm{ \;}} + \overrightarrow {NA} {\rm{ \;}} + \overrightarrow {BQ} }\\{ = \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {BQ} {\rm{ \;}} + \overrightarrow {NA} }\\{ = \overrightarrow {MQ} {\rm{ \;}} + \overrightarrow {NA} }\\{ = \overrightarrow {BN} {\rm{ \;}} + \overrightarrow {NA} }\\{ = \overrightarrow {BA} }\end{array}\)
Chọn B.
Câu 4 (NB):
Phương pháp:
Sử dụng định lí cosin trong tam giác: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \angle BAC.\)
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \angle BAC.}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {6^2} + {8^2} - 2.6.8.\cos {{120}^0}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 148}\\{ \Rightarrow BC = \sqrt {148} {\rm{ \;}} = 2\sqrt {37} .}\end{array}\)
Chọn D.
Câu 5 (NB):
Phương pháp:
Cặp số nào thỏa mãn bất phương trình là nghiệm của bất phương trình.
Cách giải:
Thay cặp số (x;y) = (0;4) vào bất phương trình: 0 – 4 + 3 > 0 => Sai.
Thay cặp số (x;y) = (2;5) vào bất phương trình: 2 – 5 + 3 > 0 => Sai.
Thay cặp số (x;y) = (1;3) vào bất phương trình: 1 – 3 + 3 > 0 => Đúng.
Thay cặp số (x;y) = (1;4) vào bất phương trình: 1 – 4 + 3 > 0 => Sai.
Chọn C.
Câu 6 (TH):
Phương pháp:
Sử dụng quy tắc hình bình hành.
Cách giải:
Theo quy tắc hình bình hành ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \overrightarrow {AC} }\\{ \Rightarrow \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} = 2\overrightarrow {AC} }\\{ \Rightarrow k = 2.}\end{array}\)
Chọn C.
Câu 7 (NB):
Phương pháp:
Sử dụng các công thức tính diện tích tam giác: \(S = \frac{{abc}}{{4R}}\), \(S = \frac{1}{2}ab\sin C\), \(S = \frac{1}{2}\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \), \(S = p.R\) với \(p = \frac{{a + b + c}}{2}.\)
Cách giải:
\(S = \frac{1}{2}ab\sin C\) nên đáp án D sai.
Chọn D.
Câu 8 (TH):
Phương pháp:
\(\sqrt {f(x)} \) xác định khi \(f(x) \ge 0\)
\(\frac{1}{{g(x)}}\) xác định khi \(g(x) \ne 0\)
Cách giải:
Điều kiện: \(\left\{ \begin{array}{l}{x^2} - 3x + 2 \ge 0\\x + 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \in \left( { - \infty ;1} \right] \cup \left[ {2; + \infty } \right)\\x > - 3\end{array} \right. \Leftrightarrow x \in \left( { - 3;1} \right] \cup \left[ {2; + \infty } \right)\).
Chọn B.
Câu 9 (TH):
Phương pháp:
Biểu diễn các tập hợp trên trục số và thực hiện các phép toán trên tập hợp.
Cách giải:

\(P\backslash Q = \left[ { - 4; - 3} \right] \Rightarrow A\) đúng.
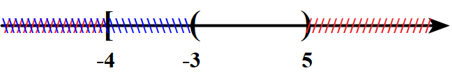
\(P \cap Q = \left( { - 3;5} \right) \Rightarrow B\) sai.
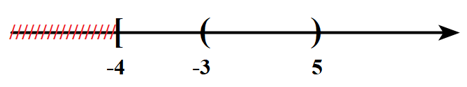
\(P \cup Q = \left[ { - 4; + \infty } \right) \Rightarrow C\) sai.
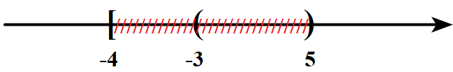
\({C_\mathbb{R}}P = \mathbb{R}\backslash P = \left( { - \infty ; - 4} \right) \cup \left[ {5; + \infty } \right) \Rightarrow D\) sai.
Chọn A.
Câu 10 (TH):
Phương pháp:
Sử dụng khái niệm các phép toán trên tập hợp.
Cách giải:
Phần tô đậm trong hình vẽ biểu diễn cho tập hợp \(\left( {A \cap B} \right)\backslash C.\)
Chọn D.
Câu 11 (TH):
Phương pháp:
Sử dụng định lí Cosin trong tam giác ABC ta có: \(A{B^2} = A{C^2} + B{C^2} - 2AC.BC.\cos C.\)
Cách giải:
Áp dụng định lí Cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{A{B^2} = A{C^2} + B{C^2} - 2AC.BC.\cos C}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {{200}^2} + {{180}^2} - 2.200.180.\cos {{52}^0}16' \approx 28337}\\{ \Rightarrow AB \approx 168{\mkern 1mu} {\mkern 1mu} \left( m \right)}\end{array}\)
Chọn D.
Câu 12 (TH):
Phương pháp:
Dùng công thức \({\sin ^2}x + {\cos ^2}x = 1\) để tính cos x
Cách giải:
\(\begin{array}{*{20}{l}}{\sin x = \frac{1}{2} \Rightarrow \sin {x^2} = \frac{1}{4} \Rightarrow {{\cos }^2}x = 1 - {{\sin }^2}x = 1 - \frac{1}{4} = \frac{3}{4}}\\{ \Rightarrow {{\sin }^2}x - {{\cos }^2}x = \frac{1}{4} - \frac{3}{4} = \frac{{ - 1}}{2}}\end{array}\)
Chọn B.
Câu 13 (VD):
Cách giải:
TXĐ: \(D = \mathbb{R}{\rm{\backslash \{ }} - 1\} \).
Xét \({x_1};\,{x_2}\, \in \,D\)và\({x_1} < {x_2} \Leftrightarrow {x_1} - {x_2} < 0\)
Khi đó với hàm số \(y = f\left( x \right) = \frac{4}{{x + 1}}\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{4}{{{x_1} + 1}} - \frac{4}{{{x_2} + 1}} = 4.\frac{{\left( {{x_2} - {x_1}} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}\)
Trên \(\left( { - \infty ; - 1} \right)\)\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = 4.\frac{{\left( {{x_2} - {x_1}} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}} > 0\)nên hàm số nghịch biến.
Trên \(\left( { - 1; + \infty } \right)\)\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = 4.\frac{{\left( {{x_2} - {x_1}} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}} > 0\)nên hàm số nghịch biến.
Vậy \(y = \left| {x + 1} \right| - \left| {1 - x} \right|\)không là hàm số chẵn.
Chọn C.
Câu 14 (TH):
Phương pháp:
Nếu \(\alpha {\rm{ \;}} + \beta {\rm{ \;}} = {90^0}\) thì \(\sin \alpha {\rm{ \;}} = \cos \beta \).
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{A = {{\sin }^2}{{51}^0} + {{\sin }^2}{{55}^0} + {{\sin }^2}{{39}^0} + {{\sin }^2}{{35}^0}}\\{A = \left( {{{\sin }^2}51 + {{\sin }^2}{{39}^0}} \right) + \left( {{{\sin }^2}{{55}^0} + {{\sin }^2}{{35}^0}} \right)}\\{A = \left( {{{\sin }^2}51 + {{\sin }^2}\left( {{{90}^0} - {{51}^0}} \right)} \right) + \left( {{{\sin }^2}{{55}^0} + {{\sin }^2}\left( {{{90}^0} - {{55}^0}} \right)} \right)}\\{A = \left( {{{\sin }^2}51 + {{\cos }^2}{{51}^0}} \right) + \left( {{{\sin }^2}{{55}^0} + {{\cos }^2}{{55}^0}} \right)}\\{A = 1 + 1 = 2.}\end{array}\)
Chọn D.
Câu 15 (TH):
Phương pháp:
Vì M đứng yên nên \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow \overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\).
Sử dụng quy tắc hình bình hành.
Cách giải:
Vì M đứng yên nên \(\overrightarrow {{F_1}} {\rm{ \;}} + \overrightarrow {{F_2}} {\rm{ \;}} + \overrightarrow {{F_3}} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow \overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0\).
Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} = \overrightarrow {MD} \), với D là đỉnh thứ tư của hình bình hành AMBD như hình vẽ.
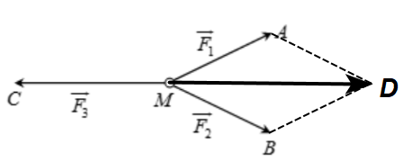
\(\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {MD} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow \overrightarrow {MC} {\rm{ \;}} = {\rm{ \;}} - \overrightarrow {MD} }\\{ \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = \left| { - \overrightarrow {MD} } \right| = MD}\end{array}\)
Vì MA = MB = 100, \(\angle AMB = {60^0}\) nên tam giác AMB đều \( \Rightarrow MD = 100\sqrt 3 \).
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = 100\sqrt 3 N.\)
Chọn D.
Câu 16 (TH):
Phương pháp:
Tọa độ đỉnh của parabol \(y = a{x^2} + bx + c\) là \(I\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
Cách giải:
Tọa độ đỉnh của parabol \(y = - 2{x^2} - 4x + 6\) là \(\left\{ \begin{array}{l}x = - \frac{{ - 4}}{{2.\left( { - 2} \right)}} = - 1\\y = - 2.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right) + 6 = 8\end{array} \right. \Rightarrow I\left( { - 1;8} \right)\).
Chọn A.
Câu 17 (VD):
Phương pháp:
Sử dụng công thức \(n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)\).
Cách giải:
Gọi A là tập hợp các bạn đăng kí tiết mục tốp ca \( \Rightarrow n\left( A \right) = 7.\)
B là tập hợp các bạn đăng kí tiết mục múa \( \Rightarrow n\left( B \right) = 6.\)
C là tập hợp các bạn đăng kí tiết mục diễn kịch \( \Rightarrow n\left( C \right) = 8.\)
\( \Rightarrow A \cap B:\) tập hợp các bạn đăng kí cả 2 tiết mục tốp ca và múa \( \Rightarrow n\left( {A \cap B} \right) = 3.\)
\(A \cap C\): tập hợp các bạn đăng kí cả 2 tiết mục tốp ca và diễn kịch \( \Rightarrow n\left( {A \cap C} \right) = 4.\)
\(B \cap C\): tập hợp các bạn đăng kí cả 2 tiết mục múa và diễn kịch \( \Rightarrow n\left( {B \cap C} \right) = 2.\)
\(A \cap B \cap C\): tập hợp các bạn đăng kí cả 3 tiết mục tốp ca, múa và diễn kịch \( \Rightarrow n\left( {A \cap B \cap C} \right) = 1.\)
\(A \cup B \cup C\): tập hợp các bạn đăng kí ít nhất 1 tiết mục.
Ta có: \(n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {C \cap A} \right) + n\left( {A \cap B \cap C} \right)\)
\( \Rightarrow n\left( {A \cup B \cup C} \right) = 7 + 6 + 8 - 3 - 4 - 2 + 1 = 13.\)
Chọn B.
Câu 18 (TH):
Phương pháp:
Sử dụng hai vectơ bằng nhau, đưa về hai vectơ chung điểm đầu và cuối, sử dụng quy tắc ba điểm.
Cách giải:
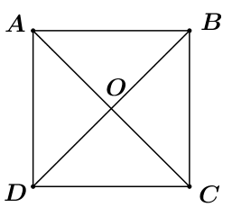
Ta có: \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} {\rm{ \;}} = \overrightarrow {OD} {\rm{ \;}} + \overrightarrow {AB} {\rm{ \;}} = \overrightarrow {OD} {\rm{ \;}} + \overrightarrow {DC} {\rm{ \;}} = \overrightarrow {OC} \).
\( \Rightarrow \left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} } \right| = \left| {\overrightarrow {OC} } \right| = OC\).
Áp dụng định lí Pytago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} {\rm{ \;}} = \sqrt {{{\left( {4a} \right)}^2} + {{\left( {3a} \right)}^2}} {\rm{ \;}} = 5a \Rightarrow OC = \frac{1}{2}AC = \frac{5}{2}a.\)
Vậy \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {OD} } \right| = OC = \frac{5}{2}a.\)
Chọn C.
Câu 19 (TH):
Phương pháp:
Tọa độ đỉnh của parabol \(y = a{x^2} + bx + c\) là \(I\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
Cách giải:
Đồ thị hàm số \(y = {\rm{a}}{{\rm{x}}^2} + bx + c\) đi qua điểm \(A\left( {2;1} \right)\) và có đỉnh \(I\left( {1\,;\, - 1} \right)\) nên có hệ phương trình
\(\left\{ \begin{array}{l}4a + 2b + c = 1\\ - \frac{b}{{2a}} = 1\\a + b + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\b = - 2a\\a + b + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\b = - 2a\\ - a + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\b = - 4\\a = 2\end{array} \right.\).
Vậy \(T = {a^3} + {b^2} - 2c = 22\).
Chọn A.
Câu 2 0 (TH):
Phương pháp:
Tọa độ đỉnh của parabol \(y = a{x^2} + bx + c\) là \(I\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
Cách giải:
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, - 1} \right)\) nên \(c = - 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, - 3} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 1\\a{.1^2} + b.1 - 1 = - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 4\end{array} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} - 4x - 1\).
Chọn D.
Câu 21 (NB):
Phương pháp:
Chọn điểm bất kì thỏa mãn bất phương trình để chọn miền nghiệm
Cách giải:
Vì O(0,0) không thuộc miền nghiệm nên nửa mặt phẳng có bờ là d khác phía gốc tọa độ O và không lấy đường thẳng d
Chọn D.
Câu 22 (NB):
Phương pháp:
Vẽ đồ thị hoặc thử các đáp án
Cách giải:
\(\left( {0,2} \right)\) thỏa mãn 3 phương trình trong hệ phương trình nên chọn D
Chọn D.
Câu 23 (TH):
Phương pháp:
Sử dụng định lí Sin trong tam giác \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Cách giải:
Sử dụng định lí Sin trong tam giác \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\) \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2R\sin A}\\{b = 2R\sin B}\\{c = 2R\sin C}\end{array}} \right.\).
Theo giả thiết ta có:
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} b + c = 2a}\\{ \Leftrightarrow 2R\sin B + 2R\sin C = 2.2R\sin A}\\{ \Leftrightarrow \sin B + \sin C = 2\sin A.}\end{array}\)
Chọn B.
Câu 24 (TH):
Phương pháp:
Sử dụng công thức \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = BM.BA.\cos \left( {\overrightarrow {BM} ,\overrightarrow {BA} } \right).\)
Cách giải:
Ta có: \(\overrightarrow {BM} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} - \frac{1}{2}\overrightarrow {BC} .\overrightarrow {BA} {\rm{ \;}} = {\rm{ \;}} - \frac{1}{2}BC.BA.\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right).\)
Vì tam giác ABC đều nên \(\cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \angle ABC = {60^0}\).
\( \Rightarrow \overrightarrow {BM} .\overrightarrow {BA} = - \frac{1}{2}.4.4.\frac{{\sqrt 3 }}{2} = {\rm{ \;}} - 4\sqrt 3 .\)
Chọn B.
Câu 25 (TH):
Phương pháp:
Tọa độ đỉnh của parabol \(y = a{x^2} + bx + c\) là \(I\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
Cách giải:
Từ BBT ta có \(a > 0\) nên loại đáp án D. Đỉnh \(I\left( {1; - 3} \right)\) nên \( - \frac{b}{{2{\rm{a}}}} = 1\)
Đáp án A. \(y = {x^2} + 2x - 2\) có \(a = 1,b = 2 \Rightarrow \frac{{ - b}}{{2a}} = - 1\) (Loại)
Đáp án B. \(y = {x^2} - 2x - 2\) có \(a = 1,b = - 2 \Rightarrow \frac{{ - b}}{{2a}} = 1\) (TM)
Đáp án C. \(y = {x^2} + 3x - 2\) có \(a = 1,b = 3 \Rightarrow \frac{{ - b}}{{2a}} = - \frac{3}{2}\) (Loại)
Chọn B.
Phần 2: Tự luận ( 5 điểm)
Câu 1 (VD):
Phương pháp:
a) Gọi I là trung điểm của BC. Chứng minh M là trung điểm của BI.
Sử dụng quy tắc ba điểm, công thức trung điểm.
b) Sử dụng điều kiện để hai vectơ cùng phương.
Cách giải:
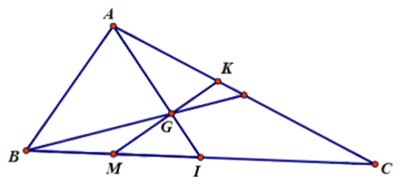
a) Gọi I là trung điểm của BC.
Ta có: \(3\overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0{\rm{ \;}} \Rightarrow 3MB = MC \Rightarrow MB = \frac{1}{4}BC = \frac{1}{2}BI\).
=> M là trung điểm của BI.
Khi đó ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {MG} = \overrightarrow {MI} + \overrightarrow {IG} = \frac{1}{4}\overrightarrow {BC} - \frac{1}{3}\overrightarrow {AI} }\\{ = \frac{1}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) - \frac{1}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)}\\{ = \frac{1}{4}\overrightarrow {AC} - \frac{1}{4}\overrightarrow {AB} - \frac{1}{6}\overrightarrow {AB} - \frac{1}{6}\overrightarrow {AC} }\\{ = \frac{1}{{12}}\overrightarrow {AC} - \frac{5}{{12}}\overrightarrow {AB} {\mkern 1mu} {\mkern 1mu} \left( {dpcm} \right).}\end{array}\)
b) Đặt \(\overrightarrow {AK} {\rm{ \;}} = x\overrightarrow {AC} {\mkern 1mu} {\mkern 1mu} \left( {x > 0} \right)\), ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {GK} {\rm{ \;}} = \overrightarrow {AK} {\rm{ \;}} - \overrightarrow {AG} {\rm{ \;}} = x\overrightarrow {AC} {\rm{ \;}} - \frac{2}{3}\overrightarrow {AI} }\\{ = x\overrightarrow {AC} {\rm{ \;}} - \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right) = \left( {x - \frac{1}{3}} \right)\overrightarrow {AC} {\rm{ \;}} - \frac{1}{3}\overrightarrow {AB} }\end{array}\)
Vì M, G, K thẳng hàng nên \(\frac{{x - \frac{1}{3}}}{{\frac{1}{{12}}}} = \frac{{ - \frac{1}{3}}}{{ - \frac{5}{{12}}}} \Leftrightarrow x = \frac{2}{5}.\)
Vậy \(\overrightarrow {AK} {\rm{\;}} = \frac{2}{5}\overrightarrow {AC} \) nên \(AK = \frac{2}{5}AC \Rightarrow \frac{{KA}}{{KC}} = \frac{2}{3}.\)
Câu 2 (VD):
Phương pháp:
a) Hàm số \(y = a{x^2} + bx + c(a \ne 0)\) có đỉnh \(\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\).
b) Sự biến thiên
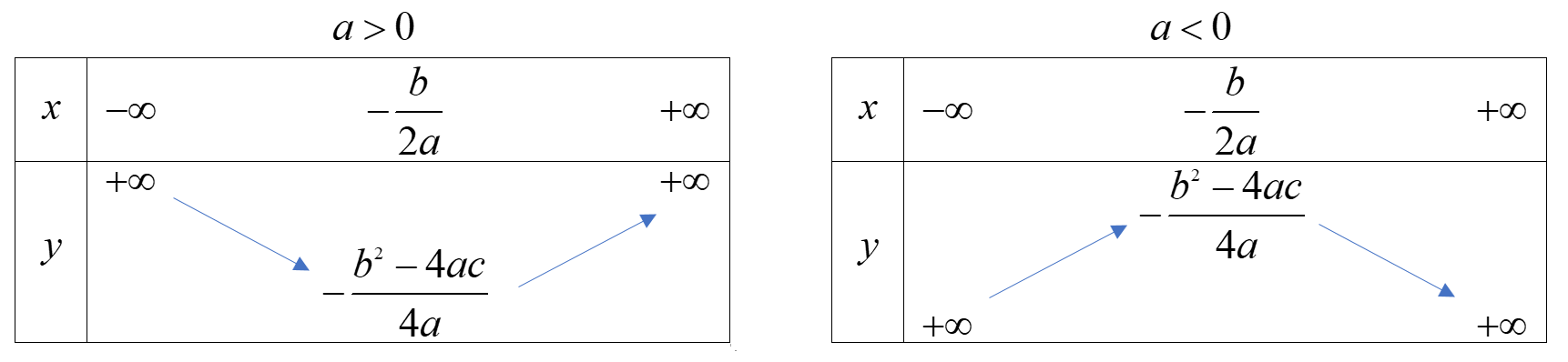
* Vẽ đồ thị
+ Đỉnh I\(\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
+ Trục đối xứng \(x = - \frac{b}{{2a}}\)
+ Giao với các trục (nếu có)
+ Lấy các điểm thuộc đồ thị (đối xứng nhau qua trục đối xứng).
Cách giải:
a) Ta có: (P) giao với Oy tại điểm có tung độ bằng -3 hay điểm (0;-3). Suy ra \(a.0 + b.0 + c = - 3 \Leftrightarrow c = - 3\)
Vì (P) có đỉnh I(2;-1) nên \(\left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = 2\\a{.2^2} + b.2 + ( - 3) = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - b = 4a\\4a + 2b - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{2}\\b = 2\end{array} \right.\)
Vậy parabol (P) là \(y = - \frac{1}{2}{x^2} + 2x - 3\)
b) Hàm số \(y = - \frac{1}{2}{x^2} + 2x - 3\) có \(a = - \frac{1}{2} < 0\), đỉnh I(2;-1) nên có bảng biến thiên:
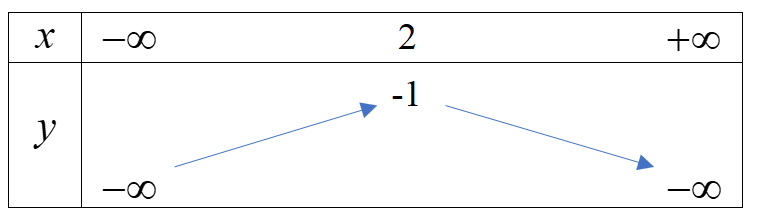
Hàm số đồng biến trên \(( - \infty ;2)\) và nghịch biến trên khoảng \((2; + \infty )\)
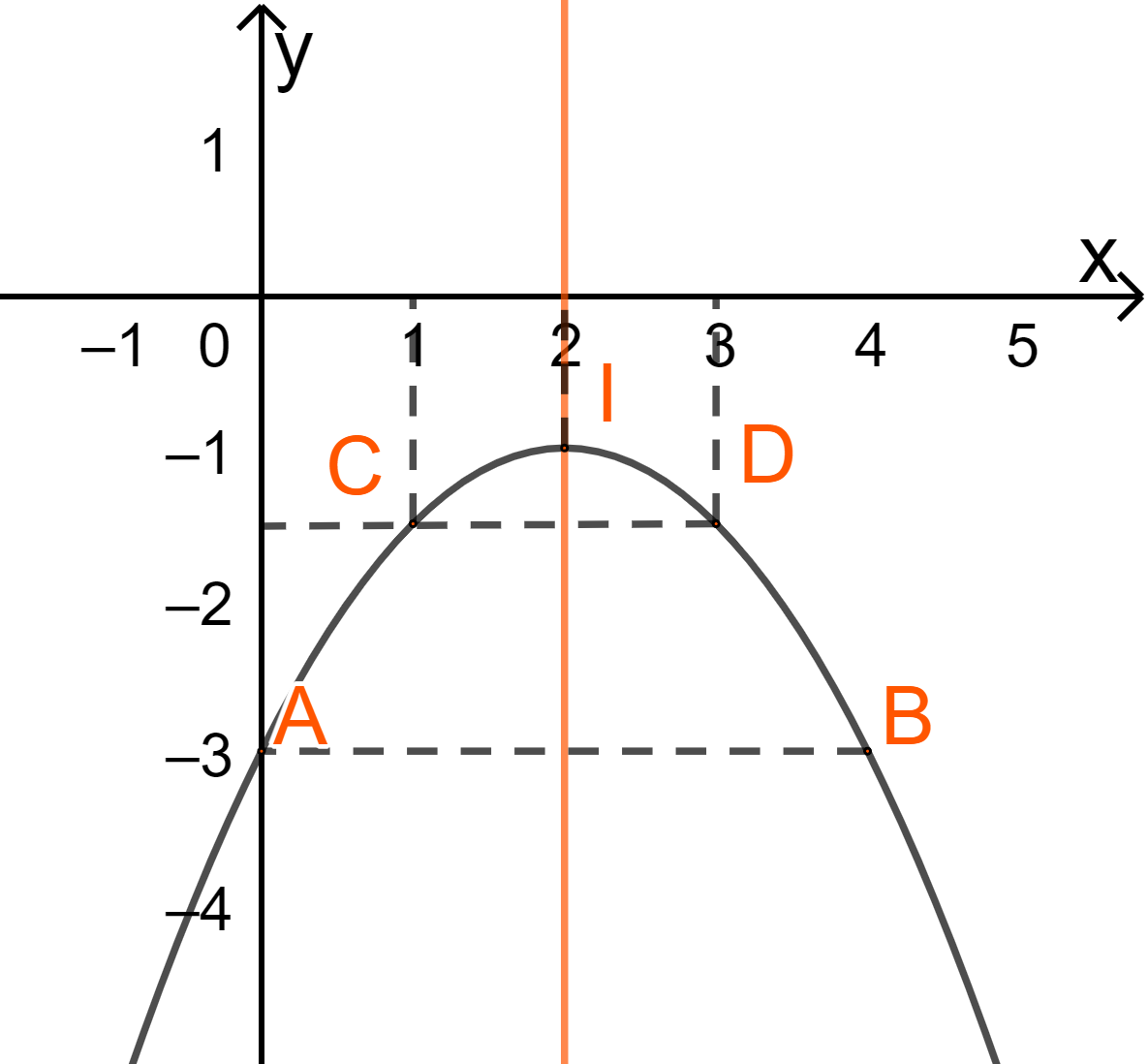
* Vẽ đồ thị
Đỉnh I(2;-1)
Trục đối xứng \(x = 2\)
Cắt trục tung tại A(0;-3) và không cắt Ox
Lấy B(4;-3) thuộc (P), đối xứng với A(0;-3) qua trục đối xứng
Lấy \(C\left( {1; - \frac{3}{2}} \right),D\left( {3; - \frac{3}{2}} \right)\) thuộc (P).
Câu 3 (VDC):
Phương pháp:
Ta thường dùng các chữ cái in hoa để kí hiệu tập hợp và chữ cái in thường để kí hiệu phần tử thuộc tập hợp.
Cách giải:
Ta có
\(\begin{array}{l}S = G{B^2} + G{C^2} + 9G{A^2}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\left( {\frac{2}{3}{m_b}} \right)^2} + {\left( {\frac{2}{3}{m_c}} \right)^2} + 9.{\left( {\frac{2}{3}{m_a}} \right)^2}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{4}{9}{m_b}^2 + \frac{4}{9}{m_c}^2 + 4{m_a}^2\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{4}{9}.\left( {\frac{{2{a^2} + 2{c^2} - {b^2}}}{4} + \frac{{2{a^2} + 2{b^2} - {c^2}}}{4}} \right) + 4.\frac{{2{b^2} + 2{c^2} - {a^2}}}{4}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{4}{9}.\frac{{4{a^2} + {b^2} + {c^2}}}{4} + 2{b^2} + 2{c^2} - {a^2}\end{array}\)
\(\begin{array}{l}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{{4{a^2} + {b^2} + {c^2}}}{9} + 2{b^2} + 2{c^2} - {a^2}\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{{19}}{9}\left( {{b^2} + {c^2}} \right) - \frac{5}{9}{a^2}\end{array}\)
Theo giả thiết ta có: \(4\sin A\tan A = \sin B\sin C \Leftrightarrow 4{\sin ^2}A = \sin B\sin C\cos A{\mkern 1mu} {\mkern 1mu} \left( * \right)\)
Áp dụng định lí sin trong tam giác ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\sin A = \frac{a}{{2R}}}\\{\sin B = \frac{b}{{2R}}}\\{\sin C = \frac{c}{{2R}}}\end{array}} \right.\)
Thay vào (*) ta có:
\(\begin{array}{*{20}{l}}{\left( * \right) \Leftrightarrow 4{{\left( {\frac{a}{{2R}}} \right)}^2} = \frac{b}{{2R}}.\frac{c}{{2R}}\cos A}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Leftrightarrow 4.\frac{{{a^2}}}{{4{R^2}}} = \frac{{bc}}{{4{R^2}}}\cos A}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Leftrightarrow 4{a^2} = bc\cos A}\end{array}\)
Lại theo định lí cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} - 2bc\cos A}\\{ \Rightarrow bc\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{2}}\end{array}\)
Khi đó ta có:
\(\begin{array}{*{20}{l}}{\left( * \right) \Leftrightarrow 4{a^2} = \frac{{{b^2} + {c^2} - {a^2}}}{2}}\\{ \Leftrightarrow 8{a^2} = {b^2} + {c^2} - {a^2}}\\{ \Leftrightarrow 9{a^2} = {b^2} + {c^2}}\end{array}\)
Do đó: \(S = \frac{{19}}{9}\left( {{b^2} + {c^2}} \right) - \frac{5}{9}{a^2} = \frac{{19}}{9}.9{a^2} - \frac{5}{9}{a^2} = \frac{{166{a^2}}}{9} = 166.\)
Vậy S = 166.