Đề thi học kì 1 Toán 10 Cánh diều - Đề số 9
Câu 1: Tìm tập xác định ({rm{D}}) của hàm số (y = sqrt {6 - 3x} + frac{1}{{sqrt {x - 1} }}.) A. ({rm{D}} = left[ {1;2} right].) B. ({rm{D}} = left( {1;2} right).) C. ({rm{D}} = (1;2].) D. ({rm{D}} = left[ { - 1;2} right].)
Đề bài
I. Trắc nghiệm ( 6 điểm)
Câu 1: Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \sqrt {6 - 3x} + \frac{1}{{\sqrt {x - 1} }}.\)
A. \({\rm{D}} = \left[ {1;2} \right].\) B. \({\rm{D}} = \left( {1;2} \right).\) C. \({\rm{D}} = (1;2].\) D. \({\rm{D}} = \left[ { - 1;2} \right].\)
Câu 2: Cho mệnh đề P(x): “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)”. Mệnh đề phủ định của mệnh đề P(x) là
A. “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 < 0\)”. B. “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”.
C. “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”. D. “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)”.
Câu 3: Cho hàm số \(.y = \frac{{\sqrt {x - 2} - 2}}{{x - 6}}\). Điểm nào sau đây thuộc đồ thị hàm số:
A. \((6;0)\). B. \((2; - 0,5)\). C. \((2;0,5)\). D. \((0;6)\).
Câu 4: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng:
A. \(A = \left\{ {x \in \mathbb{R}|\left| x \right| < 1} \right\}\) B. \(A = \left\{ {x \in \mathbb{Z}|6{x^2} - 7x + 1 = 0} \right\}\) C. \(A = \left\{ {x \in \mathbb{Z}|{x^2} - 4x + 2 = 0} \right\}\) D. \(A = \left\{ {x \in \mathbb{N}|{x^2} - 4x + 3 = 0} \right\}\)
Câu 5: Cho hai tập hợp \(A = \left( { - \infty ;2} \right]\) và \(B = \left( { - 3;5} \right]\). Tìm mệnh đề sai.
A. \(A \cap B = \left( { - 3;2} \right].\) B. \(A\backslash B = \left( { - \infty ; - 3} \right)\). C. \(A \cup B = \left( { - \infty ;5} \right]\). D. \(B\backslash A = \left( {2;5} \right]\).
Câu 6: Cho tập hợp: \(B = \left\{ {x;{\mkern 1mu} {\mkern 1mu} y;{\mkern 1mu} {\mkern 1mu} z;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 5} \right\}.\) Số tập hợp con của tập hợp \(B\) là
A. 29 B. 30 C. 31 D. 32
Câu 7: Hàm số \(y = a{x^2} + bx + c\), \((a > 0)\) nghịch biến trong khoảng nào sau đậy?
A. \(\left( { - \infty ;\, - \frac{b}{{2a}}} \right).\) B. \(\left( { - \frac{b}{{2a}};\, + \infty } \right).\) C. \(\left( { - \frac{\Delta }{{4a}};\, + \infty } \right).\) D. \(\left( { - \infty ;\, - \frac{\Delta }{{4a}}} \right).\)
Câu 8: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. \(2{x^2} + 3y > 0\) B. \({x^2} + {y^2} < 2\) C. \(x + {y^2} \ge 0\) D. \(x + y \ge 0\)
Câu 9: Miền nghiệm của bất phương trình \(\left( {1 + \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y \ge 2\) chứa điểm nào sau đây?
A. A(1;-1) B. B(-1;-1) C. C(-1;1) D. \(D\left( { - \sqrt 3 ;\sqrt 3 } \right)\)
Câu 10: (ID: 590544) Trong tam giác EFG, chọn mệnh đề đúng.
A. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos G.\) B. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos E.\)
C. \(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos E.\) D. \(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos G.\)
Câu 11: Cho hình chữ nhật ABCD có \(AB = a\) và \(AD = a\sqrt 2 \). Gọi K là trung điểm của cạnh AD. Tính \(\overrightarrow {BK} .\overrightarrow {AC} \)
A. \(\overrightarrow {BK} .\overrightarrow {AC} = \overrightarrow 0 \) B. \(\overrightarrow {BK} .\overrightarrow {AC} = - {a^2}\sqrt 2 \) C. \(\overrightarrow {BK} .\overrightarrow {AC} = {a^2}\sqrt 2 \) D. \(\overrightarrow {BK} .\overrightarrow {AC} = 2{a^2}\)
Câu 12: (ID: 590546) Cho tam giác ABC có b = 7, c = 5, \(\cos A = \frac{3}{5}.\) Độ dài đường cao \({h_a}\) của tam giác ABC là:
A. \(8.\) B. \(8\sqrt 3 .\) C. \(\frac{{7\sqrt 2 }}{2}.\) D. \(7\sqrt 2 .\)
Câu 13: Hàm số bậc hai nào sau đây có đồ thị là parabol có đỉnh là \(S\left( {\frac{5}{2};\frac{1}{2}} \right)\)và đi qua \(A\left( {1; - 4} \right)\)?
A. \(y = - {x^2} + 5x - 8\). B. \(y = - 2{x^2} + 10x - 12\) .
C. \(y = {x^2} - 5x\). D. \(y = - 2{x^2} + 5x + \frac{1}{2}\) .
Câu 14: Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
A. \(O\left( {0;0} \right)\) B. \(M\left( {1;0} \right)\) C. \(N\left( {0; - 2} \right)\) D. \(P\left( {0;2} \right)\)
Câu 15: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau

Phương trình của parabol này là
A. \(y = - {x^2} + x - 1\). B. \(y = 2{x^2} + 4x + 1\). C. \(y = {x^2} - 2x - 1\). D. \(y = 2{x^2} - 4x - 1\) .
Câu 16: Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a.
A. \(r = \frac{{a\sqrt 3 }}{4}\) B. \(r = \frac{{a\sqrt 2 }}{5}\) C. \(r = \frac{{a\sqrt 3 }}{6}\) D. \(r = \frac{{a\sqrt 5 }}{7}\)
Câu 17: Tam giác ABC có \(AB = \sqrt 2 ,\,\,AC = \sqrt 3 \) và \(C = {45^0}\). Tính độ dài cạnh BC.
A. \(BC = \sqrt 5 \) B. \(BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}\) C. \(BC = \frac{{\sqrt 6 - \sqrt 2 }}{2}\) D. \(BC = \sqrt 6 \)
Câu 18: Bảng biến thiên của hàm số \(y = - {x^2} + 2x - 1\) là:
A.
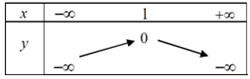 B.
B.
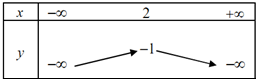
C.
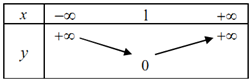 D.
D.
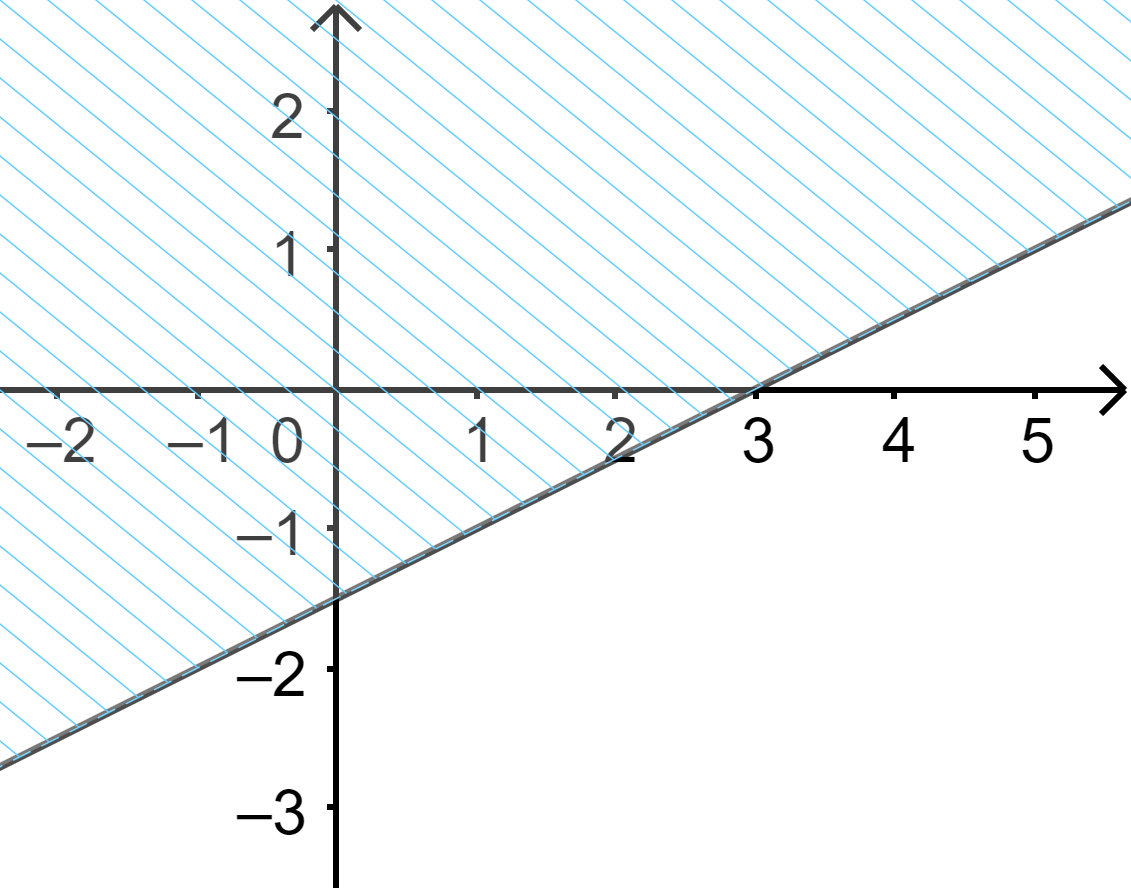
Câu 19: Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào?

A. \(\left( { - 3; + \infty } \right).\) B. \(\left( {5; + \infty } \right).\) C. \(\{ - 3;5\} \) D. \(\left( { - 3;5} \right].\)
Câu 20: Giá trị lớn nhất của hàm số \(y = - 3{x^2} + 2x + 1\) trên đoạn \(\left[ {1;3} \right]\) là:
A. \(\frac{4}{5}\) B. 0 C. \(\frac{1}{3}\) D. \( - 20\)
Câu 21: Cho hai vectơ \(\vec a\) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 3,\) \(\left| {\overrightarrow b } \right| = 2\) và \(\vec a.\vec b = - 3.\) Xác định góc \(\alpha \) giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b .\)
A. \(\alpha = {30^0}.\) B. \(\alpha = {45^0}.\) C. \(\alpha = {60^0}.\) D. \(\alpha = {120^0}.\)
Câu 22: Cho tam giác cân \(ABC\) có\(\widehat A = {120^0}\)và \(AB = AC = a\). Lấy điểm \(M\)trên cạnh \(BC\) sao cho \(BM = \frac{{2BC}}{5}\). Tính độ dài \(AM.\)
A. \(\frac{{a\sqrt 3 }}{3}\) B. \(\frac{{11a}}{5}\) C. \(\frac{{a\sqrt 7 }}{5}\) D. \(\frac{{a\sqrt 6 }}{4}\)
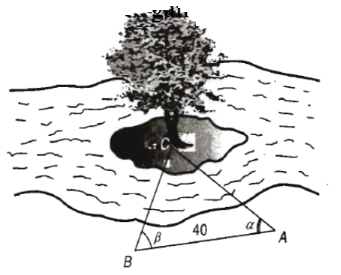
Câu 23: Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?
A. \(2x - y < 3\) B. \(2x - y > 3\) C. \(x - 2y < 3\) D. \(x - 2y > 3\)
Câu 24: Cho góc \(\alpha \) với \({0^0} < \alpha < {180^0}\). Tính giá trị của \(\cos \alpha \), biết \(\tan \alpha = - 2\sqrt 2 \).
A. \( - \frac{1}{3}.\) B. \(\frac{1}{3}.\) C. \(\frac{{2\sqrt 2 }}{3}.\) D. \(\frac{{\sqrt 2 }}{3}.\)
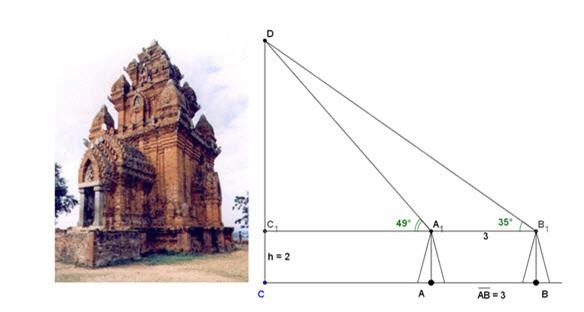
Câu 25: Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn cùng một điểm trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách AB = 40cm, \(\angle CAB = {45^0}\), \(\angle CBA = {70^0}\). Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây?
A. 53 m B. 30 m C. 41,5 m D. 41 m
Câu 26: Cho hình vuông ABCD cạnh \(a\), \(M\) là điểm thay đổi. Độ dài véctơ \(\vec u = \overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {MC} {\rm{\;}} - 3\overrightarrow {MD} \) là:
A. \(4a\sqrt 2 \) B. \(a\sqrt 2 \) C. \(3a\sqrt 2 \) D. \(2a\sqrt 2 \)
Câu 27: Cho tam giác ABC đều cạnh a, G là trọng tâm. Mệnh đề nào sau đây sai?
A. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}{a^2}.\) B. \(\overrightarrow {AC} .\overrightarrow {CB} = - \frac{1}{2}{a^2}.\) C. \(\overrightarrow {GA} .\overrightarrow {GB} = \frac{1}{6}{a^2}.\) D. \(\overrightarrow {AB} .\overrightarrow {AG} = \frac{1}{2}{a^2}.\)
Câu 28: Cho bốn điểm A,B,C,D phân biệt. Khi đó, \(\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} - \overrightarrow {AD} \) bằng véctơ nào sau đây?
A. \(\vec 0\) B. \(\overrightarrow {BD} \) C. \(\overrightarrow {AC} \) D. \(2\overrightarrow {DC} \)
Câu 29: Cho hình chữ nhật ABCD. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AC} {\rm{ \;}} = \overrightarrow {BD} \) B. \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \vec 0\)
C. \(\left| {\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AD} } \right|\) D. \(\left| {\overrightarrow {BC} {\rm{ \;}} + \overrightarrow {BD} } \right| = \left| {\overrightarrow {AC} {\rm{ \;}} - \overrightarrow {AB} } \right|\)
Câu 30: Cho tam giác ABC có trung tuyến BM và trọng tâm \(G\). Đặt \(\overrightarrow {BC} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BA} {\rm{\;}} = b\). Hãy phân tích vectơ \(\overrightarrow {BG} \) theo \(\vec a\) và \(\vec b\).
A. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\) B. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{2}{3}\vec b\) C. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{2}{3}\vec b\) D. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{1}{3}\vec b\)
II. Tự luận (4 điểm)
Câu 1: Cho ba lực \(\overrightarrow {{F_1}} {\rm{\;}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} {\rm{\;}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} {\rm{\;}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ lực \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M . Tìm hướng và cường độ lực \(\overrightarrow {{F_3}} \)
Câu 2: Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách \(AB = 12m\) , cùng thẳng hàng với chân C của tháp để đặt giác kế. Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm \({A_1},{B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao CD của tháp. Người ta đo được \(\widehat {D{A_1}{C_1}} = {49^ \circ }\) và \(\widehat {D{B_1}{C_1}} = {35^ \circ }\). Tính chiều cao CD của tháp đó.
Câu 3: Tìm parabol (P) \(y = a{x^2} + bx + c\) biết (P) có đỉnh \(I(2;3)\) và giao với Oy tại điểm có tung độ bằng -1. Vẽ đồ thị hàm số tìm được.
-----HẾT-----
Lời giải
I. Trắc nghiệm (6 điểm)
|
1. C |
2. C |
3. C |
4. C |
5. B |
6. D |
7.A |
8. D |
|
9. A |
10. D |
11. A |
12. C |
13. B |
14. C |
15. D |
16. C |
|
17. B |
18. A |
19. D |
20. B |
21. D |
22. C |
23. D |
24. C |
|
25. C |
26. D |
27. C |
28. A |
29.A |
30. A |
Câu 1 (NB):
Phương pháp:
- \(\sqrt {P(x)} \) có nghĩa khi \(P(x) \ge 0\).
- \(\frac{{Q(x)}}{{\sqrt {P(x)} }}\) có nghĩa khi \(P(x) > 0\).
Cách giải:
Hàm số \(y = \sqrt {6 - 3x} + \frac{1}{{\sqrt {x - 1} }}\) xác định khi \(\left\{ \begin{array}{l}6 - 3x \ge 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\x > 1\end{array} \right. \Leftrightarrow 1 < x \le 2\)
Vậy tập xác định \(D = (1;2]\)
Chọn C.
Câu 2 (TH):
Phương pháp:
Phủ định của mệnh đề “\(\forall x \in K,\,\,P\left( x \right)\)” là mệnh đề “\(\exists x \in K,\,\,\overline {P\left( x \right)} \)”.
Cách giải:
Mệnh đề phủ định của mệnh đề P(x): “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)” là “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”.
Chọn C.
Câu 3 (TH):
Phương pháp:
Thay tọa độ các điểm vào hàm số
Cách giải:
Với \(x = 6,x = 0\)thì \(y = \frac{{\sqrt {x - 2} - 2}}{{x - 6}}\) không xác định. Suy ra điểm \((6;0)\) và \((0;6)\)không thuộc đồ thị hàm số
Với \(x = 2\) thì \(y = \frac{{\sqrt {2 - 2} - 2}}{{2 - 6}} = 0,5 \ne - 0,5\). Suy ra điểm \((2; - 0,5)\)không thuộc đồ thị hàm số, điểm \((2;0,5)\) thuộc đồ thị hàm số
Chọn C.
Câu 4 (TH):
Phương pháp:
Tập hợp rỗng không chứa phần tử nào.
Cách giải:
+) Xét đáp án A: \(\left\{ {\begin{array}{*{20}{l}}{x \in \mathbb{R}}\\{\left| x \right| < 1}\end{array}} \right. \Rightarrow {\rm{\;}} - 1 < x < 1\) \( \Rightarrow A = \left( { - 1;{\mkern 1mu} {\mkern 1mu} 1} \right) \ne \emptyset \)
\( \Rightarrow \) Loại đáp án A.
+) Xét đáp án B: \(6{x^2} - 7x + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = \frac{1}{6}}\end{array}} \right.\) \( \Rightarrow A = \left\{ 1 \right\} \ne \emptyset \)
\( \Rightarrow \) Loại đáp án B.
+) Xét đáp án C: \({x^2} - 4x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2 + \sqrt 2 }\\{x = 2 - \sqrt 2 }\end{array}} \right.\) \( \Rightarrow A = \emptyset \)
Chọn C.
Câu 5 (VD):
Phương pháp:
Thực hiện các phép toán trên tập hợp. Sử dụng trục số.
Cách giải:
+) \(A \cap B = \left( { - 3;2} \right]\)
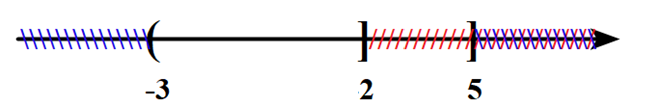
=> A đúng.
+) \(A\backslash B = \left( { - \infty ; - 3} \right]\)

=> B sai.
+) \(A \cup B = \left( { - \infty ;5} \right]\)
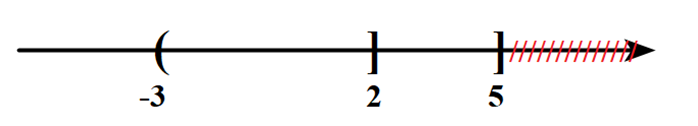
=> C đúng.
+) \(B\backslash A = \left( {2;5} \right]\).
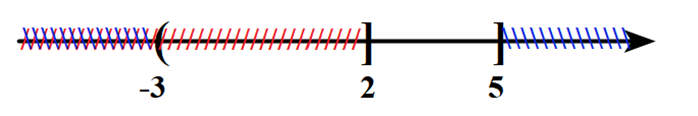
=> D đúng.
Chọn B.
Câu 6 (TH):
Phương pháp:
Cho tập hợp B có n phần tử. Số tập hợp con của B là \({2^n}\)
Cách giải:
Tập hợp \(B = \left\{ {x;{\mkern 1mu} {\mkern 1mu} y;{\mkern 1mu} {\mkern 1mu} z;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 5} \right\}\) có 5 phần tử.
Số tập hợp con của tập B là: \({2^5} = 32\)
Chọn D.
Câu 7 (NB):
Cách giải:
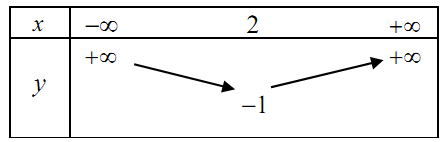
Với \(a > 0\), ta có bảng biến thiên

Hàm số nghịch biến trên \(\left( { - \infty ;\, - \frac{b}{{2a}}} \right).\)
Chọn A.
Câu 8 (TH):
Phương pháp:
Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là \(ax + by + c < 0\), \(ax + by + c > 0\), \(ax + by + c \le 0\), \(ax + by + c \ge 0\), trong đó a, b, c là các số cho trước sao cho \({a^2} + {b^2} \ne 0\).
Cách giải:
Bất phương trình bậc nhất hai ẩn là \(x + y \ge 0\).
Chọn D.
Câu 9 (TH):
Phương pháp:
Thay tọa độ các điểm ở các đáp án vào bất phương trình.
Cách giải:
Thay tọa độ điểm A(1;-1) ta có: \(\left( {1 + \sqrt 3 } \right) + \left( {1 - \sqrt 3 } \right) = 2 \ge 2\) (Đúng).
Vậy điểm A thuộc miền nghiệm của bất phương trình.
Chọn A.
Câu 10 (NB):
Phương pháp:
Sử dụng định lí cosin trong tam giác: \({a^2} = {b^2} + {c^2} - 2bc.\cos A.\)
Cách giải:
\(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos G\) là mệnh đề đúng.
Chọn D.
Câu 11 (VD):
Cách giải:
Ta có:
\(AC = BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \)
Lại có:
\(\left\{ \begin{array}{l}\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{1}{2}\overrightarrow {AD} \\\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \end{array} \right.\)
\(\begin{array}{l} \Rightarrow \overrightarrow {BK} .\overrightarrow {AC} = \left( {\overrightarrow {BA} + \frac{1}{2}\overrightarrow {AD} } \right).\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\\ = \overrightarrow {BA} .\overrightarrow {AB} + \overrightarrow {BA} .\overrightarrow {AD} + \frac{1}{2}\overrightarrow {AD} .\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} .\overrightarrow {AD} \\ = - {a^2} + 0 + 0 + \frac{1}{2}{\left( {a\sqrt 2 } \right)^2}\\ = 0\end{array}\)
Chọn A.
Câu 12 (VD):
Phương pháp:
Tính sinA.
Tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\)
Sử dụng định lí cosin trong tam giác tính a: \({a^2} = {b^2} + {c^2} - 2bc.\cos A.\)
Sử dụng công thức tính diện tích tam giác: \(S = \frac{1}{2}a{h_a}\), từ đó tính \({h_a}\).
Cách giải:
Ta có:
\(\begin{array}{l}{\sin ^2}A + {\cos ^2}A = 1\\ \Leftrightarrow {\sin ^2}A + {\left( {\frac{3}{5}} \right)^2} = 1\\ \Leftrightarrow {\sin ^2}A = \frac{{16}}{{25}}\end{array}\)
Vì \({0^0} < A < {180^0}\) nên sinA > 0 \( \Rightarrow \sin A = \frac{4}{5}.\)
Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A. = \frac{1}{2}.7.5.\frac{4}{5} = 14.\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A.\\\,\,\,\,\,\, = {7^2} + {5^2} - 2.7.5.\frac{3}{5}\\\,\,\,\,\,\, = 32\\ \Rightarrow a = 4\sqrt 2 .\end{array}\)
Lại có: \(S = \frac{1}{2}a{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2.14}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}.\)
Chọn C.
Câu 13 (TH):
Cách giải:
Hàm số bậc hai cần tìm có phương trình: \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Hàm số bậc hai có đồ thị là parabol có đỉnh là \(S\left( {\frac{5}{2};\frac{1}{2}} \right)\)và đi qua \(A\left( {1; - 4} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = \frac{5}{2}\\a.\frac{{25}}{4} + b.\frac{5}{2} + c = \frac{1}{2}\\a + b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{ - b}}{a} = 5\\25a + 10b + 2c = 2\\a + b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5{\rm{a + b = 0}}\\25a + 10b + 2c = 2\\a + b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = 10\\c = - 12\end{array} \right.\)
Chọn B.
Câu 14 (TH):
Phương pháp:
Thay tọa độ các điểm vào hệ bất phương trình.
Cách giải:
Dễ thấy các điểm \(O\left( {0;0} \right)\), \(M\left( {1;0} \right)\), \(P\left( {0;2} \right)\) không thỏa mãn bất phương trình \(x + y + 1 < 0\) nên không thỏa mãn cả hệ bất phương trình.
Chọn C.
Câu 15 (TH):
Cách giải:
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, - 1} \right)\) nên \(c = - 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, - 3} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 1\\a{.1^2} + b.1 - 1 = - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 4\end{array} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} - 4x - 1\).
Chọn D.
Câu 16 (TH):
Phương pháp:
Sử dụng công thức tính diện tích tam giác \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = pr\).
Cách giải:
Nửa chu vi tam giác đều cạnh a là \(p = \frac{{a + a + a}}{2} = \frac{{3a}}{2}\).
Tam giác đều cạnh a có diện tích \(S = \sqrt {\frac{{3a}}{2}\left( {\frac{{3a}}{2} - a} \right)\left( {\frac{{3a}}{2} - a} \right)\left( {\frac{{3a}}{2} - a} \right)} = \frac{{{a^2}\sqrt 3 }}{4}\).
Lại có \(S = pr \Leftrightarrow r = \frac{S}{p} = \frac{{{a^2}\sqrt 3 }}{4}:\frac{{3a}}{2} = \frac{{a\sqrt 3 }}{6}\).
Chọn C.
Câu 17 (NB):
Phương pháp:
Sử dụng hệ quả định lí Cosin trong tam giác: \(\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2AC.BC}}\).
Cách giải:
Áp dụng hệ quả định lí Cosin trong tam giác ABC ta có:
\(\begin{array}{l}\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2AC.BC}}\\ \Leftrightarrow \cos {45^0} = \frac{{{{\left( {\sqrt 3 } \right)}^2} + B{C^2} - {{\left( {\sqrt 2 } \right)}^2}}}{{2.\sqrt 3 .BC}}\\ \Leftrightarrow \sqrt 6 BC = B{C^2} + 1\\ \Leftrightarrow B{C^2} - \sqrt 6 BC + 1 = 0\\ \Leftrightarrow BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}\end{array}\).
Chọn B.
Câu 18 (TH):
Phương pháp:
Số chính phương có các chữ số tận cùng là \(0,{\rm{ }}1,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}9\). Dùng loại trừ để đưa ra đáp án đúng.
Cách giải:
Hàm số \(y = - {x^2} + 2x - 1\) có \(a = - 1 < 0\), nên loại C,D.
Hoành độ đỉnh \({x_I} = - \frac{b}{{2a}} = - \frac{2}{{2.( - 1)}} = 1\)
Chọn A.
Câu 19 (NB):
Phương pháp:
Biểu diễn tập hợp trên trục số.
Cách giải:
Hình vẽ đã cho là minh họa cho tập hợp \(( - 3;5]\)
Chọn D.
Câu 20 (VD):
Cách giải:
Ta có \( - \frac{b}{{2a}} = \frac{1}{3}\) và \(a = - 3 < 0\). Suy ra hàm số đã cho nghịch biến trên khoảng \(\left( {\frac{1}{3}; + \infty } \right)\).
Mà \(\left[ {1;3} \right] \subset \left( {\frac{1}{3}; + \infty } \right)\).
Do đó trên đoạn \(\left[ {1;3} \right]\) hàm số đạt giá trị lớn nhất tại \(x = 1\), tức là \(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = f\left( 1 \right) = 0\).
Chọn B.
Câu 21 (TH):
Phương pháp:
Áp dụng công thức \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)
Cách giải:
Ta có \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 3}}{{3.2}} = - \frac{1}{2}\)
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {120^o}\)
Chọn D.
Câu 22 (VD):
Phương pháp:
- Tính BC dựa vào định lí côsin trong tam giác cân ABC.
- Tính BM.
- Tính AM dựa vào định lí côsin trong tam giác ABM.
Cách giải:
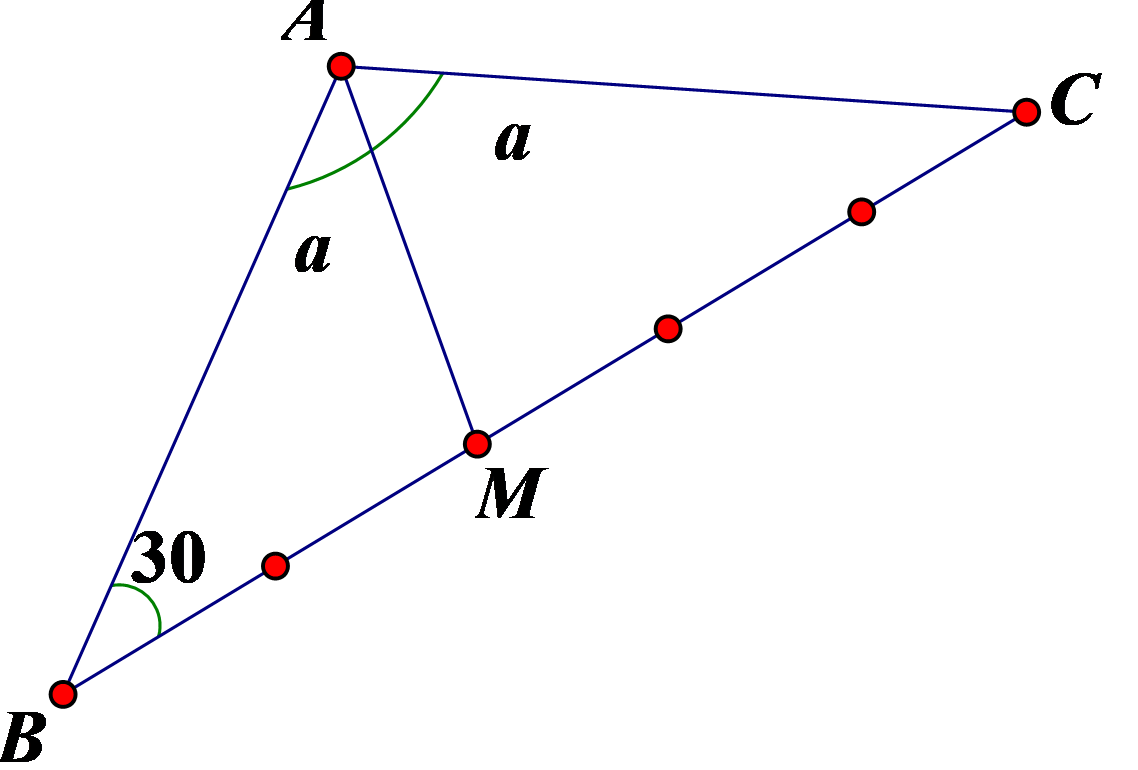
\(BC = \sqrt {A{B^2} + A{C^2} - 2ABAC\cos {{120}^0}} = \sqrt {{a^2} + {a^2} - 2a.a.\left( { - \frac{1}{2}} \right)} = a\sqrt 3 {\rm{ }} \Rightarrow BM = \frac{{2a\sqrt 3 }}{5}\)
\(AM = \sqrt {A{B^2} + B{M^2} - 2AB.BM.cos{{30}^0}} = \sqrt {{a^2} + {{\left( {\frac{{2a\sqrt 3 }}{5}} \right)}^2} - 2a.\frac{{2a\sqrt 3 }}{5}.\frac{{\sqrt 3 }}{2}} = \frac{{a\sqrt 7 }}{5}\).
Chọn C.
Câu 23 (TH):
Phương pháp:
Tìm phương trình đường thẳng d. Loại đáp án.
Thay tọa độ điểm O(0;0) vào các bất phương trình chưa bị loại ở các đáp án, tiếp tục loại đáp án.
Cách giải:
Đường thẳng d đi qua điểm (3;0) nên loại đáp án A, B.
Ta thấy điểm O(0;0) không thuộc miền nghiệm của bất phương trình.
+ Thay tọa độ điểm O(0;0) vào biểu thức \(x - 2y\) ta có: \(0 - 2.0 = 0 < 3\)
Do đó bất phươn trình cần tìm là \(x - 2y > 3\)
Chọn D.
Câu 24 (TH):
Phương pháp:
Sử dụng công thức: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}.\)
Cách giải:
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow 1 + {\left( { - 2\sqrt 2 } \right)^2} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\cos ^2}\alpha = \frac{1}{9}\\ \Leftrightarrow {\sin ^2}\alpha = 1 - \frac{1}{9} = \frac{8}{9}\\ \Leftrightarrow \sin \alpha = \pm \frac{{2\sqrt 2 }}{3}\end{array}\)
Vì \({0^0} < \alpha < {180^0}\) \( \Rightarrow \sin \alpha > 0\).
Vậy \(\sin \alpha = \frac{{2\sqrt 2 }}{3}.\)
Chọn C.
Câu 25 (VD):
Phương pháp:
Áp dụng hệ quả định lí Sin trong tam giác ABC.
Cách giải:
Ta có: \(\angle ACB = {180^0} - {45^0} - {70^0} = {65^0}\)
Áp dụng hệ quả định lí Sin trong tam giác ABC ta có:
\(\begin{array}{l}\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{AC}}{{\sin {{70}^0}}} = \frac{{40}}{{\sin {{65}^0}}}\\ \Rightarrow AC = \frac{{40}}{{\sin {{65}^0}}}.\sin {70^0} \approx 41,47\,\,\left( m \right)\end{array}\)
Chọn C.
Câu 26 (VD):
Phương pháp:
Áp dụng quy tắc cộng vecto để tìm được vecto \(\vec u\).
Cách giải:
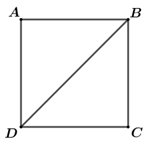
Vì ABCD là hình vuông nên ta có: \(AB = BC = CD = DA = 2\); \(AC = BD = a\sqrt 2 \).
Ta có:
\(\vec u = \overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {MC} {\rm{\;}} - 3\overrightarrow {MD} \)
\({\mkern 1mu} = \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DA} } \right) + \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DB} } \right) + \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DC} } \right) - 3\overrightarrow {MD} \)
\({\mkern 1mu} = \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DA} {\rm{\;}} + \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DB} {\rm{\;}} + \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DC} {\rm{\;}} - 3\overrightarrow {MD} \)
\( = \overrightarrow {DA} {\rm{\;}} + \overrightarrow {DB} {\rm{\;}} + \overrightarrow {DC} \)
\( = \left( {\overrightarrow {DA} {\rm{\;}} + \overrightarrow {DC} } \right) + \overrightarrow {DB} \)
\( = \overrightarrow {DB} {\rm{\;}} + \overrightarrow {DB} \)
\( = 2\overrightarrow {DB} \)
\( \Rightarrow \vec u = 2\overrightarrow {DB} \)
\( \Rightarrow \left| {\vec u} \right| = \left| {2.\overrightarrow {DB} } \right| = 2.a.\sqrt 2 {\rm{\;}} = 2\sqrt 2 a\)
Chọn D.
Câu 27 (VD):
Phương pháp:
Áp dụng tích vô hướng \(\overrightarrow a .\overrightarrow b = a.b.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
Cách giải:
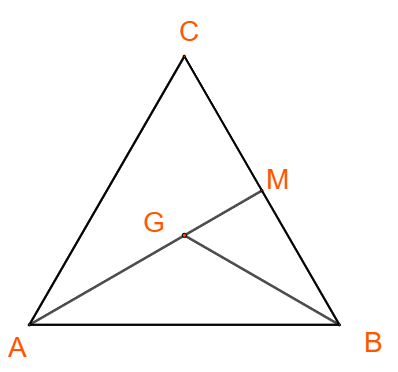
Ta có:
\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a.\cos A = {a^2}\cos {60^ \circ } = \frac{1}{2}{a^2}\) => A đúng
\(\overrightarrow {AC} .\overrightarrow {CB} = AC.CB.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a.a.\cos {120^ \circ } = - \frac{1}{2}{a^2}\) => B đúng
+ \(AG = \frac{2}{3}AM;AM = AC.\sin C = a.\sin {60^ \circ } = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AG = BG = \frac{{a\sqrt 3 }}{3}\)
\(\overrightarrow {GA} .\overrightarrow {GB} = GA.GB.\cos \left( {\overrightarrow {GA} ,\overrightarrow {GB} } \right) = \frac{{a\sqrt 3 }}{3}.\frac{{a\sqrt 3 }}{3}.\cos {120^ \circ } = - \frac{1}{6}{a^2}\) => C sai.
\(\overrightarrow {AB} .\overrightarrow {AG} = AB.AG.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AG} } \right) = a.\frac{{a\sqrt 3 }}{3}.\cos {30^ \circ } = \frac{1}{2}{a^2}\) => D đúng.
Chọn C.
Câu 28 (NB):
Phương pháp:
Nhóm \(\overrightarrow {AB} ,\overrightarrow {BC} \); \(\overrightarrow {DC} ,\overrightarrow {AD} \), áp dụng quy tắc cộng vectơ.
Cách giải:
Ta có: \(\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} - \overrightarrow {AD} {\rm{ \;}} = \left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right) - \left( {\overrightarrow {AD} {\rm{ \;}} + \overrightarrow {DC} } \right) = \overrightarrow {AC} {\rm{ \;}} - \overrightarrow {AC} {\rm{ \;}} = \vec 0\).
Chọn A.
Câu 29 (NB):
Phương pháp:
Sử dụng quy tắc hình bình hành tính \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} \).
Tính độ dài vectơ vừa tìm được.
Cách giải:
Ta có: \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\).
Chọn A.
Câu 30 (TH):
Phương pháp:
Áp dụng quy tắc cộng vecto, quy tắc hình bình hành để biểu diễn véctơ.
Cách giải:
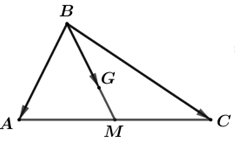
\(\overrightarrow {BM} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {BC} } \right) = \frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\overrightarrow {BM} {\rm{\;}} = \frac{2}{3} \cdot \left( {\frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} } \right) = \frac{1}{3}\overrightarrow {BA} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \)
Mặt khác, \(\overrightarrow {BA} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BC} {\rm{\;}} = \vec b\) nên ta có: \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\)
Vậy \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\).
Chọn A.
II. Tự luận (3 điểm)
Câu 1 (VD):
Phương pháp:
Áp dụng quy tắc hình bình hành.
Vật đứng yên khi tổng các lực tác động lên điểm bằng 0.
Cách giải:
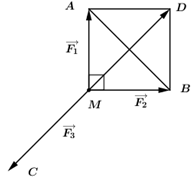
Có cường độ lực \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M
\( \Rightarrow \) Tam giác MAB vuông cân tại M
Lấy điểm D sao cho MADB là hình vuông
\( \Rightarrow MD = \sqrt {M{A^2} + A{D^2}} {\rm{\;}} = \sqrt {M{A^2} + M{B^2}} {\rm{\;}} = 50\sqrt 2 {\mkern 1mu} {\mkern 1mu} N\)
Vì vật đứng yên nên tổng các lực tác động lên điểm bằng 0
\( \Rightarrow \overrightarrow {{F_1}} {\rm{\;}} + \overrightarrow {{F_2}} {\rm{\;}} + \overrightarrow {{F_3}} {\rm{\;}} = \vec 0\) hay \(\overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {{F_3}} {\rm{\;}} = \vec 0\)
\( \Rightarrow \overrightarrow {{F_3}} {\rm{\;}} = {\rm{\;}} - \left( {\overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} } \right) = {\rm{\;}} - \overrightarrow {MD} \)
Vậy lực \(\overrightarrow {{F_3}} \) có hướng ngược với \(\overrightarrow {MD} \) và có cường độ bằng \(50\sqrt 2 {\mkern 1mu} {\mkern 1mu} N \approx 70,71{\mkern 1mu} {\mkern 1mu} N\)
Câu 2 (VD):
Cách giải:
Ta có: \(\widehat {D{A_1}B} = {180^ \circ } - {49^ \circ } = {131^ \circ };\widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lý sin trong tam giác \(D{A_1}{B_1}\) ta có:
\(\begin{array}{l}\frac{{{A_1}{B_1}}}{{\sin \widehat {{A_1}D{B_1}}}} = \frac{{D{B_1}}}{{\sin \widehat {D{A_1}{B_1}}}} \Leftrightarrow \frac{3}{{\sin {{14}^ \circ }}} = \frac{{D{B_1}}}{{\sin {{131}^ \circ }}}\\ \Rightarrow D{B_1} = \sin {131^ \circ }.\frac{3}{{\sin {{14}^ \circ }}}\end{array}\)
Lại có: \(\Delta D{C_1}{B_1}\) vuông tại \({C_1}\) nên \(D{C_1} = D{B_1}.\sin {B_1} = D{B_1}.\sin {35^ \circ }\)
\( \Rightarrow D{C_1} = \sin {131^ \circ }.\frac{3}{{\sin {{14}^ \circ }}}.\sin {35^ \circ } \approx 5,37\)
Chiều cao CD của tháp là \(5,37 + 2 = 7,37(m)\)
Vậy tháp cao khoảng 7,37m.
Câu 3 (VD):
Cách giải:
Parabol (P) \(y = a{x^2} + bx + c\) giao với Oy tại điểm có tọa độ \((0;c)\), do đó \(c = - 1\)
(P) có hoành độ đỉnh \({x_I} = - \frac{b}{{2a}} = 2 \Rightarrow b = - 4a\)
Điểm \(I(2;3)\) thuộc (P) nên \(a{.2^2} + b.2 - 1 = 3\) hay \(4a + 2b = 4\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}4a + 2b = 4\\b = - 4a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4\\a = - 1\end{array} \right.\)
Vậy parabol cần tìm là \(y = - {x^2} + 4x - 1\)
* Vẽ parabol
Đỉnh \(I(2;3)\)
Trục đối xứng \(x = 2\)
Giao với Oy tại A(0;-1), lấy điểm B(4;-1) đối xứng với A qua trục đối xứng
Lấy điểm C(1;2) và D(3;2) thuộc đồ thị.