Đề thi học kì 1 Toán 6 - Đề số 12 - Cánh diều
Phần trắc nghiệm (3 điểm) Câu 1: Cho tập hợp M = {x ∈ N| 15 < x ≤ 20}. Hãy chọn khẳng định đúng:
Đề bài
Cho tập hợp M = {x ∈ N| 15 < x ≤ 20}. Hãy chọn khẳng định đúng:
-
A.
M = {15; 16; 17; 18; 19} .
-
B.
M = {15; 16; 17; 18;19; 20}.
-
C.
M = {16; 17; 18; 19}.
-
D.
M = {16; 17; 18; 19; 20}.
Số nào trong các số sau không là số nguyên tố?
-
A.
2 .
-
B.
8.
-
C.
5.
-
D.
7.
Kết quả của phép tính 2 4 : 2 bằng
-
A.
2 .
-
B.
4.
-
C.
8.
-
D.
16.
Tìm các số nguyên âm trong các số sau: -5; 17; 0; -11; 12
-
A.
-5; 17; -11; 12 .
-
B.
17; 12.
-
C.
-5; -11.
-
D.
-5; 0; -11.
Sắp xếp các số sau theo thứ tự giảm dần: -17; 30; - 29; -3; 14; 0; 24; -43. Kết quả đúng là:
-
A.
-43; -29; -17; -3; 0; 14; 24; 30.
-
B.
30; 24; 14; 0; -3; -17; -29; -43.
-
C.
0; -3; -17; 14; 24; -29;30; -43.
-
D.
-43; 24; -29; 14; -17; 30; -3; 0.
Kết quả của phép tính 59 – 70 là
-
A.
11.
-
B.
-11.
-
C.
-129.
-
D.
129.
Chọn phát biểu sai ?
-
A.
Hình vuông có bốn cạnh bằng nhau.
-
B.
Hình vuông có bốn cặp cạnh đối song song.
-
C.
Hình vuông có hai đường chéo bằng nhau.
-
D.
Hình vuông có bốn góc bằng nhau.
Có bao nhiêu tính chất dưới đây là tính chất của hình thang cân?
a) Trong hình thang cân có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
b) Trong hình thang cân có hai đường chéo bằng nhau.
c) Trong hình thang cân có hai góc kề một đáy bằng nhau.
d) Trong hình thang cân có hai cặp cạnh đối song song với nhau.
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Kết luận nào sau đây không phải tính chất của hình thoi:
-
A.
Hai đường cắt nhau tại trung điểm của mỗi đường.
-
B.
Bốn góc bằng nhau.
-
C.
Bốn cạnh bằng nhau.
-
D.
Hai đường chéo vuông góc.
-
A.
Hình chữ nhật vừa có trục đối xứng, vừa có tâm đối xứng.
-
B.
Hình chữ nhật chỉ có trục đối xứng
-
C.
Hình chữ nhật chỉ có tâm đối xứng.
-
D.
Hình chữ nhật không có trục đối xứng, không có tâm đối xứng.
-
A.
Tam giác đều.
-
B.
Cánh quạt.
-
C.
Trái tim.
-
D.
Cánh diều.
-
A.
Biển d.
-
B.
Biển c.
-
C.
Biển b.
-
D.
Biển a.
Lời giải và đáp án
Cho tập hợp M = {x ∈ N| 15 < x ≤ 20}. Hãy chọn khẳng định đúng:
-
A.
M = {15; 16; 17; 18; 19} .
-
B.
M = {15; 16; 17; 18;19; 20}.
-
C.
M = {16; 17; 18; 19}.
-
D.
M = {16; 17; 18; 19; 20}.
Đáp án : D
Dựa vào cách biểu diễn tập hợp.
M = {x ∈ N| 15 < x ≤ 20} = {16; 17; 18; 19; 20}.
Số nào trong các số sau không là số nguyên tố?
-
A.
2 .
-
B.
8.
-
C.
5.
-
D.
7.
Đáp án : B
Dựa vào kiến thức về số nguyên tố: Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó.
Ta có:
Ư(2) = {1; 2}
Ư(8) = {1; 2; 4; 8}
Ư(5) = {1; 5}
Ư(7) = {1; 7}
=> 8 không phải số nguyên tố.
Kết quả của phép tính 2 4 : 2 bằng
-
A.
2 .
-
B.
4.
-
C.
8.
-
D.
16.
Đáp án : C
Sử dụng quy tắc chia hai lũy thừa cùng cơ số
Ta có: \({2^4}:2 = {2^{4 - 1}} = {2^3} = 8\).
Tìm các số nguyên âm trong các số sau: -5; 17; 0; -11; 12
-
A.
-5; 17; -11; 12 .
-
B.
17; 12.
-
C.
-5; -11.
-
D.
-5; 0; -11.
Đáp án : C
Số nguyên âm được nhận biết bằng dấu “ – “ ở trước số tự nhiên khác 0.
Các số nguyên âm là: -5; -11.
Sắp xếp các số sau theo thứ tự giảm dần: -17; 30; - 29; -3; 14; 0; 24; -43. Kết quả đúng là:
-
A.
-43; -29; -17; -3; 0; 14; 24; 30.
-
B.
30; 24; 14; 0; -3; -17; -29; -43.
-
C.
0; -3; -17; 14; 24; -29;30; -43.
-
D.
-43; 24; -29; 14; -17; 30; -3; 0.
Đáp án : B
- So sánh các số với 0.
- So sánh các số nguyên âm với nhau, các số nguyên dương với nhau.
Ta có các số nguyên âm là: -17; -29; -3; -43.
Các số nguyên dương là: 30; 14; 24.
Vì 3 < 17 < 29 < 43 nên -3 > -17 > -29 > -43.
30 > 24 > 14.
Các số theo thứ tự giảm dần là: 30; 24; 14; 0; -3; -17; -29; -43.
Kết quả của phép tính 59 – 70 là
-
A.
11.
-
B.
-11.
-
C.
-129.
-
D.
129.
Đáp án : B
Sử dụng quy tắc trừ hai số nguyên.
Ta có: 59 – 70 = - (70 – 59) = - 11.
Chọn phát biểu sai ?
-
A.
Hình vuông có bốn cạnh bằng nhau.
-
B.
Hình vuông có bốn cặp cạnh đối song song.
-
C.
Hình vuông có hai đường chéo bằng nhau.
-
D.
Hình vuông có bốn góc bằng nhau.
Đáp án : B
Dựa vào kiến thức về hình vuông:
Một số yếu tố cơ bản của hình vuông
- Bốn cạnh bằng nhau.
- Bốn góc bằng nhau và bằng 90 0 .
- Hai đường chéo bằng nhau.
Hình vuông chỉ có hai cặp cạnh đối nên đáp án B sai.
Có bao nhiêu tính chất dưới đây là tính chất của hình thang cân?
a) Trong hình thang cân có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
b) Trong hình thang cân có hai đường chéo bằng nhau.
c) Trong hình thang cân có hai góc kề một đáy bằng nhau.
d) Trong hình thang cân có hai cặp cạnh đối song song với nhau.
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Đáp án : B
Dựa vào kiến thức về hình thang cân:
Hình thang cân có:
- Hai cạnh bên bằng nhau.
- Hai đường chéo bằng nhau
- Hai đáy song song với nhau
- Hai góc kề một đáy bằng nhau.
Trong các ý trên, các ý là tính chất của hình thang là: b, c.
Ý a sai vì hai đường chéo của hình thang cân không cắt nhau tại trung điểm của mỗi đường.
Ý d sai vì hình thang cân chỉ có hai đáy song song với nhau, hai cạnh bên không song song với nhau.
Kết luận nào sau đây không phải tính chất của hình thoi:
-
A.
Hai đường cắt nhau tại trung điểm của mỗi đường.
-
B.
Bốn góc bằng nhau.
-
C.
Bốn cạnh bằng nhau.
-
D.
Hai đường chéo vuông góc.
Đáp án : B
Dựa vào kiến thức về hình thoi:
Một số yếu tố cơ bản của hình thoi
- Bốn cạnh bằng nhau
- Hai đường chéo vuông góc với nhau.
- Các cạnh đối song song với nhau
- Các góc đối bằng nhau
Bốn góc của hình thoi không bằng nhau nên B sai.
-
A.
Hình chữ nhật vừa có trục đối xứng, vừa có tâm đối xứng.
-
B.
Hình chữ nhật chỉ có trục đối xứng
-
C.
Hình chữ nhật chỉ có tâm đối xứng.
-
D.
Hình chữ nhật không có trục đối xứng, không có tâm đối xứng.
Đáp án : A
Dựa vào kiến thức về trục đối xứng, tâm đối xứng của hình chữ nhật.
Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
=> Hình chữ nhật vừa có trục đối xứng, vừa có tâm đối xứng.
-
A.
Tam giác đều.
-
B.
Cánh quạt.
-
C.
Trái tim.
-
D.
Cánh diều.
Đáp án : B
Dựa vào kiến thức về hình có tâm đối xứng: Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Hình có tâm đối xứng là hình cánh quạt.

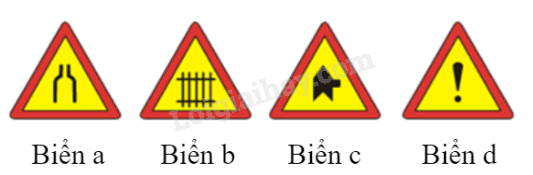
-
A.
Biển d.
-
B.
Biển c.
-
C.
Biển b.
-
D.
Biển a.
Đáp án : B
Dựa vào kiến thức về hình có trục đối xứng: Có một đường thẳng d chia hình thành hai phần mà khi ta “ gấp ” hình theo đường thẳng d thì hai phần đó “ chồng khít ” lên nhau .
Hình c không có trục đối xứng.

a) Sử dụng tính chất của phép cộng để tính hợp lí.
b) Sử dụng tính chất phân phối của phép nhân với phép trừ để tính hợp lí.
a) 125 + (- 45) + 2023 + 45 + (- 125)
= (125 – 125) + (-45 + 45) + 2023
= 0 + 0 + 2023
= 2023.
b) \({\rm{ 5}}1.74{\rm{ }}-{\rm{ 5}}1.70{\rm{ }} - 51.4\)
= 51.(74 – 70 – 4)
= 51.0
= 0.
Sử dụng các phép tính với số nguyên để tìm x.
a) 90 – x = 135
x = 90 – 135
x = - 45
Vậy x = - 45.
b) 158 – 5x = 258
5x = 158 – 258 = - 100
x = - 100: 5
x = -20
Vậy x = -20.
Gọi x là số học sinh khối 6. (học sinh) (x là BC(15; 18) và 400 < x < 500).
+ Tìm BCNN(15; 18).
+ BC(15; 18) là tập hợp bội của BCNN(15; 18).
+ Chọn trong số đó bội thỏa mãn điều kiện đã cho.
Gọi x là số học sinh khối 6 (học sinh) => 400 < x < 500 và x là BC( 15; 18)
Ta có: 15 = 3.5; 18 = 2.3 2 nên BCNN(15; 18) = 2.3 2 .5 = 90
BC (15; 18) = {0; 90; 180; 270; 360; 450; ....}
Vì 400 < x < 500 nên x = 450.
Vậy khối 6 có 450 học sinh.
Tính tổng số tiền thu được trong 1 năm của cả hai cửa hàng A và B.
Một năm có 12 tháng nên lấy tổng số tiền chia cho 12 ta được số tiền bình quân mỗi tháng của công ty từ hai cửa hàng.
Số tiền thu được trong 1 năm từ cửa hàng A và cửa hàng B là
425 + ( - 65) = 360 (triệu đồng)
Số tiền thu được mỗi tháng từ cửa hàng A và B là:
360 : 12 = 30 (triệu đồng)
Vậy bình quân mỗi tháng công ty lãi 30 triệu đồng từ hai cửa hàng đó.
- Dựa vào tính chất của hình lục giác đều.
- Dựa vào tính chất tâm đối xứng để tính khoảng cách từ tâm đối xứng đến mỗi đỉnh của hình lục giác.
- Tính chu vi hình lục giác.
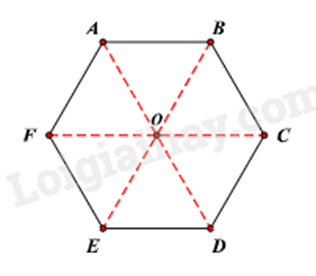
Gọi O là tâm đối xứng của mặt bàn.
Khoảng cách giữa tâm O đến mỗi đỉnh của mặt bàn hình lục giác đều là: OA = 1,2 : 2 = 0,6 (m).
Tam giác OAB là tam giác đều nên cạnh của hình lục giác đều là: AB = OA = 0,6m.
Chu vi của mặt bàn hình lục giác đều là: 0,6 . 6 = 3,6 (m).
Vậy chu vi của mặt bàn là 3,6 m.
Tính độ dài đáy lớn và chiều cao của thửa ruộng.
Sử dụng công thức tính diện tích hình thang để tính diện tích thửa ruộng.
Tính số kg thóc thu được.
Đáy lớn của thửa ruộng hình thang là:
26 + 8 = 34 (m)
Chiều cao của thửa ruộng hình thang là:
26 – 6 = 20 (m)
Diện tích thửa ruộng hình thang là:
(34 + 26).20: 2 = 600 (m 2 )
Vì trung bình cứ 100m 2 thu hoạch được 70kg thóc nên số ki-lô-gam thóc thu hoạch được trên thửa ruộng đó:
600 : 100 . 70 = 420 (kg)
Vậy thu hoạch được 420 kg thóc trên thửa ruộng đó.