Đề thi học kì 2 Toán 7 - Đề số 13 - Chân trời sáng tạo — Không quảng cáo

Dựa vào kiến thức về tính chất dãy tỉ số bằng nhau.

Ta có: $\frac{a}{b} = \frac{c}{d} = \frac{{a - c}}{{b - d}}$ nên C đúng.

Đáp án C.

Dựa vào tính chất tỉ lệ thức:

Nếu ad = bc và $a,b,c,d \ne 0$ thì ta có các tỉ lệ thức:

$\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{d}{b} = \frac{c}{a};\frac{d}{c} = \frac{b}{a}$.

Với 3.4 = 6.2 ta có các tỉ lệ thức sau:

$\frac{3}{2} = \frac{6}{4};\frac{3}{6} = \frac{2}{4};\frac{2}{3} = \frac{4}{6};\frac{6}{3} = \frac{4}{2}$.

Đáp án A.

Đơn thức là biểu thức đại số có dạng tích của một số thức với một lũy thừa của một biến.

Trong các biểu thức trên, các đơn thức là: $2x$; $5{x^6}$; $5xy$.

Vậy có 3 đơn thức.

Đáp án A.

Bậc của hạng tử có bậc cao nhất là bậc của đa thức.

Bậc của đa thức $3{x^3} - 5{x^2} + 17x - 29$ là 3 vì $3{x^3}$ có bậc lớn nhất (bậc là 3)

Đáp án D.

Đa thức một biến là tổng của những đơn thức của cùng một biến.

Đa thức ${x^3} - 6{x^2} + 9$ là đa thức một biến với biến là x.

Đáp án B.

Để nhân hai đơn thức ta nhân hay hệ số với nhau và nhân hai lũy thừa của biến với nhau.

Ta có: $7{x^2}.3x = 21{x^3}$.

Đáp án B.

Liệt kê các kết quả có thể xảy ra.

Khi rút bất kì một cây bút màu thì có 5 kết quả có thể xảy ra, đó là: màu cam, màu vàng, màu đỏ, màu hồng, màu xanh.

Đáp án D.

Xác suất xuất hiện mặt 4 chấm bằng tỉ số giữa số lần xuất hiện mặt 4 chấm với tổng số lần gieo xúc xắc.

Xác suất xuất hiện mặt $4$ chấm là: $\frac{3}{8}$.

Đáp án B.

Dựa vào tính chất của trọng tâm.

Vì D là trung điểm của BC nên AD là đường trung tuyến của tam giác ABC.

G là trọng tâm của $\Delta ABC$ nên $AG = \frac{2}{3}AD$ hay $\frac{{AG}}{{AD}} = \frac{2}{3}$.

Do đó: $\frac{{GD}}{{AD}} = \frac{{AD - AG}}{{AD}} = 1 - \frac{{AG}}{{AD}} = 1 - \frac{2}{3} = \frac{1}{3}$.

Đáp án A.

Dựa vào kiến thức đường vuông góc và đường xiên.

Đường vuông góc kẻ từ $A$ đến $MQ$ là $AI$ nên A đúng.

Đáp án A.

Chứng minh tam giác ABC cân tại A.

Dựa vào định lí tổng ba góc của một tam giác bằng ${180^0}$ để tính các góc của tam giác ABC.

Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A. (1)

Suy ra $\widehat B = \widehat C$.

Áp dụng định lí tổng ba góc của một tam giác bằng ${180^0}$ vào tam giác ABC, ta có:

$\widehat A + \widehat B + \widehat C = {180^o}$.

Mà $\widehat A = 2\widehat B$, $\widehat B = \widehat C$ nên $2\widehat B + \widehat B + \widehat B = {180^o}$

$4\widehat B = {180^0}$ suy ra $\widehat B = {180^0}:4 = {45^0}$

Suy ra $\widehat A = {2.45^0} = {90^0}$ nên tam giác ABC vuông tại A. (2)

Từ (1) và (2) suy ra tam giác ABC vuông cân tại A.

Đáp án D.

Dựa vào trường hợp bằng nhau cạnh huyền – góc nhọn của hai tam giác.

Để $\Delta ABC = \Delta DEF$ theo trường hợp cạnh huyền góc nhọn thì BC = EF và $\widehat B = \widehat E$ hoặc $\widehat C = \widehat F$.

Vậy ta chọn đáp án B.

Đáp án B.

Gọi số quyển vở ba lớp ủng hộ được lần lượt là a,b,c ( $a,b,c \in N*$).

Viết các biểu thức theo a, b, c.

Áp dụng tính chất dãy tỉ số bằng nhau để tìm a, b, c.

Gọi số quyển vở ba lớp ủng hộ được lần lượt là a,b,c ( $a,b,c \in N*$).

Theo đề bài ta có: $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ và $a + b + c = 360$

Áp dụng tính chất dãy tỉ số bằng nhau:

$\frac{a}{2} = \frac{b}{3} = \frac{c}{4}{\rm{ = }}\frac{{a + b + c}}{9} = \frac{{360}}{9} = 40$

$\Rightarrow \left\{ \begin{array}{l}\\\\\end{array} \right.$$\begin{array}{*{20}{l}}{a{\rm{ }} = 40.2{\rm{ }} = {\rm{ }}80}\\{b{\rm{ }} = {\rm{ 40}}.3{\rm{ }} = {\rm{ 120}}}\\{c{\rm{ }} = {\rm{ 40}}.4{\rm{ }} = {\rm{ 160}}}\end{array}$

Vậy số quyển vở ba lớp 7A, 7B, 7C ủng hộ được lần lượt là 80, 120, 160.

a) Dựa vào kiến thức về bậc, hạng tử tự do, hạng tử cao nhất để trả lời.

b) Áp dụng quy tắc cộng, trừ đa thức một biến để tìm B(x).

c) Áp dụng quy tắc chia đa thức để tính.

a) Bậc của đa thức là 2.

Hạng tử tự do là 1.

Hạng tử cao nhất của đa thức là 4.

b) Ta có: $A\left( x \right) + B\left( x \right) = 5{x^2} + 5x + 1$

$\begin{array}{l}B\left( x \right) = \left( {5{x^2} + 5x + 1} \right) - \left( {4{x^2} + 4x + 1} \right)\\ = 5{x^2} + 5x + 1 - 4{x^2} - 4x - 1\\ = \left( {5{x^2} - 4{x^2}} \right) + \left( {5x - 4x} \right) + \left( {1 - 1} \right)\\ = {x^2} + x\end{array}$

Vậy $B\left( x \right){\rm{ }} = {x^2} + x$

c) Ta có: $A\left( x \right):\left( {2x + 1} \right) = \left( {4{x^2} + 4x + 1} \right):\left( {2x + 1} \right)$

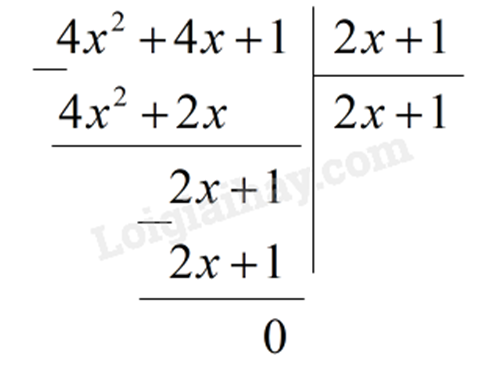
Vậy $A\left( x \right):\left( {2x + 1} \right) = 2x + 1$

a) Chứng minh $\Delta IMN = \Delta IKN$(cạnh huyền - góc nhọn)

b) Chứng minh $IM = IK$, IP > IK nên IP > IM.

c) Chứng minh I là trực tâm của tam giác QNP nên $ND \bot QP$.

Chứng minh $\Delta NQP$ cân tại $N$ nên DQ = DP.

$\Delta QIP$ có $ID$ vừa là đường cao, vừa là đường trung tuyến nên $\Delta QIP$ cân tại $I$

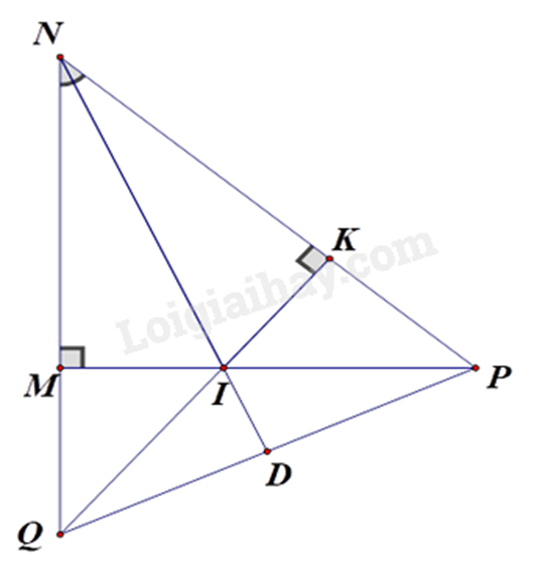
a) Xét $\Delta IMN$ và $\Delta IKN$ có:

$\widehat {IMN} = \widehat {IKN} = {90^0}$

NI chung

$\widehat {MNI} = \widehat {KNI}$ (NI là đường phân giác NI của góc MNP)

suy ra $\Delta IMN = \Delta IKN$(cạnh huyền - góc nhọn) (đpcm)

b) Vì $\Delta IMN = \Delta IKN$ nên IM = IK (hai cạnh tương ứng) (1)

Vì $\Delta IKP$ vuông tại K nên IP > IK (2)

Từ (1) và (2) suy ra IP > IM (đpcm)

c) Xét $\Delta NQP$ có đường cao QK và PM cắt nhau tại I nên I là trực tâm của tam giác NQP.

Do đó $ND \bot QP$ (đpcm)

Vì $\Delta NQP$ có ND vừa là đường cao vừa là đường phân giác nên $\Delta NQP$ cân tại N.

Suy ra ND là đường trung tuyến của tam giác NQP hay QD = DP.

Xét $\Delta QIP$ có ID vừa là đường cao vừa là đường trung tuyến nên $\Delta QIP$ cân tại I.

Phân tích đa thức A(x) để chứng minh A(x) > 0 với mọi x.

Do đó A(x) không có nghiệm.

Ta có:

$\begin{array}{l}A(x) = {x^2} + 2x + 2\\ = {x^2} + x + x + 1 + 1\\ = x(x + 1) + (x + 1) + 1\\ = (x + 1)(x + 1) + 1\end{array}$

$= {(x + 1)^2} + 1 > 0$ với mọi x.

Vậy đa thức A (x) = ${x^2} + 2x + 2$ không có nghiệm.