Đề thi học kì 2 Toán 7 - Đề số 12 - Chân trời sáng tạo — Không quảng cáo

Dựa vào kiến thức về tỉ lệ thức.

Ta có:

\(\frac{1}{2} = \frac{2}{4} \ne \frac{{ - 2}}{4}\) nên A sai.

\(\frac{1}{2} = \frac{5}{{10}}\) nên B đúng.

\(\frac{1}{2} = \frac{2}{4} \ne \frac{3}{4}\) nên C sai.

\(\frac{1}{2} = \frac{{ - 3}}{{ - 6}} \ne \frac{{ - 2}}{{ - 6}}\) nên D sai.

Đáp án B.

Dựa vào kiến thức về tỉ lệ thức: Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\).

Ta có: \(\frac{6}{x} = \frac{{ - 10}}{5}\) nên

\(\begin{array}{l}6.5 = \left( { - 10} \right).x\\x = \frac{{6.5}}{{ - 10}}\\x =  - 3\end{array}\)

Đáp án B.

Sử dụng kiến thức về hai đại lượng tỉ lệ thuận: Nếu đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ là a thì ta có công thức \(y = ax\)

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2 nên y = 2x.

Đáp án A.

Sử dụng công thức tính diện tích hình thang để viết biểu thức.

Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài) là: \(\frac{{\left( {a + b} \right).h}}{2}\).

Đáp án D.

Hệ số của hạng tử bậc 0 gọi là hệ số tự do của đa thức đó.

Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là – 22.

Đáp án A.

Thay \(x =  - 1\) vào đa thức để tính giá trị.

Thay \(x =  - 1\) vào đa thức g(x) ta được:

\(g\left( x \right) = {\left( { - 1} \right)^8}{\rm{ + }}{\left( { - 1} \right)^4} + {\left( { - 1} \right)^2} + 1 = 1 + 1 + 1 + 1 = 4\)

Đáp án D.

Dựa vào kiến thức về các loại biến cố.

Biến cố “Gieo hai con xúc xắc 1 lần, tổng số chấm xuất hiện trên hai con xúc xắc là 7” là biến cố ngẫu nhiên.

Đáp án D.

Dựa vào kiến thức về xác suất của các biến cố đồng khả năng.

Do đồng xu cân đối nên biến cố “Đồng xu xuất hiện mặt ngửa” và “Đồng xu xuất hiện mặt sấp” là đồng khả năng nên xác suất của 2 biến cố này bằng nhau và bằng \(\frac{1}{2}\).

Đáp án C.

Dựa vào mối quan hệ giữa góc và cạnh đối nhau trong một tam giác và định lí tổng ba góc của một tam giác bằng \({180^0}\).

Tam giác ABC vuông tại A có \(\widehat B = {65^0}\) nên

\(\widehat C = {180^0} - \widehat A - \widehat B = {180^0} - {90^0} - {65^0} = {25^0}\).

Vì \(\widehat A > \widehat B > \widehat C\left( {{{90}^0} > {{65}^0} > {{25}^0}} \right)\) nên \(BC > AC > AB\).

Đáp án B.

Dựa vào kiến thức về trọng tâm của tam giác.

Vì G là trọng tâm của tam giác ABC nên \(AG = \frac{2}{3}AM\) suy ra \(GM = AM - AG = AM - \frac{2}{3}AM = \frac{1}{3}AM\).

Suy ra \(\frac{{GM}}{{AG}} = \frac{{\frac{1}{3}AM}}{{\frac{2}{3}AM}} = \frac{1}{2}\) hay \(AG = 2GM\).

Đáp án B.

Dựa vào quan hệ giữa các cạnh của một tam giác.

Ta có:

4 + 5 = 9 < 10, ba độ dài \(4cm,\;5cm,\;10cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.

5 + 5 = 10 < 12, ba độ dài \(5cm,\;5cm,\;12cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.

11 > 20 – 11 = 9, ba độ dài \(11cm,\;11cm,\;20cm\) thỏa mãn điều kiện của bất đẳng thức tam giác nên đây có thể là độ dài ba cạnh của một tam giác.

11 = 20 – 9, ba độ dài \(9cm,\;20cm,\;11cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.

Đáp án C.

Dựa vào định lí tổng ba góc của một tam giác bằng \({180^0}\).

Số đo góc C là:

\(\begin{array}{l}\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {35^0} - {45^0}\\ = {100^0}\end{array}\)

Đáp án D.

a) Thay \(x = - 2,\;y = \frac{1}{3}\) vào A để tính giá trị biểu thức.

b) Sử dụng các phép tính với đa thức một biến để tìm giá trị của x.

a) Tại \(x = - 2,\;y = \frac{1}{3}\) ta có

\(\begin{array}{l}A = \left[ {2 \cdot ( - 2) + \frac{1}{3}} \right]\left[ {2 \cdot ( - 2) - \frac{1}{3}} \right]\\ = \left( { - 4 + \frac{1}{3}} \right)\left( { - 4 - \frac{1}{3}} \right)\\ = \frac{{ - 11}}{3}.\frac{{ - 13}}{3}\\ = \frac{{143}}{9}.\end{array}\)

b) \(x(3x - 2) - 3{x^2} = \frac{3}{4}\)

\(\begin{array}{l}3{x^2} - 2x - 3{x^2} = \frac{3}{4}\\ - 2x = \frac{3}{4}\\x = \frac{{ - 3}}{8}.\end{array}\)

Vậy \(x = \frac{{ - 3}}{8}\).

Gọi số tấm thiệp của ba lớp 7A, 7B, 7C lần lượt là \(x,y,z\left( {x,y,z \in {\mathbb{N}^ * }} \right)\)

Viết phương trình dựa vào đề bài.

Áp dụng tính chất dãy tỉ số bằng nhau để tìm x, y, z.

Gọi số tấm thiệp của ba lớp 7A, 7B, 7C lần lượt là \(x,y,z\left( {x,y,z \in {\mathbb{N}^ * }} \right)\)

Vì có 40 tấm thiệp nên x + y + z = 40

Vì số học sinh tỉ lệ với số thiệp cần làm nên ta có \(\frac{x}{{45}} = \frac{y}{{42}} = \frac{z}{{33}}\).

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{x}{{45}} = \frac{y}{{42}} = \frac{z}{{33}} = \frac{{x + y + z}}{{45 + 42 + 33}} = \frac{{40}}{{120}} = \frac{1}{3}\)

Từ đó ta tính được \(\left( {x,y,z} \right) = \left( {15;14;11} \right)\).

Vậy số tấm thiệp của ba lớp 7A, 7B, 7C lần lượt là 15; 14; 11.

Thực hiện tính toán với đa thức một biến.

a) \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\)

\(\begin{array}{l} = 5{x^4} + \left( { - 7{x^2} - 6{x^2}} \right) + \left( { - 3x + 11x} \right) - 30\\ = 5{x^4} - 13{x^2} + 8x - 30\end{array}\)

\(B\left( x \right) =  - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\)

\(\begin{array}{l} = 13{x^4} + \left( { - 11{x^3} + 20{x^3}} \right) + \left( {5x - 34x} \right) + \left( { - 10 - 2} \right)\\ = 13{x^4} + 9{x^3} - 29x - 12\end{array}\)

b) \(A\left( x \right) - B\left( x \right) = \left( {5{x^4} - 13{x^2} + 8x - 30} \right) - \left( {3{x^4} + 9{x^3} - 29x - 12} \right)\)

\(\begin{array}{l} = 5{x^4} - 13{x^2} + 8x - 30 - 3{x^4} - 9{x^3} + 29x + 12\\ = \left( {5{x^4} - 3{x^4}} \right) - 9{x^3} - 13{x^2} + \left( {8x + 29x} \right) + \left( { - 30 + 12} \right)\\ = 2{x^4} - 9{x^3} - 13{x^2} + 37x - 18\end{array}\)

a) Chứng minh \(\Delta ABH = \Delta ACK\) theo trường hợp cạnh huyền – góc nhọn. suy ra AH = AK nên tam giác AKH là tam giác cân.

b) Chứng minh \(\widehat {{P_1}} = \widehat {{N_1}}\) nên \(\Delta AKI = \Delta AHI\) theo trường hợp cạnh huyền – cạnh góc vuông suy ra \(\widehat {AIK} = \widehat {AIH}\)

Từ đó ta có \(\widehat {CIM} = \widehat {BIM}\) nên IM là phân giác của góc BIC

c) Từ tam giác cân ABC và AHK ta có \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\), \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) nên \(\widehat {ABC} = \widehat {AKH}\).

Mà hai góc này ở vị trí đồng vị nên HK // BC.

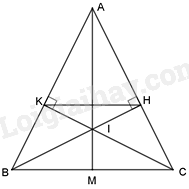
a) Xét \(\Delta ABH\) và \(\Delta ACK\) có:

\(\widehat {AHB} = \widehat {AKC} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\))

AB = AC (\(\Delta ABC\) cân);

góc A chung;

Do đó: \(\Delta ABH = \Delta ACK\) (cạnh huyền – góc nhọn).

\( \Rightarrow AH = AK \Rightarrow \Delta AHK\) cân tại A (đpcm).

b) Xét \(\Delta AKI\) và \(\Delta AHI\) có: \(\widehat {AKI} = \widehat {AHI} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\))

AK = AH (\(\Delta AHK\) cân tại A );

cạnh AI chung;

Do đó: \(\Delta AKI = \Delta AHI\) (cạnh huyền – cạnh góc vuông).

\( \Rightarrow \widehat {AIK} = \widehat {AIH}\).

Mà: \(\widehat {AIK} = \widehat {CIM};\widehat {AIH} = \widehat {BIM}\) (2 góc đối đỉnh).

Do đó: \(\widehat {CIM} = \widehat {BIM}\)\( \Rightarrow IM\)là phân giác của góc BIC (đpcm).

c) \(\Delta ABC\) cân tại A nên: \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\) .

\(\Delta AHK\) cân tại A nên: \(\widehat {AKH} = \frac{{180^\circ  - \widehat A}}{2}\) .

Suy ra \(\widehat {ABC} = \widehat {AKH}\).

Mà 2 góc này ở vị trí đồng vị.

Do đó: KH // BC (đpcm).

Biến đổi \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\) thành \(\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4}\).

Áp dụng tính chất dãy tỉ số bằng nhau để suy ra \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2} = 0\)

Từ đó ta có \(6z = 12x = 8y\).

Đặt \(6z = 12x = 8y = 24k\left( {k > 0} \right) \Rightarrow \left( {x;y;z} \right) = \left( {2k;3k;4k} \right)\)

Tìm k dựa vào \(200 < {y^2} + {z^2} < 450\)

Từ đó tính được x, y, z.

Ta có \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\) nên

\(\begin{array}{l}\frac{{3\left( {z - 4x} \right)}}{{3.3}} = \frac{{4\left( {3x - 2y} \right)}}{{4.4}} = \frac{{2\left( {4y - 3z} \right)}}{{2.2}}\\\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4}\end{array}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4} = \frac{{6z - 12x + 12x - 8y + 8y - 6z}}{{9 + 16 + 4}} = \frac{0}{{29}} = 0\)

Do đó \(\left\{ \begin{array}{l}6z - 12x = 0\\12x - 8y = 0\\8y - 6z = 0\end{array} \right.\) hay \(6z = 12x = 8y\).

Đặt \(6z = 12x = 8y = 24k\left( {k > 0} \right)\) ta được \(\left( {x;y;z} \right) = \left( {2k;3k;4k} \right)\)

Theo giả thiết \(200 < {y^2} + {z^2} < 450\) hay \(200 < 9{k^2} + 16{k^2} < 450\)

suy ra \(200 < 25{k^2} < 450 \Rightarrow k \in \left\{ {3;4} \right\}\)

Từ đó tìm được \(\left( {x;y;z} \right) \in \left\{ {\left( {6;9;12} \right);\left( {8;12;16} \right)} \right\}\)