Đề thi vào 10 môn Toán Bắc Giang 2023 có đáp án và lời giải chi tiết — Không quảng cáo

Đề bài

Phần I: Trắc nghiệm (3 điểm)

Câu 1: Đường thẳng $d:y = 4x + 1$ và parabol $\left( P \right):y = {x^2}$ có số điểm chung là

A. 0

B. 3

C. 1

D. 2

Câu 2: Phương trình ${x^2} + 3x - 4 = 0$ có hai nghiệm ${x_1},{x_1}$. Giá trị của biểu thức $A = {x_1} + {x_2}$ là:

A. 3

B. -4

C. -3

D. 4

Câu 3: Cho $\Delta ABC$ vuông tại $A$, có $AB = 24,AC = 18$ Chu vi đường tròn ngoại tiếp $\Delta ABC$ bằng

A. $30\pi$.

B. $225\pi$.

C. $60\pi$.

D. $15\pi$.

Câu 4: Cho $\Delta ABC$ vuông tại $A$ có $AB = 3\;{\rm{cm}}$ và $\angle B = 60^\circ$. Độ dài cạnh AC bằng:

A. $\sqrt 3 \;{\rm{cm}}$.

B. $6\sqrt 3 \;{\rm{cm}}$.

C. $2\sqrt 3 \;{\rm{cm}}$

D. $3\sqrt 3 \;{\rm{cm}}$.

Câu 5: Cho $\Delta ABC$ vuông tại $A$, có $AB = 12\;{\rm{cm}},AC = 16\;{\rm{cm}}$. Độ dài đường cao kẻ từ $A$ của $\Delta ABC$ là:

A. $9,6\;{\rm{cm}}$.

B. $4,8\;{\rm{cm}}$.

C. $15\;{\rm{cm}}$.

D. $10\;{\rm{cm}}$.

Câu 6: Cho đường tròn $\left( C \right)$ có tâm $O$ và bán kính $R = 10\;{\rm{cm}},AB$ là một dây cung của đường tròn $\left( C \right)$, gọi $H$ là trung điểm của AB. Biết $AB = 16\;{\rm{cm}}$, độ dài đoạn thẳng OH bằng

A. $5\;{\rm{cm}}$.

B. $8\;{\rm{cm}}$.

C. $6\;{\rm{cm}}$.

D. $3\;{\rm{cm}}$.

Câu 7: Một người thợ điện cần căng dây điện qua khu vực có một cây cau thẳng đứng. Để đảm bảo dây điện không vướng vào cây, người đó sử dụng thước ngắm có góc vuông đo chiều cao của cây như hình bên. Biết khoảng cách từ vị trí gốc cây đến vị trí chân của người thợ là $3,6\;{\rm{m}}$ và từ vị trí chân đứng thẳng trến mặt đất đến mắt của người ngắm là $1,6\;{\rm{m}}$. Với các kích thước trên, người thợ đo được khoảng cách từ điểm cao nhất của cây đến mặt đất theo phương vuông góc là (làm tròn đến chữ số hàng đơn vị)

A. $16\;{\rm{m}}$.

B. $10\;{\rm{m}}$.

C. $9\;{\rm{m}}$.

D. 4m.

Câu 8: Giá trị của biểu thức $\sqrt {3 - 2\sqrt 2 } {\rm{ \;}} + \sqrt {3 + 2\sqrt 2 }$ là

A. $2\sqrt 2$.

B. $2\sqrt 2 {\rm{ \;}} - 2$.

C. -2 .

D. 2 .

Câu 9: Với $x \ge 4$, kết quả rút gọn của biểu thức $\sqrt {25x - 100}$ là

A. $5\sqrt {x - 2}$.

B. $- 5\sqrt {x - 4}$.

C. $25\sqrt {x - 4}$.

D. $5\sqrt {x - 4}$.

Câu 10: Hàm số nào đưới đây đồng biến trến $R$ ?

A. $y = x + 1$.

B. $y = {x^2}$.

C. $y = {\rm{ \;}} - 2{x^2}$.

D. $y = {\rm{ \;}} - 3x + 2$.

Câu 11: Hàm số $y = {\rm{ \;}} - 5{x^2}$ nghịch biến khi

A. $x \in \mathbb{R}$.

B. $x > 0$.

C. $x = 0$.

D. $x < 0$.

Câu 12: Điều kiện của $x$ để biểu thức $A = \sqrt {x + 2}$ có nghĩa là

A. $x \le {\rm{ \;}} - 2$.

B. $x \ge {\rm{ \;}} - 2$.

C. $x \le 2$.

D. $x \ge 2$

Câu 13: Cho $x$ không âm và $\sqrt x {\rm{ \;}} = 3$, giá trị của $x$ là

A. 9 .

B. 18 .

C. 3.

D. 81

Câu 1 4 : $\left\{ {\begin{array}{*{20}{l}}{3x + ky = 6}\\{x + 2y = 2}\end{array}} \right.$ vô số nghiệm khi

A. $k = 3$.

B. $k = 1$.

C. $k = 6$.

D. $k = {\rm{ \;}} - 3$.

Câu 15: Hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{x + y = {\rm{ \;}} - 1}\\{2x - y = 4}\end{array}} \right.$ có nghiệm là $\left( {{x_0};{y_0}} \right)$. Giá trị của biểu thức $2{x_0} + {y_0}$ bằng

A. -1

B. -3

C. 0

D. 3

Câu 16: Cho đường trờn $\left( {O;3} \right)$ và điểm $M$ thỏa mãn $OM = 5$. Từ $M$ kẻ cát tuyến MAB với $\left( {O;3} \right)(A$ và $B$ là các giao điểm). Tích MA.MB bằng

A. 15.

B. 9.

C. 16

D. 15.

Câu 1 7 : Trong hệ tọa độ Oxy, đường thẳng $y = 2x + m$ đi qua điểm $M\left( {2; - 1} \right)$

A. $m = 4$.

B. $m = {\rm{ \;}} - 5$.

C. $m = 3$,

D. $m = 5$.

Câu 18: Cặp số $\left( {{x_0};{y_0}} \right)$ nào dưới đây là nghiệm của phương trình $2x - y = 2$ ?

A. $\left( { - 3;4} \right)$.

B. $\left( {3; - 4} \right)$.

C. $\left( {3;4} \right)$.

D. $\left( {4;3} \right)$.

Câu 19: Hàm số $y = \left( {2023 - m} \right)x + 2022$ nghịch biến trên $\mathbb{R}$ với giá trị của $m$ thỏa mãn

A. $m < 2023$.

B. $m > 2023$.

C. $m \ge 2023$.

D. $m \le 2023$.

Câu 20: Giá tiền điện hàng tháng ở nhà Việt được tính theo 4 mức như sau: mức 1: tính cho $100{\rm{KW}}$ đầu tiên; mức 2: tính cho số ${\rm{KW}}$ điện từ $101{\rm{KW}}$ đến $150{\rm{KW}}$, mỗi ${\rm{KW}}$ ở mức 2 đắt hơn 200 đồng so với mức 1 ; mức 3: tính cho số ${\rm{KW}}$ điện từ $151{\rm{KW}}$ đến $200{\rm{KW}}$, mỗi ${\rm{KW}}$ ở mức 3 đắt hon 200 đồng so với mức 2 ; mức 4 : từ ${\rm{KW}}$ thứ 201 tính chung 1 giá, mỗi ${\rm{KW}}$ ở mức 4 đắt hơn so với mức 3 là 100 đồng. Ngoài ra, người sử dụng còn phải trả thêm $10\%$ thuế giá trị gia tăng. Biết tháng vừa rồi nhà Việt dùng hết  điện

và phải trả 464200 đồng. Số tiền nhà Việt phải trả cho mỗi KW điện ở mức 1 là (kết quả làm tròn đến chữ số hàng đơn vị)

Phần II. Tự luận (7 điểm)

Câu 2 1 :

a) Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x - 2y = 9}\\{x - 3y = 10}\end{array}} \right.$

b) Rút gọn biều thức $Q = \left( {\frac{1}{{\sqrt x  - 1}} + \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x  + 1}} - \frac{2}{{1 - x}}} \right)$ với $x > 0$ và $x \ne 1$.

c) Biết đường thẳng $y = ax + b$ đi qua điểm $M\left( {2;1} \right)$ và song song với đường thẳng $y = x + 2023$. Tìm các hệ số $a$ và $b$.

Câu 22: Cho phương trình ${x^2} - 2\left( {m + 1} \right)x + 4m = 0$ (1), với $m$ là tham số.

a) Giải phương trình (1) khi $m = 2$.

b) Tìm $m$ để phương trình (1) có hai nghiệm phân biệt ${x_1},{x_2}$ thỏa mãn $\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 4$.

Câu 23: Trong dịp Tết trồng cây đầu năm, ban tổ chức dự kiến trồng 80 cây xanh. Tuy nhiên, đến ngày tổ chức có 4 người không thể tham gia trồng cây nên mỗi người còn lại phải trồng thêm 1 cây để hoàn thành công việc. Biết số cây mỗi người trồng được chia đều bằng nhau. Hỏi lúc đầu ban tổ chức dự kiến có bao nhiêu người tham gia trồng cây?

Câu 24: Cho $\Delta ABC$ có ba góc nhọn nội tiếp đường tròn $\left( {O;R} \right)$. Các đường cao $AD,BF,CE$ của $\Delta ABC$ cắt nhau tại $H$.

a) Chứng minh tứ giác $BEHD$ nội tiếp một đường tròn.

b) Kéo dài $AD$ cắt đường tròn $\left( O \right)$ tại điểm thứ hai $K$. Kéo dài $KE$ cắt đương tròn $\left( O \right)$ tại điểm thứ hai $I$. Gọi $N$ là giao điểm của $CI$ và $EF$. Chứng minh $C{E^2} = CN.CI$

c) Kẻ $OM$ vuông góc với $BC$ tại $M$. Gọi $P$ là tâm đường trờn ngoại tiếp $\Delta AEF$.

Chứng minh ba điểm $M,N,P$ thẳng hàng.

Câu 2 5 : Cho các số thực dương $a,b,c$ thỏa mãn điều kiện $a + b + c = 3$. Tìm giá trị lớn nhất của biểu thức $A = \sqrt {3a + bc}  + \sqrt {3b + ac}  + \sqrt {3c + ab}$.

-----HẾT-----

Lời giải chi tiết

Phần I: Trắc nghiệm

Câu 1 (TH):

Phương pháp:

Xét phương trình hoành độ giao điểm.

Giải phương trình bậc hai một ẩn.

Cách giải:

Xét phương trình hoành độ giao điểm của $d:y = 4x + 1$ và $\left( P \right):y = {x^2}$ ta được:

$\begin{array}{*{20}{l}}{{x^2} = 4x + 1}\\{ \Leftrightarrow {x^2} - 4x - 1 = 0}\\{ \Leftrightarrow ({x^2} - 4x + 4) - 5 = 0}\\{ \Leftrightarrow {{(x - 2)}^2} = 5}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 2 = \sqrt 5 }\\{x - 2 = {\rm{ \;}} - \sqrt 5 }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \sqrt 5 {\rm{ \;}} + 2}\\{x = {\rm{ \;}} - \sqrt 5 {\rm{ \;}} + 2}\end{array}} \right.}\end{array}$

Vậy đường thẳng và parabol có 2 điểm chung.

Chọn D.

Câu 2 (NB):

Phương pháp:

Hệ thức Vi-ét: $\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.$

Cách giải:

Phương trình ${x^2} + 3x - 4 = 0$

Suy ra $A = {x_1} + {x_2} = \frac{{ - 3}}{1} = {\rm{ \;}} - 3$

Chọn C.

Câu 3 (TH):

Phương pháp:

Đường tròn ngoại tiếp $\Delta ABC$ vuông tại $A$ với đường kính BC

Áp dụng định lí Pytago tính cạnh BC.

Chu vi đường tròn bằng $\pi .d$ với d là đường kính.

Cách giải:

Đường tròn ngoại tiếp $\Delta ABC$ vuông tại $A$ đường kính BC.

Áp dụng định lí Pytago $\Delta ABC$ vuông tại A có: $BC = \sqrt {A{B^2} + A{C^2}} {\rm{ \;}} = \sqrt {{{24}^2} + {{18}^2}} {\rm{ \;}} = 30$$\Rightarrow d = 30$

Chu vi đường tròn ngoại tiếp $\Delta ABC$ bằng $\pi .30 = 30\pi$

Chọn A.

Câu 4 (NB):

Phương pháp:

Sử dụng công thức $\tan B = \frac{{AC}}{{AB}}$

Cách giải:

Vì $\Delta ABC$ vuông tại $A$ $\Rightarrow \tan B = \frac{{AC}}{{AB}}$ $\Rightarrow AC = AB.\tan B = 3.\tan {60^^\circ }{\rm{ \;}} = 3\sqrt 3 (cm)$

Chọn D.

Câu 5 (NB):

Phương pháp:

Hệ thức lượng trong $\Delta ABC$ vuông tại $A$, đường cao AH: $\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$

Cách giải:

Hệ thức lượng trong $\Delta ABC$ vuông tại $A$, đường cao AH: $\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$

$\Rightarrow A{H^2} = \frac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2}}} \Rightarrow AH = \frac{{12.16}}{{\sqrt {{{12}^2} + {{16}^2}} }} = \frac{{48}}{5} = 9,6(cm)$

Chọn A.

Câu 6 (NB):

Phương pháp:

Đườn kính đi qua trung điêm của dây không đi qua tâm thì vuông góc với dây đó.

Áp dụng định lí Pytago để tính OH.

Cách giải:

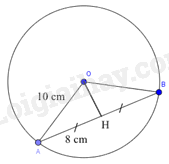
Xét (O) có H là trung điểm của AB $\Rightarrow OH \bot AB$

Áp dụng định lí Pytago vào $\Delta OAH$ vuông tại H có:

$OH = \sqrt {O{A^2} - A{H^2}} {\rm{ \;}} = \sqrt {{{10}^2} - {8^2}} {\rm{ \;}} = 6(cm)$

Chọn C.

Câu 7 (VD):

Phương pháp:

Dựng các điểm vào hình vẽ.

Áp dụng định lí Pytago để tính cạnh.

Chứng minh tam giác đồng dạng, suy ra cặp cạnh tương ứng tỉ lệ.

Cách giải:

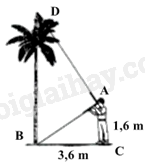
Áp dụng định lí Pytago vào $\Delta ABC$ vuông tại C có:$AB = \sqrt {B{C^2} + A{C^2}} {\rm{ \;}} = \sqrt {3,{6^2} + 1,{6^2}} {\rm{ \;}} = \frac{{2\sqrt {97} }}{5}(m)$

Xét $\Delta BCA$ và $\Delta DAB$ có:

$\angle BCA = \angle DAB = 90^\circ ;\angle ABC = \angle BDA$ (cùng phụ với $\angle ABD$)

$\Rightarrow \Delta BCA\backsim \Delta DAB(g-g)\Rightarrow \frac{BA}{DB}=\frac{CA}{AB}$ (cạnh tương ứng tỉ lệ)

$\Rightarrow DB = \frac{{A{B^2}}}{{AC}} = {\left( {\frac{{2\sqrt {97} }}{5}} \right)^2}:1,6 = 9,7 \approx 10$ (làm tròn đến hàng đơn vị)

Chọn B.

Câu 8 (NB):

Phương pháp:

Thực hiện tính toán đưa về dạng $\sqrt {{A^2}} {\rm{ \;}} = \left| A \right|$

Cách giải:

$\begin{array}{*{20}{l}}{\sqrt {3 - 2\sqrt 2 } {\rm{ \;}} + \sqrt {3 + 2\sqrt 2 } }\\{ = \sqrt {{{\left( {\sqrt 2 {\rm{ \;}} - 1} \right)}^2}} {\rm{ \;}} + \sqrt {{{\left( {\sqrt 2 {\rm{ \;}} + 1} \right)}^2}} }\\{ = \left| {\sqrt 2 {\rm{ \;}} - 1} \right| + \left| {\sqrt 2 {\rm{ \;}} + 1} \right|}\\{ = \sqrt 2 {\rm{ \;}} - 1 + \sqrt 2 {\rm{ \;}} + 1}\\{ = 2\sqrt 2 }\end{array}$

Chọn A.

Câu 9 (NB):

Phương pháp:

Đưa một số ra ngoài dấu căn $\sqrt {{A^2}.B} {\rm{ \;}} = \left| A \right|.B$

Cách giải:

Với $x \ge 4$, ta có $\sqrt {25x - 100} {\rm{ \;}} = \sqrt {25(x - 4)} {\rm{ \;}} = 5\sqrt {x - 4}$

Chọn D.

Câu 10 (NB):

Phương pháp:

Hàm số $y = ax + b(a \ne 0)$ đồng biến trên $R$ khi $a > 0$

Cách giải:

Hàm số $y = x + 1$ đồng biến trên $R$

Chọn A.

Câu 11 (NB):

Phương pháp:

Hàm số $y = a{x^2}(a \ne 0)$ nghịch biến trên $R$ khi $\left\{ {\begin{array}{*{20}{l}}{a > 0}\\{x < 0}\end{array}} \right.$ hoặc $\left\{ {\begin{array}{*{20}{l}}{a < 0}\\{x > 0}\end{array}} \right.$

Cách giải:

Hàm số $y = {\rm{ \;}} - 5{x^2}$ nghịch biến khi $\left\{ {\begin{array}{*{20}{l}}{ - 5 < 0}\\{x > 0}\end{array}} \right.$

Chọn B.

Câu 12 (NB):

Phương pháp:

Điều kiện xác định của $\sqrt {f(x)}$ là $f(x) \ge 0$

Cách giải:

$\sqrt {x + 2}$ có nghĩa khi $x + 2 \ge 0 \Leftrightarrow x \ge {\rm{ \;}} - 2$

Chọn B.

Câu 13 (NB):

Phương pháp:

Căn bậc hai số học của số x không âm là số a không âm sao cho ${a^2} = x$

Cách giải:

$\sqrt x {\rm{ \;}} = 3 \Leftrightarrow x = {3^2} = 9$

Chọn A.

Câu 14 (NB):

Phương pháp:

Hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{ax + by = c}\\{a'x + b'y = c'}\end{array}} \right.$ có vô số nghiệm khi $\frac{a}{{a'}} = \frac{b}{{b'}} = \frac{c}{{c'}}$

Cách giải:

Hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x + ky = 6}\\{x + 2y = 2}\end{array}} \right.$ vô số nghiệm khi: $\frac{3}{1} = \frac{k}{2} = \frac{6}{2} \Rightarrow k = 6$

Chọn C.

Câu 15 (TH):

Phương pháp:

Giải hệ phương trình bằng phương pháp cộng đại số.

Cách giải:

$\left\{ {\begin{array}{*{20}{l}}{x + y = {\rm{ \;}} - 1}\\{2x - y = 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x = 3}\\{y = {\rm{ \;}} - 1 - x}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = {\rm{ \;}} - 1 - 1 = {\rm{ \;}} - 2}\end{array}} \right.$

Hệ phương trình có nghiệm $\left( {{x_0};{y_0}} \right) = (1; - 2) \Rightarrow 2{x_0} + {y_0} = 2.1 + ( - 2) = 0$

Chọn C.

Câu 16 (VDC):

Phương pháp:

Dựng tiếp tuyến MC của (O) tại C.

Chứng minh $\Delta MAC\backsim \Delta MCB(g-g)$, sử dụng tính chất góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung.

Suy ra các cặp cạnh tương ứng tỉ lệ.

Cách giải:

Dựng tiếp tuyến MC của (O) tại C.

Áp dụng định lí Pytago vào $\Delta OMC$ vuông tại C có:

$M{C^2} = O{M^2} - O{C^2} = {5^2} - {3^2} = 16$

Xét $\Delta MAC$ và $\Delta MCB$ có:

$\angle BMC$ chung; $\angle ACM = \angle ABC$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cugn AC)

$\Rightarrow \Delta MAC\backsim \Delta MCB(g-g)\Rightarrow \frac{MA}{MC}=\frac{MC}{MB}$ (cạnh tương ứng tỉ lệ) $\Rightarrow MA.MB = M{C^2} = 16$

Chọn D.

Câu 17 (NB):

Phương pháp:

Thay tọa độ điểm vào đường thẳng.

Cách giải:

Thay tọa độ điểm $M\left( {2; - 1} \right)$ vào đường thẳng $y = 2x + m$ ta được: $- 1 = 2.2 + m \Leftrightarrow m = {\rm{ \;}} - 5$

Chọn B.

Câu 18 (NB):

Phương pháp:

Nghiệm của phương trình  $ax + by = c$ là $\left( {{x_0};{y_0}} \right)$ thỏa mãn $a{x_0} + b{y_0} = c$

Cách giải:

Xét $2x - y = 2$: với $x = 3 \Rightarrow y = 2.3 - 2 = 4$

Vậy $2x - y = 2$ có nghiệm $\left( {{x_0};{y_0}} \right) = \left( {3;4} \right)$

Chọn C.

Câu 19 (NB):

Phương pháp:

Hàm số $y = ax + b(a \ne 0)$ nghịch biến trên $R$ khi $a < 0$

Cách giải:

Hàm số $y = \left( {2023 - m} \right)x + 2022$ nghịch biến trên $\mathbb{R}$ khi: $2023 - m < 0 \Leftrightarrow m > 2023$

Chọn B.

Câu 20 (VD):

Phương pháp:

Giải bài toán bằng cách lập phương trình.

Cách giải:

Gọi số tiền điện nhà Việt phải trả theo mức 1 là $x$ (đồng).

Điều kiện: x > 0

Số tiền điện ở mức 2 là $x + 200$ (đồng)

Số tiền điện ở mức 3 là $x + 200 + 200 = x + 400$ (đồng)

Số tiền điện ở mức 4 là $x + 400 + 100 = x + 500$ (đồng)

Tổng tiền điện nhà Việt phải trả trước thuế là: $\frac{{464200}}{{1 + 10\% }} = 422000$ (đồng)

Lượng điện mà nhà Việt phải trả tiền ở mức 4 là: $205 - 100 - 50 - 50 = 5({\rm{KW}})$

Vì nhà Việt phải trả 422000 đồng trước thuế cho $100{\rm{KW}}$ điện ở mức 1;$50{\rm{KW}}$ ở mức 2 và 3 và $5{\rm{KW}}$ ở mức 4 nên ta có phương trình:

$\begin{array}{*{20}{l}}{100x + 50(x + 200) + 50(x + 400) + 5(x + 500) = 422000}\\{ \Leftrightarrow 100x + 50x + 10000 + 50x + 20000 + 5x + 2500 = 422000}\\{ \Leftrightarrow 205x + 32500 = 422000}\\{ \Leftrightarrow 205x = 389500}\\{ \Leftrightarrow x = 1900(tm)}\end{array}$

Vậy số tiền nhà Việt phải trả cho mỗi kWh điện ở mức 1 là 1900 đồng

Chọn D.

Phần II: Tự luận

Câu 21 (TH):

Phương pháp:

a) Giải hệ phương trình bằng phương pháp cộng đại số

b) Rút gọn biểu thức chưa căn bậc hai (Quy đồng, tính toán, thu gọn cẩn thận)

c) Hai đường thẳng $y = ax + b$ và $y = a'x + b'$ song song khi: $a = a';b \ne b'$

Thay điểm $M\left( {2;1} \right)$ vào $y = ax + b$

Giải hệ tìm hệ số $a$ và $b$.

Cách giải:

a) $\left\{ {\begin{array}{*{20}{l}}{3x - 2y = 9}\\{x - 3y = 10}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x - 2y = 9}\\{3x - 9y = 30}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x - 2y = 9}\\{7y = {\rm{ \;}} - 21}\end{array}} \right.$ $\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x - 2y = 9}\\{y = {\rm{ \;}} - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{{9 + 2.( - 3)}}{3}}\\{y = {\rm{ \;}} - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = {\rm{ \;}} - 3}\end{array}} \right.$

Vậy nghiệm của hệ phương trình là $\left( {x;y} \right) = \left( {1; - 3} \right)$.

b) Với $x > 0{\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} x \ne 1$ ta có:

$\begin{array}{l}Q = \left( {\frac{1}{{\sqrt x  - 1}} + \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x  + 1}} - \frac{2}{{1 - x}}} \right)\\\,\,\,\, = \left( {\frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x  - 1} \right)}} + \frac{1}{{\sqrt x \left( {\sqrt x  - 1} \right)}}} \right):\left( {\frac{{\sqrt x  - 1}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} + \frac{2}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}} \right)\\\,\,\,\, = \frac{{\sqrt x  + 1}}{{\sqrt x \left( {\sqrt x  - 1} \right)}}:\frac{{\sqrt x  - 1 + 2}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\\\,\,\,\, = \frac{{\sqrt x  + 1}}{{\sqrt x \left( {\sqrt x  - 1} \right)}}.\frac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}{{\sqrt x  + 1}}\\\,\,\,\, = \frac{{\sqrt x  + 1}}{{\sqrt x }}\end{array}$

Vậy với $x > 0{\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} x \ne 1$ thì $Q = \frac{{\sqrt x {\rm{ \;}} + 1}}{{\sqrt x }}$.

c) Vì đường thẳng y = ax + b song song với đường thẳng y = x + 2023 $\Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b \ne 2023}\end{array}} \right.$

Khi đó đường thẳng cần tìm là y = x + b với $b \ne 2023$

Vì đường thẳng y = x + b đi qua điểm $M\left( {2;1} \right)$ nên ta có phương trình: $1 = 2 + b \Leftrightarrow b = {\rm{ \;}} - 1{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)$

Vậy hệ số a = 1 và hệ số b = -1.

Câu 22 (VD):

Phương pháp:

a) Giải phương trình bậc hai một ẩn bằng công thức nghiệm $\Delta ' = {(b')^2} - ac$ với $b' = \frac{b}{2}$

Khi đó phương trình có nghiệm $\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a}}\\{{x_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a}}\end{array}} \right.$

b) Tìm nghiệm của phương trình theo m.

Sau đó thay vào biểu thức (2 trường hợp vì vai trò của ${x_1},{x_2}$ là như nhau)

Cách giải:

a) Với $m = 2$, phương trình (1) trở thành: ${x^2} - 6x + 8 = 0$

Ta có: $\Delta ' = {3^2} - 1.8 = 9 - 8 = 1 > 0$

Suy ra phương trình có nghiệm phân biệt là: ${x_1} = \frac{{3 + \sqrt 1 }}{1} = 3 + 1 = 4;{x_1} = \frac{{3 - \sqrt 1 }}{1} = 3 - 1 = 2$

Vậy với $m = 2$, phương trình có tập nghiệm là $S = \left\{ {4;2} \right\}$.

b) Xét phương trình ${x^2} - 2(m + 1)x + 4m = 0$ (1)

Ta có ${x^2} - 2(m + 1)x + 4m = 0$

$\begin{array}{*{20}{l}}{ \Leftrightarrow {x^2} - 2mx - 2x + 4m = 0}\\{ \Leftrightarrow x\left( {x - 2m} \right) - 2\left( {x - 2m} \right) = 0}\\{ \Leftrightarrow \left( {x - 2m} \right)\left( {x - 2} \right) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2m}\\{x = 2}\end{array}} \right.}\end{array}$

Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi $2m \ne 2 \Leftrightarrow m \ne 1$

Khi đó phương trình có 2 nghiệm phân biệt ${x_1},{x_2}$

TH1: $\left\{ {\begin{array}{*{20}{l}}{{x_1} = 2m}\\{{x_2} = 2}\end{array}} \right.$. Theo đề bài ta có: $\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 4 \Leftrightarrow \left| {2m} \right| - \left| 2 \right| = {\rm{ \;}} - 4 \Leftrightarrow \left| {2m} \right| = {\rm{ \;}} - 2$ (vô lý)

TH2:  $\left\{ {\begin{array}{*{20}{l}}{{x_1} = 2}\\{{x_2} = 2m}\end{array}} \right.$. Theo đề bài ta có: $\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 4 \Leftrightarrow \left| 2 \right| - \left| {2m} \right| = {\rm{ \;}} - 4 \Leftrightarrow \left| {2m} \right| = 6 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 3}\\{m = {\rm{ \;}} - 3}\end{array}} \right.$ (thỏa mãn)

Vậy $\left[ {\begin{array}{*{20}{l}}{m = 3}\\{m = {\rm{ \;}} - 3}\end{array}} \right.$ thì phương trình (1) có hai nghiệm phân biệt ${x_1},{x_2}$ thỏa mãn $\left| {{x_1}} \right| - \left| {{x_2}} \right| = {\rm{ \;}} - 4$

Câu 23 (TH):

Phương pháp:

Giải bài toán bằng cách lập phương trình, dạng toán kế hoạch - thực tế.

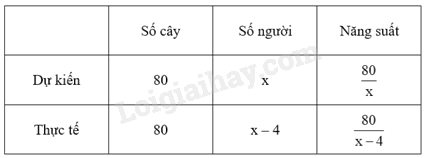
Thực tế mỗi người trồng nhiều hơn dự kiến 1 cây.

Cách giải:

Gọi x (người) là số người ban tổ chức dự kiến trồng cây ($x > 4,x \in \mathbb{N}$).

Số cây mỗi người phải trồng theo dự kiến là $\frac{{80}}{x}$ cây.

Số người trồng cây thực tế là: $x - 4$ (người)

Số cây mỗi người phải trồng theo thực tế là: $\frac{{80}}{{x - 4}}$ (cây).

Vì theo thực tế mỗi người còn lại phải trồng thêm 1 cây so với dự kiến để hoàn thành công việc nên ta có:

$\begin{array}{*{20}{l}}{\frac{{80}}{{x - 4}} - \frac{{80}}{x} = 1}\\{ \Leftrightarrow \frac{{80x}}{{x\left( {x - 4} \right)}} - \frac{{80\left( {x - 4} \right)}}{{x\left( {x - 4} \right)}} = 1}\\{ \Leftrightarrow \frac{{80x - 80\left( {x - 4} \right)}}{{x\left( {x - 4} \right)}} = 1}\\{ \Leftrightarrow \frac{{80x - 80x + 320}}{{x\left( {x - 4} \right)}} = 1}\\{ \Leftrightarrow \frac{{320}}{{x\left( {x - 4} \right)}} = 1}\end{array}$

$\begin{array}{l} \Leftrightarrow 320 = x\left( {x - 4} \right)\\ \Leftrightarrow {x^2} - 4x - 320 = 0\\ \Leftrightarrow {x^2} - 20x + 16x - 320 = 0\\ \Leftrightarrow x\left( {x - 20} \right) + 16\left( {x - 20} \right) = 0\\ \Leftrightarrow \left( {x - 20} \right)\left( {x + 16} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 20 = 0\\x + 16 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 20\,\,\left( {tm} \right)\\x =  - 16\,\,\left( {ktm} \right)\end{array} \right.\end{array}$

Vậy lúc đầu ban tổ chức dự kiến có 20 người tham gia trồng cây.

Câu 2 4: (VD) Cho $\Delta ABC$ có ba góc nhọn nội tiếp đường tròn $\left( {O;R} \right)$. Các đường cao $AD,BF,CE$ của $\Delta ABC$ cắt nhau tại $H$.

a) Chứng minh tứ giác $BEHD$ nội tiếp một đường tròn.

b) Kéo dài $AD$ cắt đường tròn $\left( O \right)$ tại điểm thứ hai $K$. Kéo dài $KE$ cắt đương tròn $\left( O \right)$ tại điểm thứ hai $I$. Gọi $N$ là giao điểm của $CI$ và $EF$. Chứng minh $C{E^2} = CN.CI$

c) Kẻ $OM$ vuông góc với $BC$ tại $M$. Gọi $P$ là tâm đường trờn ngoại tiếp $\Delta AEF$.

Chứng minh ba điểm $M,N,P$ thẳng hàng.

Phương pháp:

a) Chứng minh BEHD có tổng hai góc đối bằng $180^\circ$ là tứ giác nội tiếp.

b) Chứng minh AEHF có tổng hai góc đối bằng $180^\circ$ là tứ giác nội tiếp.

Suy ra hai góc nội tiếp cùng chắn cung HF bằng nhau

Chứng minh $\Delta CEN\backsim \Delta CIE\left( g.g \right)$ suy ra các cạnh tương ứng tỉ lệ.

c) Chứng minh MP là trung trực của EF, N là trung điểm của EF

Cách giải:

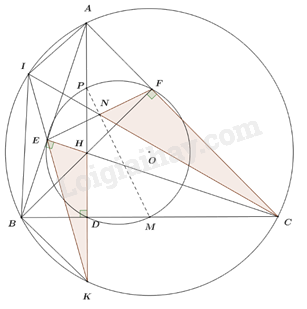
a) Do CE, AD, BF là các đường cao

$\Rightarrow \angle BEH = \angle BDH = \angle AFB = {90^0}$

$\Rightarrow \angle BEH + \angle BDH = {90^0} + {90^0} = {180^0}$

Mà 2 góc này ở vị trí đối diện nên tứ giác BEHD nội tiếp (đpcm)

b) Xét tứ giác AFHE có

$\angle BEH + \angle AFH = {90^0} + {90^0} = {180^0}$

Mà 2 góc này ở vị trí đối diện nên tứ giác AFHE nội tiếp (dhnb)

$\Rightarrow \angle HEF = HAF$ (góc nội tiếp cùng chắn cung HF)

Mà $\angle HAF = \angle KIC$ (góc nội tiếp cùng chắn cung KC)

$\Rightarrow \angle HEF = \angle KIC\left( { = HAF} \right)$ hay $\angle CEN = \angle EIC$

Xét $\Delta CNE$ và $\Delta CEI$ có: $\angle ECI$ chung và $\angle CEN = \angle EIC{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)$

$\Rightarrow \Delta CEN\backsim \Delta CIE\left( g.g \right)\Rightarrow \frac{CE}{CI}=\frac{CN}{CE}$ (cặp cạnh tương ứng tỉ lệ).

$\Leftrightarrow C{E^2} = CI.CN$ (đpcm)

c) Ta có: PE = PF (do P là tâm đường tròn ngoại tiếp tam giác AEF)

$\Rightarrow$ P thuộc trung trực của EF.

$\Delta BEC$ vuông tại E có M là trung điểm của BC

$\Rightarrow ME = MB = MC$ (trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)

$\Delta BFC$vuông tại F có M là trung điểm của BC

$\Rightarrow MF = MB = MC$ (trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).

=> $ME = MF = MB = MC$.

$\Rightarrow M$ thuộc trung trực của EF.

=> PM là trung trực của EF (*)

Ta cần chứng minh N thuộc trung trực của EF.

Theo ý b) ta có: $\Delta CNE\backsim \Delta CEI$ $\Rightarrow \frac{{NE}}{{IE}} = \frac{{NC}}{{CE}} \Rightarrow NE = \frac{{IE.NC}}{{CE}}$.

Xét tứ giác AEHF có: $\angle AEH + \angle AFH = {90^0} + {90^0} = {180^0}$

$\Rightarrow AEHF$ là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng ${180^0}$).

$\Rightarrow \angle AHE = \angle AFE$ (hai góc nội tiếp cùng chắn cung AE)

$\Rightarrow {180^0} - \angle AHE = {180^0} - \angle AFE \Rightarrow \angle KHE = \angle CFN$.

Xét $\Delta CFN$ và $\Delta KHE$ có:

$\angle CFN = \angle KHE{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)$

$\angle FCN = \angle HKE$ (hai góc nội tiếp cùng chắn cung AI).

$\Rightarrow \Delta CFN\backsim \Delta KHE\left( g.g \right)$

$\Rightarrow \frac{{FN}}{{HE}} = \frac{{CN}}{{KE}} \Rightarrow FN = \frac{{HE.CN}}{{KE}}$ (cặp cạnh tương ứng tỉ lệ).

Khi đó ta có: $\frac{{NE}}{{FN}} = \frac{{IE.NC}}{{CE}}:\frac{{HE.CN}}{{KE}} = \frac{{IE.NC.KE}}{{CE.HE.CN}} = \frac{{IE.KE}}{{CE.HE}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)$.

+) Xét $\Delta IEA$ và $\Delta BEK$ có:

$\angle IEA = \angle BEK$ (đối đỉnh)

$\angle IAE = \angle BKE$ (hai góc nội tiếp cùng chắn cung BI)

$\begin{array}{*{35}{l}}   \Rightarrow \Delta IEA\backsim \Delta BEK\left( g.g \right)  \\   \Rightarrow \frac{IE}{BE}=\frac{EA}{EK}\Rightarrow IE.EK=EA.BE\left( 2 \right) \end{array}$

+) Xét $\Delta AEH$ và $\Delta CEB$ có:

$\angle EAH = \angle ECB$ (cùng phụ với $\angle ABC$)

$\angle AEH = \angle CEB = {90^0}$ (hai góc nội tiếp cùng chắn cung BI)

$\begin{array}{*{35}{l}}  \Rightarrow \Delta AEH\backsim \Delta CEB\left( g.g \right)  \\   \Rightarrow \frac{AE}{EC}=\frac{EH}{EB}\Rightarrow EC.EH=EA.EB\left( 3 \right) \end{array}$

Thay (2), (3) vào (1) ta có: $\frac{{NE}}{{FN}} = \frac{{IE.KE}}{{CE.HE}} = \frac{{EA.BE}}{{EA.EB}} = 1 \Rightarrow NE = FN$.

$\Rightarrow N$ thuộc trung trực của EF (**)

Từ (*) và (**) => M, N, P thẳng hàng (đpcm).

Câu 25 (VDC):

Phương pháp:

Thay $a + b + c = 3$ vào biểu thức, biến đổi về dạng: $A = \sqrt {(a + b).(a + c)} {\rm{ \;}} + \sqrt {(a + b).(b + c)} {\rm{ \;}} + \sqrt {(a + c).(b + c)}$

Sau đó áp dụng BĐT Cosi cho các số dương.

Cách giải:

Ta có:

$A = \sqrt {3a + bc}  + \sqrt {3b + ac}  + \sqrt {3c + ab}$

$\begin{array}{l}A = \sqrt {\left( {a + b + c} \right)a + bc}  + \sqrt {\left( {a + b + c} \right)b + ac}  + \sqrt {\left( {a + b + c} \right)c + ab} \\A = \sqrt {\left( {{a^2} + ab} \right) + \left( {ac + bc} \right)}  + \sqrt {\left( {{b^2} + ab} \right) + \left( {bc + ac} \right)}  + \sqrt {\left( {{c^2} + bc} \right) + \left( {ac + ab} \right)} \\A = \sqrt {a\left( {a + b} \right) + c\left( {a + b} \right)}  + \sqrt {b\left( {a + b} \right) + c\left( {a + b} \right)}  + \sqrt {c\left( {b + c} \right) + a\left( {b + c} \right)} \\A = \sqrt {(a + b).(a + c)}  + \sqrt {(a + b).(b + c)}  + \sqrt {(a + c).(b + c)} \end{array}$

Áp dụng bất đẳng thức Côsi ta có:

$\begin{array}{*{20}{l}}{\sqrt {(a + b).(a + c)} {\rm{ \;}} \le \frac{{(a + b) + (a + c)}}{2}}\\{\sqrt {(a + b).(b + c)} {\rm{ \;}} \le \frac{{(a + b) + (b + c)}}{2}}\\{\sqrt {(a + c).(b + c)} {\rm{ \;}} \le \frac{{(a + c) + (b + c)}}{2}}\end{array}$

$\begin{array}{*{20}{l}}{ \Rightarrow \sqrt {(a + b).(a + c)} {\rm{ \;}} + \sqrt {(a + b).(b + c)} {\rm{ \;}} + \sqrt {(a + c).(b + c)} }\\{ \le \frac{{(a + b) + (a + c)}}{2} + \frac{{(a + b) + (b + c)}}{2} + \frac{{(a + c) + (b + c)}}{2}}\\{ \Rightarrow A \le \frac{{4a + 4b + 4c}}{2} = \frac{{4\left( {a + b + c} \right)}}{2} = \frac{{4.3}}{2} = 6}\end{array}$

Dấu “=” xảy ra $\Leftrightarrow$ $a = b = c = 1$.

Vậy giá trị lớn nhất của A bằng 6 khi $a = b = c = 1$.