Đề thi vào 10 môn Toán Bắc Ninh năm 2018 — Không quảng cáo

Đề bài

I. TRẮC NGHIỆM (3 điểm)

Chọn phương án trả lời đúng trong các câu sau:

Câu 1 Phương trình \({x^2} - 3x - 6 = 0\) có hai nghiệm \({x_1},\;\;{x_2}.\) Tổng \({x_1} + {x_2}\) bằng:

A. 3 B. -3 C. 6 D. -6

Câu 2 Đường thẳng \(y = x + m - 2\) đi qua điểm \(E\left( {1;\;0} \right)\) khi:

A. \(m =  - 1\) B. \(m = 3\) C. \(m = 0\) D. \(m = 1\)

Câu 3 Cho tam giác \(ABC\) vuông tại \(A,\;\;\widehat {ACB} = {30^0},\;\;AB = 5cm.\) Độ dài cạnh \(AC\) là:

A. \(10cm\) B. \(\dfrac{{5\sqrt 3 }}{2}cm\) C. \(5\sqrt 3 cm\) D. \(\dfrac{5}{{\sqrt 3 }}cm\)

Câu 4 Hình vuông cạnh bằng 1, bán kính đường tròn ngoại tiếp hình vuông là:

A. \(\dfrac{1}{2}\) B. \(1\) C. \(\sqrt 2 \) D. \(\dfrac{{\sqrt 2 }}{2}\)

Câu 5 Phương trình \({x^2} + x + a = 0\) (với x là ẩn, a là tham số) có nghiệm kép khi:

A. \(a =  - \dfrac{1}{4}\) B. \(a = \dfrac{1}{4}\) C. \(a = 4\) D. \( - 4\)

Câu 6 Cho \(a > 0,\) rút gọn biểu thức \(\dfrac{{\sqrt {{a^3}} }}{{\sqrt a }}\) ta được kết quả:

A.\({a^2}\) B. \(a\) C. \( \pm a\) D. \( - a\)

PHẦN II. TỰ LUẬN (7 điểm)

Câu 7 (2,5 điểm)

a) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 5\\3x - y = 1\end{array} \right..\)

b) Tìm tọa độ giao điểm \(A,\;B\) của đồ thị hàm số \(y = {x^2}\) và \(y = x + 2.\) Gọi \(D,\;C\) lần lượt là hình chiếu vuông góc của \(A,\;B\) lên trục hoành. Tính diện tích tứ giác \(ABCD.\)

Câu 8 (1 điểm)

Nhân dịp Tết Thiếu nhi 01/06, một nhóm học sinh cần chia đều một số lượng quyển vở thành các phần quà để tặng cho các em nhỏ tại một mái ấm tình thương. Nếu mỗi phần quà giảm 2 quyển thì các em sẽ có thêm 2 phần quà nữa, còn nếu mỗi phần quà giảm 4 quyển thì các em sẽ có thêm 5 phần quà nữa. Hỏi ban đầu có bao nhiêu phần quà và mỗi phần quà có bao nhiêu quyển vở?

Câu 9 (2,5 điểm)

Cho đường tròn đường kính AB, các điểm C, D nằm trên đường tròn đó sao cho C, D nằm khác phía đối với đường thẳng AB, đồng thời AD > AC. Gọi điểm chính giữa của các cung nhỏ AC và AD lần lượt là M, N; giao điểm của MN với AC, AD lần lượt là H, I; giao điểm của MD và CN là K.

a) Chứng minh \(\widehat {ACN} = \widehat {DMN}\). Từ đó suy ra tứ giác MCKH nội tiếp.

b) Chứng minh KH song song với AD.

c) Tìm hệ thức liên hệ giữa  và  để AK song song với ND.

Câu 10 (1 điểm)

a) Cho các số thực dương a, b, c thỏa mãn điều kiện \(a + b + c = 3\). Tìm giá trị nhỏ nhất của biểu thức \(A = 4{a^2} + 6{b^2} + 3{c^2}\)

b) Tìm các số nguyên dương a, b biết các phương trình \({x^2} - 2ax - 3b = 0\) và \({x^2} - 2bx - 3a = 0\) (với x là ẩn) đều có nghiệm nguyên.

Lời giải chi tiết

1	2	3	4	5	6
A	D	C	D	B	B

Câu 1:

Phương pháp:

Áp dụng hệ thức Vi-ét cho phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm \({x_1},\;{x_2}\) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right..\)

Cách giải:

Phương trình \({x^2} - 3x - 6 = 0\) có hai nghiệm \({x_1},\;\;{x_2}.\) Tổng \({x_1} + {x_2}\) bằng:

A. 3 B. -3 C. 6 D. -6

Ta có: \(a = 1;\;b =  - 3;\;c =  - 6.\)

Áp dụng hệ thức Vi-ét ta có: \({x_1} + {x_2} =  - \frac{b}{a} = 3.\)

Chọn A.

Câu 2:

Phương pháp:

Thay tọa độ điểm E vào công thức hàm số để tìm m.

Cách giải:

Đường thẳng \(y = x + m - 2\) đi qua điểm \(E\left( {1;\;0} \right)\) khi:

A. \(m =  - 1\) B. \(m = 3\) C. \(m = 0\) D. \(m = 1\)

Điểm \(E\left( {1;\;\;0} \right)\) thuộc đồ thị hàm số \(y = x + m - 2\) nên ta có:

\(0 = 1 + m - 2 \Leftrightarrow m = 1.\)

Chọn D.

Câu 3:

Phương pháp:

Xét tam giác ABC vuông tại A. Khi đó ta có: \(\tan C = \frac{{AB}}{{AC}} \Rightarrow AC = \frac{{AB}}{{\tan C}}.\)

Cách giải:

Cho tam giác \(ABC\) vuông tại \(A,\;\;\widehat {ACB} = {30^0},\;\;AB = 5cm.\) Độ dài cạnh \(AC\) là:

A. \(10cm\) B. \(\frac{{5\sqrt 3 }}{2}cm\) C. \(5\sqrt 3 cm\) D. \(\frac{5}{{\sqrt 3 }}cm\)

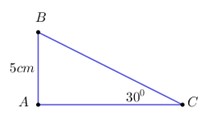
Ta có: \(\tan C = \frac{{AB}}{{AC}} \Rightarrow AC = \frac{{AB}}{{\tan C}} = \frac{5}{{\tan {{30}^0}}} = 5:\frac{1}{{\sqrt 3 }} = 5\sqrt 3 cm.\)

Chọn C.

Câu 4:

Phương pháp:

Tâm đường tròn ngoại tiếp hình vuông là giao điểm của hai đường chéo.

Sử dụng định lý Pi-ta-go để tính bán kính đường tròn ngoại tiếp hình vuông.

Cách giải:

Hình vuông cạnh bằng 1, bán kính đường tròn ngoại tiếp hình vuông là:

A. \(\frac{1}{2}\) B. \(1\) C. \(\sqrt 2 \) D. \(\frac{{\sqrt 2 }}{2}\)

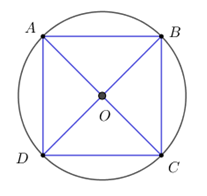
Xét hình vuông ABCD có các cạnh là 1.

Tâm đường tròn ngoại tiếp hình vuông ABCD là giao điểm O của hai đường chéo AC và BD.

Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại B ta có:

\(A{C^2} = A{B^2} + B{C^2} = 1 + 1 = 2 \Rightarrow AC = \sqrt 2 .\)

Có O là trung điểm của AC nên: \(OA = OC = R = \frac{{AC}}{2} = \frac{{\sqrt 2 }}{2}.\)

Chọn D.

Câu 5:

Phương pháp:

Phương trình bậc hai một ẩn có nghiệm kép \( \Leftrightarrow \Delta  = 0.\)

Cách giải:

Phương trình \({x^2} + x + a = 0\) (với x là ẩn, a là tham số) có nghiệm kép khi:

A. \(a =  - \frac{1}{4}\) B. \(a = \frac{1}{4}\) C. \(a = 4\) D. \( - 4\)

Phương trình đã cho có nghiệm kép \( \Leftrightarrow \Delta  = 0 \Leftrightarrow 1 - 4a = 0 \Leftrightarrow a = \frac{1}{4}.\)

Chọn B.

Câu 6:

Phương pháp:

Áp dụng công thức: \(\frac{{\sqrt A }}{{\sqrt B }} = \sqrt {\frac{A}{B}} ;\;\;\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\;\;khi\;\;A \ge 0\\ - A\;\;khi\;\;A < 0\end{array} \right..\)

Cách giải:

Cho \(a > 0,\) rút gọn biểu thức \(\frac{{\sqrt {{a^3}} }}{{\sqrt a }}\) ta được kết quả:

A.\({a^2}\) B. \(a\) C. \( \pm a\) D. \( - a\)

Ta có: \(\frac{{\sqrt {{a^3}} }}{{\sqrt a }} = \sqrt {\frac{{{a^3}}}{a}}  = \sqrt {{a^2}}  = \left| a \right| = a\;\;\left( {do\;\;a > 0} \right).\)

Chọn B.

PHẦN II. TỰ LUẬN (7 điểm)

Câu 7 (VD) (2,5 điểm)

a) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 5\\3x - y = 1\end{array} \right..\)

b) Tìm tọa độ giao điểm \(A,\;B\) của đồ thị hàm số \(y = {x^2}\) và \(y = x + 2.\) Gọi \(D,\;C\) lần lượt là hình chiếu vuông góc của \(A,\;B\) lên trục hoành. Tính diện tích tứ giác \(ABCD.\)

Câu 7:

Phương pháp:

+) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.

+) Lập phương trình hoành độ giao điểm của hai đồ thị để tìm tọa độ hai giao điểm \(A,\;B.\)

+) Vẽ đồ thị hai hàm số trên cùng hệ trục tọa độ.

+) Dựa vào hình vẽ để tính diện tích tứ giác ABCD.

Cách giải:

a) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 5\\3x - y = 1\end{array} \right..\)

\(\left\{ \begin{array}{l}x + 2y = 5\\3x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y = 5\\6x - 2y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 7\\y = 3x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right..\)

Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\;y} \right) = \left( {1;\;2} \right).\)

b) Tìm tọa độ giao điểm \(A,\;B\) của đồ thị hàm số \(y = {x^2}\) và \(y = x + 2.\) Gọi \(D,\;C\) lần lượt là hình chiếu vuông góc của \(A,\;B\) lên trục hoành. Tính diện tích tứ giác \(ABCD.\)

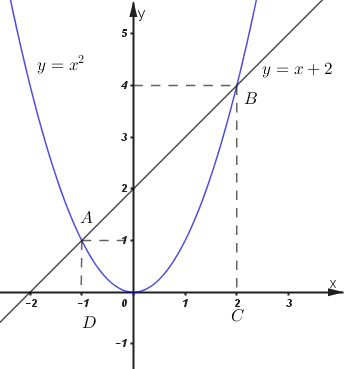
Phương trình hoành độ giao điểm của hai đồ thị hàm số là: \({x^2} = x + 2\)

\(\begin{array}{l} \Leftrightarrow {x^2} - x - 2 = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 1 \Rightarrow A\left( { - 1;\;1} \right)\\x = 2 \Rightarrow B\left( {2;\;4} \right)\end{array} \right..\end{array}\)

C là hình chiếu của B trên trục hoành \( \Rightarrow C\left( {2;\;0} \right).\)

D là hình chiếu của A trên trục hoành \( \Rightarrow D\left( { - 1;\;0} \right).\)

Dựa vào đồ thị hàm số ta thấy ABCD là hình thang vuông tại D và C.

\(\begin{array}{l} \Rightarrow {S_{ABCD}} = \frac{{\left( {AD + CB} \right).CD}}{2} = \frac{{\left( {AD + CB} \right).\left( {DO + OC} \right)}}{2}\\\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{\left( {1 + 4} \right)\left( {1 + 2} \right)}}{2} = \frac{{15}}{2} = 7,5\;\;\left( {dvdt} \right).\end{array}\)

Vậy diện tích tứ giác ABCD là: \(7,5\;dvdt.\)

Câu 8:

Phương pháp:

Giải bài toàn bằng cách lập phương trình hoặc hệ phương trình:

+) Gọi ẩn và đặt điều kiện cho ẩn.

+) Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết.

+) Dựa vào giả thiết của bài toán để lập phương trình hoặc hệ phương trình.

+) Giải phương trình hoặc hê phương trình vừa lập để  tìm ẩn và đối chiếu với điều kiện của ẩn rồi kết luận.

Cách giải:

Nhân dịp Tết Thiếu nhi 01/06, một nhóm học sinh cần chia đều một số lượng quyển vở thành các phần quà để tặng cho các em nhỏ tại một mái ấm tình thương. Nếu mỗi phần quà giảm 2 quyển thì các em sẽ có thêm 2 phần quà nữa, còn nếu mỗi phần quà giảm 4 quyển thì các em sẽ có thêm 5 phần quà nữa. Hỏi ban đầu có bao nhiêu phần quà và mỗi phần quà có bao nhiêu quyển vở?

Gọi số phần quà ban đầu là \(x\) (phần) \(\left( {x \in N*} \right).\)

Gọi số quyển vở có trong mỗi phần quà là \(y\) (quyển vở) \(\left( {y \in N*} \right).\)

\( \Rightarrow \) Tổng số quyển vở của nhóm học sinh có là: \(xy\) (quyển).

Nếu mỗi phần quà giảm 2 quyển thì số có thêm 2 phần quà nữa nên ta có phương trình:

\(xy = \left( {x + 2} \right)\left( {y - 2} \right) \Leftrightarrow 2y - 2x - 4 = 0 \Leftrightarrow y - x = 2.\;\;\left( 1 \right)\)

Nếu mỗi phần quả giảm 4 quyển thì có thêm 5 phần quà nữa nên ta có phương trình:

\(xy = \left( {x + 5} \right)\left( {y - 4} \right) \Leftrightarrow 5y - 4x - 20 = 0 \Leftrightarrow 5y - 4x = 20\;\;\;\;\left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{ \begin{array}{l}y - x = 2\\5y - 4x = 20\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y - 5x = 10\\5y - 4x = 20\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 10\\y = x + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 10\;\;\left( {tm} \right)\\y = 12\;\;\;\left( {tm} \right)\end{array} \right..\)

Vậy ban đầu có 10 phần quà và mỗi phần quà có 12 quyển vở.

Câu 9 (2,5 điểm)

Cho đường tròn đường kính AB, các điểm C, D nằm trên đường tròn đó sao cho C, D nằm khác phía đối với đường thẳng AB, đồng thời AD > AC. Gọi điểm chính giữa của các cung nhỏ AC và AD lần lượt là M, N; giao điểm của MN với AC, AD lần lượt là H, I; giao điểm của MD và CN là K.

a) Chứng minh \(\widehat {ACN} = \widehat {DMN}\). Từ đó suy ra tứ giác MCKH nội tiếp.

b) Chứng minh KH song song với AD.

c) Tìm hệ thức liên hệ giữa  và  để AK song song với ND.

Phương pháp:

a) Sử dụng tính chất: Các góc nội tiếp chắn các cung bằng nhau thì bằng nhau.

b) Chứng minh hai góc ở vị trí đồng vị bằng nhau.

c) Chứng minh MD là tiếp tuyến của đường tròn (O).

Cách giải:

Cho đường tròn đường kính AB, các điểm C, D nằm trên đường tròn đó sao cho C, D nằm khác phía đối với đường thẳng AB, đồng thời AD > AC. Gọi điểm chính giữa của các cung nhỏ AC và AD lần lượt là M, N; giao điểm của MN với AC, AD lần lượt là H, I; giao điểm của MD và CN là K.

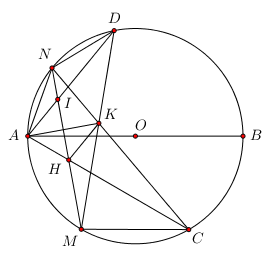
a) Chứng minh \(\widehat {ACN} = \widehat {DMN}\) . Từ đó suy ra tứ giác MCKH nội tiếp.

Ta có:

Góc ACN là góc nội tiếp chắn cung AN; góc DMN là góc nội tiếp chắn cung DN.

Mà cung AN = cung DN (gt)

\( \Rightarrow \widehat {ACN} = \widehat {DMN}\) (Các góc nội tiếp chắn các cung bằng nhau thì bằng nhau).

b) Chứng minh KH song song với AD.

Do đó tứ giác CMHK là tứ giác nội tiếp (Tứ giác có hai góc nội tiếp cùng chắn 1 cung bằng nhau).

\( \Rightarrow \widehat {CHK} = \widehat {CMK} = \widehat {CMD}\) (hai góc nội tiếp cùng chắn cung CK).

Mà \(\widehat {CMD} = \widehat {CAD}\) (hai góc nội tiếp cùng chắn cung CD của đường tròn (O))

\( \Rightarrow \widehat {CHK} = \widehat {CAD}\).

Mà hai góc này ở vị trí đồng vị \( \Rightarrow HK//AD\).

c) Tìm hệ thức liên hệ giữa  và  để AK song song với ND.

Chứng minh tương tự ta có \(AI//KH\)

\( \Rightarrow \) Tứ giác AHKI là hình bình hành (Tứ giác có các cạnh đối song song)

Ta có AK // DN \( \Rightarrow \widehat {IAK} = \widehat {ADN}\) (so le trong)

Lại có \(\widehat {ADN} = \widehat {DMN} = \widehat {AMN} \Rightarrow \widehat {IAK} = \widehat {DMN} = \widehat {KMI} \Rightarrow \) tứ giac AIKM là tứ giác nội tiếp (Tứ giác có hai góc nội tiếp cùng chắn 1 cung bằng nhau).

\( \Rightarrow \widehat {AMN} = \widehat {AKI}\) (hai góc nội tiếp cùng chắn cung AI)

\( \Rightarrow \widehat {IAK} = \widehat {AKI} \Rightarrow \Delta IAK\) cân tại I \( \Rightarrow IA = IK\)

\( \Rightarrow AHKI\) là hình thoi (Hình bình hành có hai cạnh kề bằng nhau).

\( \Rightarrow IH \bot AK\) (hai đường chéo của hình thoi).

\( \Rightarrow MN \bot AK\), mà \(AK//DN \Rightarrow AM \bot ND \Rightarrow \widehat {MND} = {90^0} \Rightarrow \) Góc MND nội tiếp chắn nửa đường tròn.

\( \Rightarrow MD\) là đường kính của đường tròn tâm O.

\( \Rightarrow \) sđ cung MAD = 180 ⁰

\( \Rightarrow \) sđ cung MA + sđ cung AD = 180 ⁰

\( \Rightarrow \) sđ cung \(\frac{{AC}}{2}\) + sđ cung AD = 180 ⁰

Câu 10  (1 điểm)

a) Cho các số thực dương a, b, c thỏa mãn điều kiện \(a + b + c = 3\) . Tìm giá trị nhỏ nhất của biểu thức \(A = 4{a^2} + 6{b^2} + 3{c^2}\)

Áp dụng BĐT Cauchy cho 2 số dương ta có:

\(\begin{array}{l}4\left( {{a^2} + 1} \right) \ge 4.2\sqrt {{a^2}.1}  = 8a\\6\left( {{b^2} + \frac{4}{9}} \right) \ge 6.2\sqrt {{b^2}.\frac{4}{9}}  = 8b\\3\left( {{c^2} + \frac{{16}}{9}} \right) \ge 3.2\sqrt {{c^2}.\frac{{16}}{9}}  = 8c\end{array}\)

Cộng vế theo vế ta có \(A + 4 + \frac{8}{3} + \frac{{16}}{3} \ge 8\left( {a + b + c} \right) = 8.3 = 24\)

Vậy \(A \ge 12\)

Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}{a^2} - 1\\{b^2} = \frac{4}{9}\\{c^2} = \frac{{16}}{9}\\a,b,c \ge 0\\a + b + c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = \frac{2}{3}\\c = \frac{4}{3}\end{array} \right.\)

Vậy \({A_{\min }} = 12 \Leftrightarrow \left( {a;b;c} \right) = \left( {1;\frac{2}{3};\frac{4}{3}} \right)\)

b) Tìm các số nguyên dương a, b biết các phương trình \({x^2} - 2ax - 3b = 0\) và \({x^2} - 2bx - 3a = 0\) , với x là ẩn, đều có nghiệm nguyên.

Xét phương trình \({x^2} - 2ax - 3b = 0\) có \({\Delta _1}' = {a^2} + 3b > 0 \Rightarrow \) Phương trình có hai nghiệm phân biệt \(x = a \pm \sqrt {{a^2} + 3b} \)

Xét phương trình \({x^2} - 2bx - 3a = 0\) có \({\Delta _2}' = {b^2} + 3a > 0 \Rightarrow \) Phương trình có hai nghiệm phân biệt \(x = b \pm \sqrt {{b^2} + 3a} \)

Để cả hai phương trình đều có nghiệm nguyên \( \Leftrightarrow {a^2} + 3b\) và \({b^2} + 3a\) đều là số chinh phương.

Do vai trò của a và b là như nhau, không mất tính tổng quát, ta giả sử \(a \ge b\).

Ta chứng minh \({a^2} + 3b \le {\left( {a + 2} \right)^2}\).

Ta có

\(\begin{array}{l}\,\,\,\,\,{a^2} + 3b < {\left( {a + 2} \right)^2}\\ \Leftrightarrow {a^2} + 3b < {a^2} + 4a + 4\\ \Leftrightarrow 3b < 4a + 4\end{array}\)

Luôn đúng do giả sử \(a \ge b\).

\( \Rightarrow {a^2} < {a^2} + 3b < {\left( {a + 2} \right)^2}\,\,\left( {Do\,\,b > 0} \right)\).

Mà a, b là các số nguyên dương \( \Rightarrow {a^2} + 3b = {\left( {a + 1} \right)^2}\) là số chính phương.

\( \Leftrightarrow 3b = 2a + 1 \Rightarrow a = \frac{{3b - 1}}{2}\)

Thay vào \({\Delta _2}'\) ta có :  \({\Delta _2}' = {b^2} + 3.\frac{{3b - 1}}{2} = {b^2} + \frac{9}{2}b - \frac{3}{2} = {b^2} + 2.b.\frac{9}{4} + \frac{{81}}{{16}} - \frac{{105}}{{16}} = {\left( {b + \frac{9}{4}} \right)^2} - \frac{{105}}{{16}}\) là số chính phương.

Giả sử \({\left( {b + \frac{9}{4}} \right)^2} - \frac{{105}}{{16}} = {x^2}\,\,\left( {x \in Z} \right) \Leftrightarrow \left( {b + \frac{9}{4} - x} \right)\left( {b + \frac{9}{4} + x} \right) = \frac{{105}}{{16}}\)

\(\begin{array}{l} \Leftrightarrow \frac{{4b - 4x + 9}}{4}.\frac{{4b + 4x + 9}}{4} = \frac{{105}}{{16}}\\ \Leftrightarrow \left( {4b - 4x + 9} \right)\left( {4b + 4x + 9} \right) = 5.21 = 1.105\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}4b - 4x + 9 = 5\\4b + 4x + 9 = 21\end{array} \right.\\\left\{ \begin{array}{l}4b - 4x + 9 = 21\\4b + 4x + 9 = 5\end{array} \right.\\\left\{ \begin{array}{l}4b - 4x + 9 = 1\\4b + 4x + 9 = 105\end{array} \right.\\\left\{ \begin{array}{l}4b - 4x + 9 = 105\\4b + 4x + 9 = 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}b = 1\\x = 2\end{array} \right.\\\left\{ \begin{array}{l}b = 1\\x =  - 2\end{array} \right.\\\left\{ \begin{array}{l}b = 11\\x = 13\end{array} \right.\\\left\{ \begin{array}{l}b = 11\\x =  - 13\end{array} \right.\end{array} \right. \Rightarrow \left[ \begin{array}{l}b = 1\\b = 11\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}b = 1\\a = \frac{{3b - 1}}{2} = 1\end{array} \right.\\\left\{ \begin{array}{l}b = 11\\a = \frac{{3b - 1}}{2} = 16\end{array} \right.\end{array} \right.\,\,\,\left( {tm} \right)\end{array}\)

\( \Rightarrow \left( {a;b} \right) \in \left\{ {\left( {1;1} \right);\,\,\left( {16;11} \right)} \right\}\)

Do a, b có vai trò như nhau nên \(\left( {a;b} \right) = \left( {11;16} \right)\) cũng thỏa mãn điều kiện bài toán.

Vậy các cặp số \(\left( {a;b} \right)\) thỏa mãn là \(\left( {1;1} \right);\,\,\left( {16;11} \right);\,\,\left( {11;16} \right)\).