Đề thi vào 10 môn Toán Bắc Ninh năm 2019
Tải vềI. TRẮC NGHIỆM KHÁCH QUAN (3 điểm) Câu 1: Khi
Đề bài
I. TRẮC NGHIỆM KHÁCH QUAN (3 điểm)
Câu 1: Khi \(x = 7\) biểu thức \(\frac{4}{{\sqrt {x + 2} - 1}}\) có giá trị là:
A. \(\frac{1}{2}\) B. \(\frac{4}{{\sqrt 8 }}\) C. \(\frac{4}{3}\) D. \(2\)
Câu 2: Trong các hàm số sau, hàm số nào đồng biến trên \(R\) ?
A. \(y = 1 - x\) B. \(y = 2x - 3\) C. \(y = \left( {1 - \sqrt 2 } \right)x\) D. \(y = - 2x + 6\)
Câu 3: Số nghiệm của phương trình \({x^4} - 3{x^2} + 2 = 0\) là:
A. \(1\) B. \(2\) C. \(3\) D. \(4\)
Câu 4: Cho hàm số \(y = a{x^2}\,\left( {a \ne 0} \right)\). Điểm \(M\left( {1;2} \right)\) thuộc đồ thị hàm số khi
A. \(a = 2\) B. \(a = \frac{1}{2}\) C. \(a = - 2\) D. \(a = \frac{1}{4}\)
Câu 5: Từ điểm \(A\) nằm bên ngoài đường tròn \(\left( O \right)\) kẻ hai tiếp tuyến \(AB,AC\) tới đường tròn (B và C là các tiếp điểm). Kẻ đường kính \(BK.\) Biết \(\angle BAC = {30^0}\) , số đo của cung nhỏ \(CK\) là:
A. \({30^0}\) B. \({60^0}\) C. \({120^0}\) D. \({150^0}\)
Câu 6: Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(H\) là chân đường cao hạ từ đỉnh \(A\) xuống cạnh \(BC\) biết \(AH = \sqrt {12} cm.\,\,\frac{{HB}}{{HC}} = \frac{1}{3}\) . Độ dài đoạn \(BC\) là:
A. \(6cm\) B. \(8cm\) C. \(4\sqrt 3 \) D. \(12cm\)
II. TỰ LUẬN (7 điểm)
Câu 7 (2 điểm):
Cho biểu thức: \(A = \frac{{{{\left( {\sqrt x + 1} \right)}^2} + {{\left( {\sqrt x - 1} \right)}^2}}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} - \frac{{3\sqrt x + 1}}{{x - 1}}\) với \(x \ge 0,\,\,x \ne 1.\)
a) Rút gọn biểu thức \(A.\)
b) Tìm \(x\) là số chính phương để \(2019A\) là số nguyên.
Câu 8 (1 điểm)
An đếm số bài kiểm tra một tiết đạt điểm 9 và điểm 10 của mình thấy nhiều hơn 16 bài. Tổng số điểm của tất cả các bài kiểm tra đạt điểm 9 và điểm 10 đó là 160. Hỏi An được bao nhiêu bài điểm 9 và bao nhiêu bài điểm 10?
Câu 9 ( 2,5 điểm):
Cho đường tròn \(\left( O \right)\) , hai điểm \(A,B\) nằm trên \(\left( O \right)\) sao cho \(\angle AOB = {90^0}\) . Điểm \(G\) nằm trên cung lớn \(AB\) sao cho \(AC > BC\) và tam giác \(ABC\) có ba góc đều nhọn. Các đường cao \(AI,\,BK\) của tam giác \(ABC\) cắt nhau tại điểm \(H\) , \(BK\) cắt \(\left( O \right)\) tại điểm \(N\) (khác điểm B); AI cắt \(\left( O \right)\) tại điểm \(M\)(khác điểm A); NA cắt MB tại điểm D. Chứng minh rằng:
a) Tứ giác \(CIHK\) nội tiếp một đường tròn.
b) \(MN\) là đường kính của đường tròn \(\left( O \right)\)
c) \(OC\) song song với \(DH\).
Câu 10 (1,5 điểm)
a) Cho phương trình \({x^2} - 2mx - 2m - 1 = 0\,\,\left( 1 \right)\) với \(m\) là tham số. Tìm \(m\) để phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\) sao cho \(\sqrt {{x_1} + {x_2}} + \sqrt {3 + {x_1}{x_2}} = 2m + 1\)
b) Cho hai số thực không âm \(a,b\) thỏa mãn \({a^2} + {b^2} = 2\) . Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(M = \frac{{{a^2} + {b^2} + 4}}{{ab + 1}}.\)
Lời giải chi tiết
I. PHẦN TRẮC NGHIỆM (3 điểm)
|
1. D |
2. B |
3. D |
4. A |
5. A |
6. B |
Câu 1
Phương pháp:
Thay \(x = 7\,\,\,\left( {tm} \right)\)vào biểu thức \(\frac{4}{{\sqrt {x + 2} - 1}}\) ta tính được giá trị của biểu thức tại \(x = 7\).
Cách giải:
Điều kiện: \(\left\{ \begin{array}{l}x + 2 \ge 0\\\sqrt {x + 2} - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x \ne - 1\end{array} \right..\)
Thay \(x = 7\,\,\left( {tm} \right)\) vào biểu thức \(\frac{4}{{\sqrt {x + 2} - 1}}\) ta được: \(\frac{4}{{\sqrt {7 + 2} - 1}} = \frac{4}{{3 - 1}} = 2\)
Chọn D.
Câu 2
Phương pháp:
Hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R}\) khi \(a > 0\) , nghịch biến trên \(\mathbb{R}\) khi \(a < 0.\)
Cách giải:
Trong các hàm số đã cho hàm số \(y = 2x - 3\) đồng biến trên \(\mathbb{R}.\)
Chọn B.
Câu 3
Phương pháp:
Giải phương trình rồi kết luận số nghiệm của phương trình.
Cách giải:
\({x^4} - 3{x^2} + 2 = 0\,\,\,\,\,\left( 1 \right)\)
Đặt \(t = {x^2}\,\left( {t \ge 0} \right).\) Khi đó (1) \( \Leftrightarrow {t^2} - 3t + 2 = 0\)
Ta thấy \(1 - 3 + 2 = 0\) . Nên phương trình có nghiệm \(t = 1\,\,\,\left( {TM} \right)\) hoặc \(t = 2\,\,\left( {TM} \right)\)
\( \Rightarrow \left[ \begin{array}{l}{x^2} = 1\\{x^2} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pm 1\\x = \pm \sqrt 2 \end{array} \right.\)
\( \Rightarrow PT\) có 4 nghiệm phân biệt.
Chọn D.
Câu 4
Phương pháp:
Thay tọa độ điểm \(M\left( {1;2} \right)\) vào hàm số tìm ra \(a.\)
Cách giải:
Vì \(M\left( {1;2} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\,\left( {a \ne 0} \right)\) nên ta có: \(2 = a{.1^2}\, \Leftrightarrow a = 2\,\,\left( {tm} \right)\)
Chọn A .
Câu 5
Phương pháp:
+) Tổng 4 góc của tứ giác lồi bằng \({360^0}.\)
+) Sử tính chất góc ở tâm bằng số đo cung bị chắn.
Cách giải:
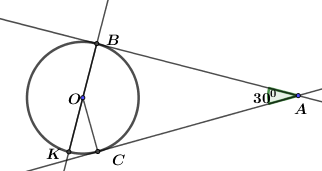
|
Ta có: \(AC,\,\,AB\) là các tiếp tuyến của \(\left( O \right)\) \( \Rightarrow \angle OBA = \angle OCA = {90^0}\) (tính chất tiếp tuyến) Xét tứ giác \(\angle OBAC\) ta có: \(\begin{array}{l}\angle BOC = {360^0} - \left( {\angle OBA + \angle BAC + \angle ACO} \right)\\ = {360^0} - \left( {{{90}^0} + {{90}^0} + {{30}^0}} \right) = {150^0}.\end{array}\) Mà \(\angle BOC + \angle KOC = {180^0}\) (hai góc kề bù) \( \Rightarrow \angle KOC = {180^0} - \angle BOC = {180^0} - {150^0} - {30^0}.\) Mà \(\angle KOC\) là góc ở tâm chắn cung \(CK \Rightarrow sd\,\,cung\,\,CK = \angle KOC = {30^0}.\) Chọn A. |
A. \(6cm\) B. \(8cm\) C. \(4\sqrt 3 \) D. \(12cm\)
Câu 6
Phương pháp:
Sử dụng hệ thức lượng trong tam giác vuông: \(A{H^2} = BH.HC\) để làm bài toán.
Cách giải:
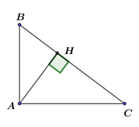
|
Theo đề bài ta có: \(\frac{{HB}}{{HC}} = \frac{1}{3} \Rightarrow HC = 3HB\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại\(A\) có đường cao \(AH\) ta có: \(\begin{array}{l}A{H^2} = BH.HC \Leftrightarrow 12 = BH.3BH \Leftrightarrow B{H^2} = 4 \Leftrightarrow BH = 2\,\,cm.\\ \Rightarrow HC = 3.HB = 3.2 = 6.\\ \Rightarrow BC = HB + HC = 2 + 6 = 8\,\,cm.\end{array}\) Chọn B. |
II. PHẦN TỰ LUẬN (7 điểm)
Câu 7
Phương pháp:
a) Quy đồng mẫu các phân thức rồi rút gọn biểu thức.
b) Số \(x = {k^2}\) là số chính phương.
Cách giải:
Cho biểu thức: \(A = \frac{{{{\left( {\sqrt x + 1} \right)}^2} + {{\left( {\sqrt x - 1} \right)}^2}}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} - \frac{{3\sqrt x + 1}}{{x - 1}}\) với \(x \ge 0,\,\,x \ne 1.\)
a) Rút gọn biểu thức \(A.\)
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
\(\begin{array}{l}A = \frac{{{{\left( {\sqrt x + 1} \right)}^2} + {{\left( {\sqrt x - 1} \right)}^2}}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} - \frac{{3\sqrt x + 1}}{{x - 1}}\\\,\,\,\, = \frac{{x + 2\sqrt x + 1 + x - 2\sqrt x + 1}}{{x - 1}} - \frac{{3\sqrt x + 1}}{{x - 1}}\\\,\,\, = \frac{{2x + 2}}{{x - 1}} - \frac{{3\sqrt x + 1}}{{x - 1}} = \frac{{2x + 2 - 3\sqrt x - 1}}{{x - 1}}\\\,\,\, = \frac{{2x - 3\sqrt x + 1}}{{x - 1}} = \frac{{2x - 2\sqrt x - \sqrt x + 1}}{{x - 1}}\\\,\,\, = \frac{{2\sqrt x \left( {\sqrt x - 1} \right) - \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} = \frac{{\left( {2\sqrt x - 1} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\, = \frac{{2\sqrt x - 1}}{{\sqrt x + 1}}.\end{array}\)
b) Tìm \(x\) là số chính phương để \(2019A\) là số nguyên.
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
Ta có: \(2019A = 2019.\frac{{2\sqrt x - 1}}{{\sqrt x + 1}} = 2019\left( {2 - \frac{3}{{\sqrt x + 1}}} \right) = 4038 - \frac{{6057}}{{\sqrt x + 1}}.\)
Vì \(2019A \in \mathbb{Z} \Rightarrow \sqrt x + 1 \in U\left( {6057} \right)\).
Mà \(\sqrt x + 1 \ge 1\,\,\forall x \ge 0,\,\,x \ne 1 \Rightarrow \sqrt x + 1 \in \left\{ {1;3;9;2019;6057} \right\}\).
TH1: \(\sqrt x + 1 = 1 \Leftrightarrow x = 0\) (tm).
TH2: \(\sqrt x + 1 = 3 \Leftrightarrow \sqrt x = 2 \Leftrightarrow x = 4\,\,\left( {tm} \right)\).
TH3: \(\sqrt x + 1 = 9 \Leftrightarrow \sqrt x = 8 \Leftrightarrow x = 64\,\,\left( {tm} \right)\).
TH4: \(\sqrt x + 1 = 2019 \Leftrightarrow \sqrt x = 2018 \Leftrightarrow x = {2018^2}\,\,\left( {tm} \right)\).
TH5: \(\sqrt x + 1 = 6057 \Leftrightarrow \sqrt x = 6056 \Leftrightarrow x = {6056^2}\,\,\left( {tm} \right)\).
Vậy \(x \in \left\{ {0;\,\,4;\,\,64;\,\,{{2018}^2};\,\,{{6056}^2}} \right\}\).
Câu 8
Phương pháp:
Gọi số bài kiểm tra 1 tiết đạt điểm 9 là \(x\) (bài) \(\left( {x \in \mathbb{N}} \right)\) và số bài kiểm tra 1 tiết đạt điểm 10 là \(y\) (bài) \(\left( {y \in \mathbb{N}} \right)\).
Dựa vào các giả thiết của bài toán, giải bài toán bằng cách lập phương trình và biện luận để giải bài toán.
Cách giải:
Gọi số bài kiểm tra 1 tiết đạt điểm 9 là \(x\) (bài) \(\left( {x \in \mathbb{N}} \right)\) và số bài kiểm tra 1 tiết đạt điểm 10 là \(y\) (bài) \(\left( {y \in \mathbb{N}} \right)\).
Do số bài kiểm tra 1 tiết đạt điểm 9 và điểm 10 nhiều hơn 16 bài nên \(x + y > 16 \Leftrightarrow 9x + 9y > 144\) (1).
Tổng số điểm của \(x\) bài kiểm tra 1 tiết đạt điểm 9 là \(9x\) (điểm).
Tổng số điểm của \(y\) bài kiểm tra 1 tiết đạt điểm 10 là \(10y\) (điểm).
Do tổng số điểm tất cả các bài kiểm tra đạt 9 điểm và 10 điểm là 160 nên ta có phương trình:
\(9x + 10y = 160 \Leftrightarrow 9x = 160 - 10y\).
Thay vào (1) ta có: \(160 - 10y + 9y > 144 \Leftrightarrow 160 - 144 > y \Leftrightarrow y < 16\).
Do \(y \in \mathbb{N} \Rightarrow y \in \left\{ {0;1;2;3;...;15} \right\}\).
Ta có:
\(\begin{array}{l}x \in \mathbb{N} \Rightarrow 9x = 160 - 10y \equiv 0\,\,\left( {\bmod 9} \right) \Leftrightarrow 153 + 7 - 9y - y\,\,\left( {\bmod 9} \right)\\ \Leftrightarrow 7 - y\,\, \equiv 0\,\,\left( {\bmod 9} \right) \Leftrightarrow y \equiv 7\,\,\left( {\bmod 9} \right)\end{array}\)
\( \Rightarrow y = 7 \Rightarrow x = 10\,\,\left( {tm} \right)\).
Vậy số bài kiểm tra 1 tiết đạt điểm 9 là 10 bài và số bài kiểm tra 1 tiết đạt điểm 10 là 7 bài.
Câu 9
Phương pháp:
a) Sử dụng dấu hiệu nhận biết của tứ giác nội tiếp để chứng minh.
b) c) Sử dụng các tính chất của các góc nội tiếp, góc ở tâm cùng chắn một cung ; các tính chất của các đường thẳng song song.
Cách giải:
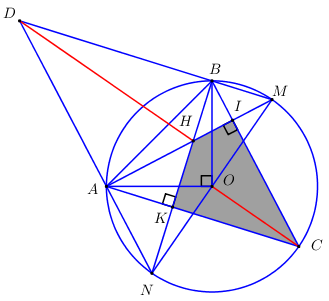
a) Tứ giác \(CIHK\) nội tiếp một đường tròn.
Ta có: \(AI \bot BC \Rightarrow \angle CIH = {90^0},\,\,BK \bot AC \Rightarrow \angle CKH = {90^0}\).
Xét tứ giác \(CIHK\) có : \(\angle CIH + \angle CKH = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(CIKH\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180 0 ).
b) \(MN\) là đường kính của đường tròn \(\left( O \right)\) .
Ta có \(\angle ACB = \angle AMB = \frac{1}{2}\angle AOB = \frac{1}{2}{.90^0} = {45^0}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(AB\)).
Có \(AI \bot BC \Rightarrow \Delta IAC\) vuông tại \(I\), lại có \(\angle ACB = \angle ACI = {45^0} \Rightarrow \Delta IAC\) vuông cân tại \(I \Rightarrow \angle IAC = {45^0}\).
\( \Rightarrow \angle AMB = \angle IAC = {45^0}\). Mà hai góc này ở vị trí so le trong \( \Rightarrow BM//AC\).
Mà \(BK \bot AC\,\,\left( {gt} \right)\) hay \(BN \bot AC \Rightarrow BM \bot BN\) (từ vuông góc đến song song).
\( \Rightarrow \angle MBN = {90^0} \Rightarrow \angle MBN\) nội tiếp chắn nửa đường tròn \( \Rightarrow MN\) là đường kính của đường tròn\(\left( O \right)\).
c) \(OC\) song song với \(DH\) .
Có \(\angle IAC = {45^0}\,\,\left( {cmt} \right) \Rightarrow \angle MAC = {45^0}\).
Mà \(\angle MAC = \frac{1}{2}\angle MOC\) (góc nội tiếp và góc ở tâm cùng chắn cung \(MC\)).
\( \Rightarrow \angle MOC = 2\angle MAC = {2.45^0} = {90^0} \Rightarrow OC \bot OM\) hay \(OC \bot MN\,\,\left( 1 \right)\) .
Ta có \(\angle ANB = \angle ACB = \frac{1}{2}\angle AOB = \frac{1}{2}{.90^0} = {45^0}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(AB\)).
Tam giác \(KBC\) có \(\angle BKC = {90^0};\,\,\angle KCB = \angle ACB = {45^0} \Rightarrow \angle KBC = {45^0}\).
\( \Rightarrow \angle ANB = \angle KBC = {45^0}\). Mà 2 góc này ở vị trí so le trong \( \Rightarrow BC//AN\).
Theo giả thiết ta có \(BC \bot AI \Rightarrow AI \bot AN\) hay \(MA \bot DN\) (từ vuông góc đến song song)
Mặt khác ta có \(BN \bot BM\,\,\left( {cmt} \right) \Rightarrow BN \bot DM\).
Xét tam giác \(DMN\) có: hai đường cao \(MA,\,\,NB\) cắt nhau tại \(H \Rightarrow H\) là trực tâm của tam giác \(DMN\).
\( \Rightarrow DH \bot MN\,\,\left( 2 \right)\).
Từ (1) và (2) \( \Rightarrow OC//DH\) (Từ vuông góc đến song song) (đpcm).
Câu 10
Cách giải:
a) Cho phương trình \({x^2} - 2mx - 2m - 1 = 0\,\,\left( 1 \right)\) với \(m\) là tham số. Tìm m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) sao cho \(\sqrt {{x_1} + {x_2}} + \sqrt {3 + {x_1}{x_2}} = 2m + 1\) .
Ta có: \(\Delta ' = {m^2} + 2m + 1 = {\left( {m + 1} \right)^2}\).
Để phương trình (1) có 2 nghiệm phân biệt thì \(\Delta > 0 \Leftrightarrow {\left( {m + 1} \right)^2} > 0 \Leftrightarrow m \ne - 1\).
Khi \(m \ne - 1\) phương trình (1) có 2 nghiệm phân biệt: \(\left\{ \begin{array}{l}{x_1} = m + m + 1 = 2m + 1\\{x_2} = m - \left( {m + 1} \right) = - 1\end{array} \right.\).
Theo bài ra ta có:
\(\begin{array}{l}\sqrt {{x_1} + {x_2}} + \sqrt {3 + {x_1}{x_2}} = 2m + 1 \Leftrightarrow \sqrt {2m} + \sqrt {3 - \left( {2m + 1} \right)} = 2m + 1 \Leftrightarrow \sqrt {2m} + \sqrt {2 - 2m} = 2m + 1\\ \Leftrightarrow \left\{ \begin{array}{l}2m + 1 \ge 0\\2m \ge 0\\2 - 2m \ge 0\\2m + 2 - 2m + 2\sqrt {2m\left( {2 - 2m} \right)} = 4{m^2} + 4m + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge - \frac{1}{2}\\m \ge 0\\m \le 1\\2\sqrt {2m\left( {2 - 2m} \right)} = 4{m^2} + 4m - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 \le m \le 1\\4\left( {4m - 4{m^2}} \right) = 16{m^4} + 16{m^2} + 1 + 32{m^3} - 8{m^2} - 8m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le m \le 1\\16{m^4} + 32{m^3} + 24{m^2} - 24m + 1 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 \le m \le 1\\\left( {2m - 1} \right)\left( {8{m^3} + 20{m^2} + 22m - 1} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le m \le 1\\\left[ \begin{array}{l}m = \frac{1}{2}\\m \approx 0,044\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \frac{1}{2}\\m \approx 0,044\end{array} \right.\,\,\left( {tm} \right)\end{array}\)
Vậy \(m = \frac{1}{2}\) hoặc \(m \approx 0,044\).
b) Cho hai số thực không âm \(a,\,\,b\) thỏa mãn \({a^2} + {b^2} = 2\) . Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(M = \frac{{{a^3} + {b^3} + 4}}{{ab + 1}}\) .
+) Tìm giá trị nhỏ nhất.
Áp dụng BĐT Cô-si cho 3 số không âm \({a^3},\,\,{b^3},\,\,1\) ta có:
\(\begin{array}{l}{a^3} + {b^3} + 1 \ge 3\sqrt[3]{{{a^3}.{b^3}.1}} = 3ab\\ \Rightarrow {a^3} + {b^3} + 4 \ge 3ab + 3 = 3\left( {ab + 1} \right)\\ \Leftrightarrow \frac{{{a^3} + {b^3} + 4}}{{ab + 1}} \ge 3\,\,\left( {Do\,\,ab + 1 > 0} \right)\\ \Leftrightarrow M \ge 1\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b\\{a^2} + {b^2} = 2\end{array} \right. \Leftrightarrow a = b = 1\).
Vậy \(\min M = 3 \Leftrightarrow a = b = 1\).
+) Tìm giá trị lớn nhất.
Ta có \(ab \ge 0 \Leftrightarrow ab + 1 \ge 1 \Leftrightarrow \frac{1}{{ab + 1}} \le 1 \Leftrightarrow M = \frac{{{a^3} + {b^3} + 4}}{{ab + 1}} \le {a^3} + {b^3} + 4\).
Ta có \(\left\{ \begin{array}{l}a,\,\,b \ge 0\\{a^2} + {b^2} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} \le 2\\{b^2} \le 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le a \le \sqrt 2 \\0 \le b \le \sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le {a^3} \le {a^2}\sqrt 2 \\0 \le {b^3} \le {b^2}\sqrt 2 \end{array} \right.\).
Do đó \({a^3} + {b^3} + 4 \le {a^2}\sqrt 2 + {b^2}\sqrt 2 + 4 = \sqrt 2 \left( {{a^2} + {b^2}} \right) + 4 = 2\sqrt 2 + 4\).
\( \Rightarrow M \le 2\sqrt 2 + 4\).
Dấu "=" xảy ra \( \Leftrightarrow \left[ \begin{array}{l}{a^2} = 2\\{b^2} = 2\\ab = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = \sqrt 2 \\b = 0\end{array} \right.\\\left\{ \begin{array}{l}a = 0\\b = \sqrt 2 \end{array} \right.\end{array} \right.\).
Vậy \(\max M = 2\sqrt 2 + 4 \Leftrightarrow \left\{ \begin{array}{l}a = \sqrt 2 \\b = 0\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}a = 0\\b = \sqrt 2 \end{array} \right.\).