Đề thi vào 10 môn Toán Đắk Lắk năm 2020 — Không quảng cáo

Đề bài

Câu 1:

1) Tính giá trị của biểu thức $M = \sqrt {4{a^2}}  + 3a$ tại $a = 2.$

2) Giải hệ phương trình: $\left\{ \begin{array}{l}x - 2y = 1\\ - x + 3y = 2\end{array} \right..$

3) Giải phương trình: $2{x^2} - 9x + 4 = 0.$

Câu 2:

Cho biểu thức: $P = \left( {\dfrac{1}{{3 + \sqrt x }} + \dfrac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  + 6} \right)}}{{9 - x}}} \right):\dfrac{{2\sqrt x  + 1}}{{6 - \sqrt {4x} }}.$

1) Tìm điều kiện của $x$ để biểu thức $P$ có nghĩa và rút gọn $P.$

2) Tìm các giá trị của $x$ sao cho $\sqrt x$ và $P$ là những số nguyên.

Câu 3:

1) Tìm a, b để đường thẳng $y = ax + b$ song song với đường thẳng $y = 4x + 5$ và cắt đồ thị hàm số $y = {x^2}$ tại hai điểm $A\left( {{x_1};{y_1}} \right)$, $B\left( {{x_2};{y_2}} \right)$ phân biệt thỏa mãn $x_1^2 + x_2^2 = 10$.

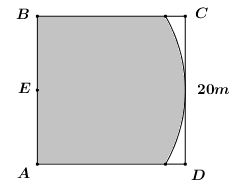
2) Một vườn có hình vuông ABCD có cạnh 20m như hình vẽ. Người ta buộc một con dê bằng sợi dây thừng dài 20m tại trung điểm E của cạnh AB. Tính diện tích phần cỏ mà con dê có thể ăn được (phần tô đậm trên hình vẽ) (Kết quả làm tròn đến hai chữ số thập phân).

Câu 4:

Cho hai đường tròn bằng nhau $\left( {O;\,\,R} \right)$ và $\left( {O';\,\,R} \right)$ cắt nhau tại hai điểm $A$ và $B$ sao cho $AB = R.$ Kẻ đường kính $AC$ của đường tròn $\left( O \right).$ Gọi $E$ là một điểm bất kỳ trên cung nhỏ $BC\,\,\left( {E \ne B,\,\,C} \right).$ $CB$ và $EB$ lần lượt cắt đường tròn $\left( {O'} \right)$ tại các điểm thứ hai là $D$ và $F.$

1) Chứng minh $\angle AFD = {90^0}.$

2) Chứng minh $AE = AF.$

3) Gọi $P$ là giao điểm của $CE$ và $FD.$ Gọi $Q$ là giao điểm của $AP$ và $EF.$ Chứng minh $AP$ là đường trung trực của $EF.$

4) Tính tỉ số $\dfrac{{AQ}}{{AP}}.$

Câu 5:

Cho $a,\,\,b,\,\,c$ là các số thực dương thỏa mãn $a + b + c = 1$. Tìm giá trị nhỏ nhất của biểu thức

$Q = \dfrac{{{{\left( {1 - c} \right)}^2}}}{{\sqrt {2{{\left( {b + c} \right)}^2} + bc} }} + \dfrac{{{{\left( {1 - a} \right)}^2}}}{{\sqrt {2{{\left( {c + a} \right)}^2} + ca} }} + \dfrac{{{{\left( {1 - b} \right)}^2}}}{{\sqrt {2{{\left( {a + b} \right)}^2} + ab} }}$

Lời giải chi tiết

Câu 1 (2 điểm)

Cách giải:

1) Tính giá trị của biểu thức $M = \sqrt {4{a^2}}  + 3a$ tại $a = 2.$

Khi $a = 2$ ta có: $M = \sqrt {{{4.2}^2}}  + 3.2 = \sqrt {16}  + 6 = 4 + 6 = 10.$

Vậy khi $a = 2$ thì $M = 10.$

2) Giải hệ phương trình: $\left\{ \begin{array}{l}x - 2y = 1\\ - x + 3y = 2\end{array} \right..$

$\left\{ \begin{array}{l}x - 2y = 1\\ - x + 3y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x = 1 + 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 + 2.3\\y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 7\\y = 3\end{array} \right.$

Vậy hệ phương trình có nghiệm duy nhất $\left( {x;\,\,y} \right) = \left( {7;\,\,3} \right).$

3) Giải phương trình: $2{x^2} - 9x + 4 = 0.$

Phương trình  $2{x^2} - 9x + 4 = 0$ có: $\Delta  = {\left( { - 9} \right)^2} - 4.2.4 = 49 > 0$

$\Rightarrow$ Phương trình có hai nghiệm phân biệt: $\left[ \begin{array}{l}{x_1} = \dfrac{{9 - \sqrt {49} }}{4} = \dfrac{1}{2}\\{x_2} = \dfrac{{9 + \sqrt {49} }}{4} = 4\end{array} \right.$

Vậy phương trình có tập nghiệm là: $S = \left\{ {\dfrac{1}{2};\,\,4} \right\}.$

Câu 2 (2 điểm)

Cách giải:

Cho biểu thức: $P = \left( {\dfrac{1}{{3 + \sqrt x }} + \dfrac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  + 6} \right)}}{{9 - x}}} \right):\dfrac{{2\sqrt x  + 1}}{{6 - \sqrt {4x} }}.$

1) Tìm điều kiện của $x$ để biểu thức $P$ có nghĩa và rút gọn $P.$

Điều kiện: $\left\{ \begin{array}{l}x \ge 0\\9 - x \ne 0\\6 - \sqrt {4x}  \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ne 9\\4x \ne 36\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ne 9\end{array} \right..$

$\begin{array}{l}P = \left( {\dfrac{1}{{3 + \sqrt x }} + \dfrac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  + 6} \right)}}{{9 - x}}} \right):\dfrac{{2\sqrt x  + 1}}{{6 - \sqrt {4x} }}\\\,\,\,\,\, = \left[ {\dfrac{1}{{3 + \sqrt x }} + \dfrac{{x + 7\sqrt x  + 6}}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}}} \right]:\dfrac{{2\sqrt x  + 1}}{{6 - 2\sqrt x }}\\\,\,\,\,\, = \dfrac{{3 - \sqrt x  + x + 7\sqrt x  + 6}}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}}.\dfrac{{2\left( {3 - \sqrt x } \right)}}{{2\sqrt x  + 1}}\\\,\,\,\,\, = \dfrac{{x + 6\sqrt x  + 9}}{{3 + \sqrt x }}.\dfrac{2}{{2\sqrt x  + 1}}\\\,\,\,\, = \dfrac{{{{\left( {\sqrt x  + 3} \right)}^2}}}{{3 + \sqrt x }}.\dfrac{2}{{2\sqrt x  + 1}}\\\,\,\,\, = \dfrac{{2\left( {\sqrt x  + 3} \right)}}{{2\sqrt x  + 1}} = \dfrac{{2\sqrt x  + 6}}{{2\sqrt x  + 1}}.\end{array}$

Vậy $P = \dfrac{{2\sqrt x  + 6}}{{2\sqrt x  + 1}}$ khi $x \ge 0,\,\,x \ne 9.$

2) Tìm các giá trị của $x$ sao cho $\sqrt x$ và $P$ là những số nguyên.

Điều kiện: $x \ge 0,\,\,x \ne 9.$

Để $\sqrt x$ là số nguyên thì $x$ phải là số nguyên và là số chính phương.

Ta có:  $P = \dfrac{{2\sqrt x  + 6}}{{2\sqrt x  + 1}} = \dfrac{{2\sqrt x  + 1 + 5}}{{2\sqrt x  + 1}} = 1 + \dfrac{5}{{2\sqrt x  + 1}}.$

Để $P \in \mathbb{Z}$ thì $\dfrac{5}{{2\sqrt x  + 1}} \in \mathbb{Z}$ $\Rightarrow 5\,\, \vdots \,\,\left( {2\sqrt x  + 1} \right)$ hay $2\sqrt x  + 1 \in U\left( 5 \right)$

Mà $U\left( 5 \right) = \left\{ { \pm 1;\,\, \pm 5} \right\}$

Với mọi $x \ge 0,\,\,x \ne 9$ ta có: $2\sqrt x  + 1 \ge 1$

$\begin{array}{l} \Rightarrow 2\sqrt x  + 1 \in \left\{ {1;\,\,5} \right\}\\ \Rightarrow \left[ \begin{array}{l}2\sqrt x  + 1 = 1\\2\sqrt x  + 1 = 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2\sqrt x  = 0\\2\sqrt x  = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt x  = 0\\\sqrt x  = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 4\end{array} \right.\end{array}$

Ta thấy $x \in \left\{ {0;\,\,4} \right\}$ thỏa mãn điều kiện $x \ge 0,\,\,x \ne 9,\,\,x$ là số nguyên và là số chính phương.

Vậy $x \in \left\{ {0;\,\,4} \right\}$ thỏa mãn bài toán.

Câu 3 (2,0 điểm)

Cách giải:

1) Tìm a, b để đường thẳng $y = ax + b$ song song với đường thẳng $y = 4x + 5$ và cắt đồ thị hàm số $y = {x^2}$ tại hai điểm $A\left( {{x_1};{y_1}} \right)$ , $B\left( {{x_2};{y_2}} \right)$ phân biệt thỏa mãn $x_1^2 + x_2^2 = 10$ .

Vì đường thẳng $y = ax + b$ song song với đường thẳng $y = 4x + 5$ nên $\left\{ \begin{array}{l}a = 4\\b \ne 5\end{array} \right.$.

Khi đó phương trình đường thẳng cần tìm có dạng $y = 4x + b\,\,\left( {b \ne 5} \right)$.

Xét phương trình hoành độ giao điểm của đường thẳng $y = 4x + b\,\,\left( {b \ne 5} \right)$ và parabol $y = {x^2}$:

${x^2} = 4x + b \Leftrightarrow {x^2} - 4x - b = 0\,\,\left( * \right)$

Để đường thẳng $y = 4x + b\,\,\left( {b \ne 5} \right)$ cắt parabol $y = {x^2}$ tại 2 điểm phân biệt $A\left( {{x_1};{y_1}} \right)$ , $B\left( {{x_2};{y_2}} \right)$ thì phương trình (*) phải có 2 nghiệm phân biệt ${x_1},\,\,{x_2}$.

$\Rightarrow \Delta ' = {\left( { - 2} \right)^2} + b = 4 + b > 0 \Leftrightarrow b >  - 4$.

Áp dụng định lí Vi-ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}{x_2} =  - b\end{array} \right.$.

Theo bài ra ta có:

$\begin{array}{l}\,\,\,\,\,\,x_1^2 + x_2^2 = 10\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\\ \Leftrightarrow {4^2} + 2b = 10\\ \Leftrightarrow 16 + 2b = 10\\ \Leftrightarrow 2b =  - 6\\ \Leftrightarrow b =  - 3\,\,\left( {tm} \right)\end{array}$

Vậy $a = 4,\,\,b =  - 3$.

2) Một vườn có hình vuông ABCD có cạnh 20m như hình vẽ. Người ta buộc một con dê bằng sợi dây thừng dài 20m tại trung điểm E của cạnh AB. Tính diện tích phần cỏ mà con dê có thể ăn được (phần tô đậm trên hình vẽ) (Kết quả làm tròn đến hai chữ số thập phân).

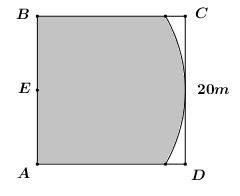
Gọi hai điểm $M,\,\,N$ như hình vẽ.

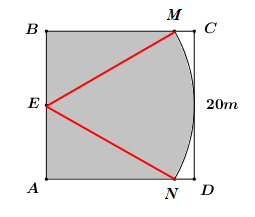
Ta có: $EM = EN = 20m$.

Vì $E$ là trung điểm của $AB$ nên $EA = EB = \dfrac{1}{2}AB = 10\,\,\left( m \right)$.

Áp dụng định lí Pytago trong các tam giác vuông ta có:

$\begin{array}{l}B{M^2} = E{M^2} - E{B^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = {20^2} - {10^2} = 300\\ \Rightarrow BM = \sqrt {300}  = 10\sqrt 3 \,\,\left( m \right)\end{array}$

Tương tự ta có: $AN = BM = 10\sqrt 3 \,\,\left( m \right)$.

$\Rightarrow {S_{\Delta BEM}} = \dfrac{1}{2}BE.BM = \dfrac{1}{2}.10.10\sqrt 3  = 50\sqrt 3 \,\,\left( {{m^2}} \right)$

${S_{\Delta AEN}} = \dfrac{1}{2}AE.AN = \dfrac{1}{2}.10.10\sqrt 3  = 50\sqrt 3 \,\,\left( {{m^2}} \right)$.

Xét tam giác vuông $BEM$ ta có:

$\begin{array}{l}\cos \angle BEM = \dfrac{{BE}}{{BM}} = \dfrac{{10}}{{20}} = \dfrac{1}{2}\\ \Rightarrow \angle BEM = {60^0}\end{array}$

Tương tự xét tam giác vuông $AEN$ ta có:

$\begin{array}{l}\cos \angle AEN = \dfrac{{AE}}{{EN}} = \dfrac{{10}}{{20}} = \dfrac{1}{2}\\ \Rightarrow \angle AEN = {60^0}\end{array}$

Ta có:

$\begin{array}{l}\angle BEM + \angle AEN + \angle MEN = {180^0}\\ \Rightarrow \angle MEN = {180^0} - \angle BEM - \angle AEN\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - {60^0} - {60^0}\\ \Rightarrow \angle MEN = {60^0}\end{array}$

Diện tích hình quạt $EMN$, bán kính $20m$ là: ${S_{qEMN}} = \dfrac{{\pi {R^2}.60}}{{360}} = \dfrac{{\pi {{.20}^2}}}{6} = \dfrac{{200\pi }}{3}\,\,\left( {{m^2}} \right)$.

Vậy diện tích phần cỏ mà con dê có thể ăn là:

$\begin{array}{l}S = {S_{\Delta BEM}} + {S_{\Delta AEN}} + {S_{qEMN}}\\\,\,\,\, = 50\sqrt 3  + 50\sqrt 3  + \dfrac{{200\pi }}{3}\\\,\,\,\, \approx 382,64\,\,\left( {{m^2}} \right)\end{array}$

Câu 4 (3 điểm)

Cách giải:

Cho hai đường tròn bằng nhau $\left( {O;\,\,R} \right)$ và $\left( {O';\,\,R} \right)$ cắt nhau tại hai điểm $A$ và $B$ sao cho $AB = R.$ Kẻ đường kính $AC$ của đường tròn $\left( O \right).$ Gọi $E$ là một điểm bất kỳ trên cung nhỏ $BC\,\,\left( {E \ne B,\,\,C} \right).$ $CB$ và $EB$ lần lượt cắt đường tròn $\left( {O'} \right)$ tại các điểm thứ hai là $D$ và $F.$

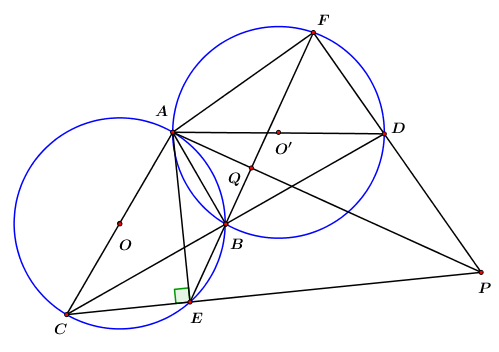
1) Chứng minh $\angle AFD = {90^0}.$

Ta có: $\angle ABC$ là góc nội tiếp chắn nửa đường tròn $\left( {O;\,\,R} \right)$

$\Rightarrow \angle ABC = {90^0}$ $\Rightarrow \angle ABD = {90^0}$ (hai góc kề bù)

Mà $\angle ABD$ là góc nội tiếp chắn nửa đường tròn $\left( {O';\,\,R} \right)$

$\Rightarrow$ $AD$ là đường kính của $\left( {O';\,\,R} \right)$

Lại có:$\angle AFD$ là góc nội tiếp chắn cung $AD$

$\Rightarrow \angle AFD = {90^0}$ (đpcm).

2) Chứng minh $AE = AF.$

Ta có: $\angle AEB = \angle ACB$ (hai góc nội tiếp cùng chắn cung $AB$ của $\left( O \right)$)

Hay $\angle AEF = \angle ACD\,\,\,\,\left( 1 \right)$

$\angle AFB = \angle ADB$ (hai góc nội tiếp cùng chắn cung $AB$ của $\left( {O'} \right)$)

Hay $\angle AFE = \angle ADC\,\,\,\,\left( 2 \right)$

Ta có: $AD = AC = 2R$ $\Rightarrow \Delta ADC$ cân tại $A$ (định nghĩa tam giác cân)

$\Rightarrow \angle ACD = \angle ADC\,\,\,\left( 3 \right)$

Từ (1), (2) và (3) suy ra: $\angle AEF = \angle AFE$

$\Rightarrow \Delta AEF$ là tam giác cân.

$\Rightarrow AE = AF$ (tính chất tam giác cân).

3) Gọi $P$ là giao điểm của $CE$ và $FD.$ Gọi $Q$ là giao điểm của $AP$ và $EF.$ Chứng minh $AP$ là đường trung trực của $EF.$

Ta có: $AE = AF\,\,\left( {cmt} \right)$ $\Rightarrow A$ thuộc đường trung trực của $EF.$ (4)

Xét $\Delta AEP$ và $\Delta AFP$ ta có:

$\begin{array}{l}AE = AF\,\,\left( {cmt} \right)\\\angle AEP = \angle AFD = {90^0}\\AP\,\,chung\end{array}$

$\Rightarrow \Delta AEP = \Delta AFP\,\,\,\left( {ch - cgv} \right)$

$\Rightarrow PE = PF$ (hai cạnh tương ứng bằng nhau)

$\Rightarrow P$ thuộc đường trung trực của $EF.$ (5)

Từ (4) và (5) suy ra: $AP$ là đường trung trực của $EF.$ (đpcm)

4) Tính tỉ số $\dfrac{{AQ}}{{AP}}.$

Ta có: $AP$ là đường trung trực của $EF.$ (cmt)

$\Rightarrow AP \bot EF = \left\{ Q \right\}.$

Áp dụng hệ thức lượng cho $\Delta AFP$ vuông tại $F$ có đường cao $FQ$ ta có:

$\begin{array}{l}A{F^2} = AQ.AP \Rightarrow AP = \dfrac{{A{F^2}}}{{AQ}}\\ \Rightarrow \dfrac{{AQ}}{{AP}} = \dfrac{{A{Q^2}}}{{A{F^2}}}\end{array}$

Xét $\Delta AFQ$ vuông tại $Q$ ta có:

$\begin{array}{l}\sin \angle AFQ = \dfrac{{AQ}}{{AF}} \Rightarrow \sin \angle ADB = \dfrac{{AQ}}{{AF}} = \dfrac{{AB}}{{AD}} = \dfrac{1}{2}\\ \Rightarrow {\left( {\dfrac{{AQ}}{{AF}}} \right)^2} = \dfrac{1}{4}\\ \Rightarrow \dfrac{{AQ}}{{AP}} = \dfrac{1}{4}.\end{array}$

Vậy $\dfrac{{AQ}}{{AP}} = \dfrac{1}{4}.$

Câu 5 (1,0 điểm)

Cách giải:

Cho $a,\,\,b,\,\,c$ là các số thực dương thỏa mãn $a + b + c = 1$ . Tìm giá trị nhỏ nhất của biểu thức

$Q = \dfrac{{{{\left( {1 - c} \right)}^2}}}{{\sqrt {2{{\left( {b + c} \right)}^2} + bc} }} + \dfrac{{{{\left( {1 - a} \right)}^2}}}{{\sqrt {2{{\left( {c + a} \right)}^2} + ca} }} + \dfrac{{{{\left( {1 - b} \right)}^2}}}{{\sqrt {2{{\left( {a + b} \right)}^2} + ab} }}$

Do $\left\{ \begin{array}{l}a,\,\,b,\,\,c > 0\\a + b + c = 1\end{array} \right. \Rightarrow 0 < a,\,\,b,\,\,c < 1$.

Ta có:

$\begin{array}{l}bc \le {\left( {\dfrac{{b + c}}{2}} \right)^2} = \dfrac{{{{\left( {b + c} \right)}^2}}}{4}\\ \Rightarrow 2{\left( {b + c} \right)^2} + bc \le 2{\left( {b + c} \right)^2} + \dfrac{{{{\left( {b + c} \right)}^2}}}{4} = \dfrac{{9{{\left( {b + c} \right)}^2}}}{4}\\ \Rightarrow \sqrt {2{{\left( {b + c} \right)}^2} + bc}  \le \sqrt {\dfrac{{9{{\left( {b + c} \right)}^2}}}{4}}  = \dfrac{{3\left( {b + c} \right)}}{2}\,\,\left( {Do\,\,b,\,\,c > 0} \right)\\ \Rightarrow \dfrac{{{{\left( {1 - c} \right)}^2}}}{{\sqrt {2{{\left( {b + c} \right)}^2} + bc} }} \ge \dfrac{{{{\left( {1 - c} \right)}^2}}}{{\dfrac{{3\left( {b + c} \right)}}{2}}} = \dfrac{2}{3}.\dfrac{{{{\left( {1 - c} \right)}^2}}}{{\left( {b + c} \right)}} = \dfrac{2}{3}.\dfrac{{{{\left( {1 - c} \right)}^2}}}{{1 - a}}\end{array}$

Chứng minh tương tự ta có:

$\begin{array}{l}\dfrac{{{{\left( {1 - a} \right)}^2}}}{{\sqrt {2{{\left( {c + a} \right)}^2} + ca} }} \ge \dfrac{2}{3}.\dfrac{{{{\left( {1 - a} \right)}^2}}}{{1 - b}}\\\dfrac{{{{\left( {1 - b} \right)}^2}}}{{\sqrt {2{{\left( {a + b} \right)}^2} + ab} }} \ge \dfrac{2}{3}.\dfrac{{{{\left( {1 - b} \right)}^2}}}{{1 - c}}\end{array}$

Khi đó ta có:

$\begin{array}{l}Q = \dfrac{{{{\left( {1 - c} \right)}^2}}}{{\sqrt {2{{\left( {b + c} \right)}^2} + bc} }} + \dfrac{{{{\left( {1 - a} \right)}^2}}}{{\sqrt {2{{\left( {c + a} \right)}^2} + ca} }} + \dfrac{{{{\left( {1 - b} \right)}^2}}}{{\sqrt {2{{\left( {a + b} \right)}^2} + ab} }}\\\,\,\,\,\, \ge \dfrac{2}{3}\left[ {\dfrac{{{{\left( {1 - c} \right)}^2}}}{{1 - a}} + \dfrac{{{{\left( {1 - a} \right)}^2}}}{{1 - b}} + \dfrac{{{{\left( {1 - b} \right)}^2}}}{{1 - c}}} \right]\\\,\,\,\,\, \ge \dfrac{2}{3}.\dfrac{{{{\left( {1 - c + 1 - a + 1 - b} \right)}^2}}}{{1 - a + 1 - b + 1 - c}} = \dfrac{2}{3}.\dfrac{{{{\left[ {3 - \left( {a + b + c} \right)} \right]}^2}}}{{3 - \left( {a + b + c} \right)}} = \dfrac{2}{3}.\dfrac{{{{\left( {3 - 1} \right)}^2}}}{{3 - 1}} = \dfrac{4}{3}\end{array}$

Dấu “=” xảy ra $\Leftrightarrow \left\{ \begin{array}{l}a = b = c\\a + b + c = 1\end{array} \right. \Leftrightarrow a = b = c = \dfrac{1}{3}$.

Vậy $\min Q = \dfrac{4}{3} \Leftrightarrow a = b = c = \dfrac{1}{3}$.