Đề thi vào 10 môn Toán Đắk Lắk năm 2021 — Không quảng cáo

Đề bài

Câu 1 (1,5 điểm)

1) Giải phương trình: $2{x^2} + 5x - 3 = 0.$

2) Cho hàm số $y = \left( {m - 1} \right)x + 2021.$ Tìm tất cả các giá trị của tham số m để đồ thị hàm số đồng biến trên $\mathbb{R}$.

3) Cho $a = 1 + \sqrt 2$ và $b = 1 - \sqrt 2$. Tính giá trị của biểu thức $P = a + b - 2ab.$

Câu 2 ( 2,0 điểm):

Cho biểu thức: $P = \dfrac{{2\sqrt x  - 9}}{{x - 5\sqrt x  + 6}} - \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \dfrac{{2\sqrt x  + 1}}{{\sqrt x  - 3}}$ với $x \ge 0,x \ne 4,x \ne 9$

1) Rút gọn biểu thức $P$

2) Tìm tất cả các giá trị của $x$ để $P > 1$

Câu 3 (2,0 điểm):

1) Trong mặt phẳng tọa độ $Oxy$, viết phương trình đường thẳng $\Delta$ đi qua điểm $A\left( {1; - 2} \right)$song song với đường thẳng $y = 2x - 1$.

2) Trong mặt phẳng tọa độ $Oxy$, cho Parabol $\left( P \right):y = {x^2}$ và đường thẳng $\left( d \right):y = 2\left( {m - 1} \right)x - m + 3$. Gọi ${x_1},{x_2}$ lần lượt là hoành độ giao điểm của đường thẳng $\left( d \right)$ và Parabol $\left( P \right)$. Tìm giá trị nhỏ nhất của biểu thức $M = x_1^2 + x_2^2$.

Câu 4 (3,5 điểm):

Trên nửa đường tròn tâm $O$đường kính $AB$ với $AB = 2022$, lấy điểm $C$ ($C$ khác $A$ và $B$) từ $C$ kẻ $CH$ vuông góc với $AB$$\left( {H \in AB} \right)$. Gọi $D$ là điểm bất kì trên đoạn $CH$($D$ khác $C,H$), đường thẳng $AD$ cắt nửa đường tròn tại điểm thứ hai $E$.

1)  Chứng minh $BHDE$ nội tiếp.

2) Chứng minh $AD.EC = CD.AC$

3) Chứng minh $AD.AE + BH.BA = {2022^2}$

4) Khi điểm $C$ di động trên nửa đường tròn $C$ khác $A,\,B$ và điểm chính giữa cung $AB$, xác định vị trí điểm $C$ sao cho chu vi tam giác $COH$ đạt giá trị lớn nhất.

Câu 5 (1,0 điểm):

Cho $a \ge 1348,\,\,b \ge 1348$. Chứng minh ${a^2} + {b^2} + ab \ge 2022\left( {a + b} \right)$.

Lời giải chi tiết

Câu 1 (1,5 điểm) 1) Giải phương trình: $2{x^2} + 5x - 3 = 0.$ 2) Cho hàm số $y = \left( {m - 1} \right)x + 2021.$ Tìm tất cả các giá trị của tham số m để đồ thị hàm số đồng biến trên $\mathbb{R}$. 3) Cho $a = 1 + \sqrt 2$ và $b = 1 - \sqrt 2$. Tính giá trị của biểu thức $P = a + b - 2ab.$

Phương pháp:

1) Tính $\Delta  = {b^2} - 4ac$ (hoặc $\Delta ' = {\left( {b'} \right)^2} - ac$), sử dụng công thức nghiệm của phương trình bậc hai một ẩn: ${x_{1,2}} = \dfrac{{ - b \pm \sqrt \Delta  }}{{2a}}$ (hoặc ${x_{1,2}} = \dfrac{{ - b' \pm \sqrt {\Delta '} }}{a}$), tính được nghiệm của phương trình, kết luận.

2) Hàm số $y = ax + b$ đồng biến trên $\mathbb{R} \Leftrightarrow a > 0$

3) Thay $a = 1 + \sqrt 2$ và $b = 1 - \sqrt 2$ vào $P$, sau đó tính toán.

Cách giải:

1) Xét phương trình $2{x^2} + 5x - 3 = 0$

Ta có: $\Delta  = {5^2} + 24 = 49 > 0$

$\Rightarrow$ Phương trình có hai nghiệm: ${x_1} = \dfrac{{ - 5 + \sqrt {49} }}{4} = \dfrac{1}{2}$; ${x_2} = \dfrac{{ - 5 - \sqrt {49} }}{4} =  - 3$

Vậy phương trình có tập nghiệm: $S = \left\{ { - 3;\,\,\dfrac{1}{2}} \right\}$.

2) Hàm số $y = \left( {m - 1} \right)x + 2021$ đồng biến trên $\mathbb{R}$ khi và chỉ khi: $m - 1 > 0 \Leftrightarrow m > 1$

Vậy với $m > 1$ thì hàm số đồng biến trên $\mathbb{R}$.

3) Thay $a = 1 + \sqrt 2$ và  $b = 1 - \sqrt 2$ vào $P = a + b - 2ab$ ta được:

$\begin{array}{l}P = 1 + \sqrt 2  + 1 - \sqrt 2  - 2\left( {1 + \sqrt 2 } \right)\left( {1 - \sqrt 2 } \right)\\\,\,\,\, = 2 - 2\left[ {1 - {{\left( {\sqrt 2 } \right)}^2}} \right]\\\,\,\, = 2 - 2\left( {1 - 2} \right)\\\,\,\, = 2 + 2 = 4.\end{array}$

Vậy $P = 4$  khi $a = 1 + \sqrt 2$ và $b = 1 - \sqrt 2 .$

Câu 2 ( 2,0 điểm): Cho biểu thức: $P = \dfrac{{2\sqrt x  - 9}}{{x - 5\sqrt x  + 6}} - \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \dfrac{{2\sqrt x  + 1}}{{\sqrt x  - 3}}$ với $x \ge 0,x \ne 4,x \ne 9$ 1) Rút gọn biểu thức $P$ 2) Tìm tất cả các giá trị của $x$ để $P > 1$

Phương pháp:

1) Xác định mẫu thức chung của biểu thức

Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.

2) Vì $P > 1 \Leftrightarrow P - 1 > 0$

Rút gọn $P - 1$

$\dfrac{{f\left( x \right)}}{{g\left( x \right)}} > 0$ khi $f\left( x \right)$ và $g\left( x \right)$  cùng âm hoặc dương.

Cách giải:

1) ĐKXĐ: $x \ge 0,x \ne 4,x \ne 9$

$\begin{array}{l}P = \dfrac{{2\sqrt x  - 9}}{{x - 5\sqrt x  + 6}} - \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \dfrac{{2\sqrt x  + 1}}{{\sqrt x  - 3}}\\\,\,\,\,\, = \dfrac{{2\sqrt x  - 9}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}} - \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \dfrac{{2\sqrt x  + 1}}{{\sqrt x  - 3}}\\\,\,\,\,\, = \dfrac{{2\sqrt x  - 9 - \left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right) + \left( {2\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\\\,\,\,\,\, = \dfrac{{2\sqrt x  - 9 - \left( {x - 9} \right) + \left( {2x - 3\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\\\,\,\,\,\, = \dfrac{{2\sqrt x  - 9 - x + 9 + 2x - 3\sqrt x  - 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\\\,\,\,\,\, = \dfrac{{x - \sqrt x  - 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\\\,\,\,\, = \dfrac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}} = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 3}}\end{array}$

Vậy với $x \ge 0,\,\,x \ne 4,\,\,x \ne 9$ ta có $B = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 3}}.$

b) Điều kiện: $x \ge 0,\,\,x \ne 4,\,\,x \ne 9$

$\begin{array}{l}P > 1 \Leftrightarrow \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 3}} > 1\\ \Leftrightarrow \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 3}} - 1 > 0\\ \Leftrightarrow \dfrac{{\sqrt x  + 1 - \left( {\sqrt x  - 3} \right)}}{{\sqrt x  - 3}} > 0\\ \Leftrightarrow \dfrac{4}{{\sqrt x  - 3}} > 0\\ \Leftrightarrow \sqrt x  - 3 > 0\,\,\,\left( {do\,\,\,4 > 0} \right)\\ \Leftrightarrow \sqrt x  > 3\\ \Leftrightarrow x > 9\end{array}$

Kết hợp với điều kiện xác định ta được $x > 9$ thì $P > 1$

Vậy $x > 9$ thì $P > 1.$

Câu 3 (2,0 điểm): 1) Trong mặt phẳng tọa độ $Oxy$, viết phương trình đường thẳng $\Delta$ đi qua điểm $A\left( {1; - 2} \right)$song song với đường thẳng $y = 2x - 1$. 2) Trong mặt phẳng tọa độ $Oxy$, cho Parabol $\left( P \right):y = {x^2}$ và đường thẳng $\left( d \right):y = 2\left( {m - 1} \right)x - m + 3$. Gọi ${x_1},{x_2}$ lần lượt là hoành độ giao điểm của đường thẳng $\left( d \right)$ và Parabol $\left( P \right)$. Tìm giá trị nhỏ nhất của biểu thức $M = x_1^2 + x_2^2$.

Phương pháp:

1) Viết phương trình đường thẳng $\Delta$ biết $\Delta$ đi qua điểm $A\left( {{x_A};{y_A}} \right)$ và song song với $d:y = a'x + b'$ ($a';b'$  đã biết)

Gọi phương trình đường thẳng$\Delta$ là $y = ax + b\,\,\,\left( {a \ne 0} \right)$

Vì $\Delta //d \Rightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$

$\Rightarrow d:y = a'x + b$

$\Delta$ đi qua điểm $A\left( {{x_A};{y_A}} \right)$, từ đó tìm được $b$, đối chiếu điều kiện ở trên

Kết luận phương trình đường thẳng cần tìm.

2) Xét phương trình hoành độ giao điểm giữa $\left( P \right)$ và $\left( d \right)$  $\left( 1 \right)$

Để $\left( P \right)$ cắt $\left( d \right)$ tại hai điểm phân biệt $\Leftrightarrow \left( 1 \right)$ có hai nghiệm phân biệt ${x_1},\,\,{x_2}$.

$\Leftrightarrow \Delta  > 0$

Áp dụng hệ thức Vi – ét, tính được ${x_1} + {x_2};{x_1}.{x_2}$ theo $m$

Thay vào $M = x_1^2 + x_2^2$, vận dụng hằng đẳng thức tìm được giá trị nhỏ nhất của $M$

Cách giải:

1) Gọi phương trình đường thẳng$\Delta$ là $y = ax + b\,\,\,\left( {a \ne 0} \right)$

Vì $\Delta$ song song với đường thẳng $y = 2x - 1$ nên $\left\{ \begin{array}{l}a = 2\\b \ne  - 1\end{array} \right.$.

Vì $\Delta$ đi qua điểm $A\left( {1; - 2} \right)$ nên ta có: $- 2 = a + b$.

Thay $a = 2$ vào ta được: $- 2 = 2 + b \Leftrightarrow b =  - 4\,\,\,\left( {tm} \right)$.

Vậy đường thẳng $\Delta$ cần tìm có phương trình là $y = 2x - 4$.

2) Hoành độ giao điểm của $\left( d \right)$ và $\left( P \right)$ là nghiệm của phương trình:

${x^2} = 2\left( {m - 1} \right)x - m + 3 \Leftrightarrow {x^2} - 2\left( {m - 1} \right)x + m - 3 = 0\,\,\left( * \right)$

Phương trình (*) có:

$\begin{array}{l}\Delta ' = {\left( {m - 1} \right)^2} - \left( {m - 3} \right) = {m^2} - 2m + 1 - m + 3\\\,\,\,\,\,\, = {m^2} - 3m + 4 = {\left( {m - \dfrac{3}{2}} \right)^2} + \dfrac{7}{4} > 0\,\,\,\,\forall m \in \mathbb{R}\end{array}$

$\Rightarrow$ Phương trình (*) luôn có hai nghiệm phân biệt ${x_1},\,\,{x_2}$ với mọi $m$.

$\Rightarrow$ $\left( d \right)$ luôn cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1},{x_2}$ với mọi $m$.

Áp dụng định lí Vi-et ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right)\\{x_1}{x_2} = m - 3\end{array} \right.$

Khi đó ta có:

$\begin{array}{l}\,\,\,\,\,\,M = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\\ \Leftrightarrow M = {\left[ {2\left( {m - 1} \right)} \right]^2} - 2.\left( {m - 3} \right)\\ \Leftrightarrow M = 4{m^2} - 8m + 4 - 2m + 6\\ \Leftrightarrow M = 4{m^2} - 10m + 10\\ \Leftrightarrow M = {\left( {2m} \right)^2} - 2.2m.\dfrac{5}{2} + {\left( {\dfrac{5}{2}} \right)^2} + \dfrac{{15}}{4}\end{array}$

$\Leftrightarrow M = {\left( {2m - \dfrac{5}{2}} \right)^2} + \dfrac{{15}}{4} \ge \dfrac{{15}}{4}\,\,\forall m$ (Vì ${\left( {2m - \dfrac{5}{2}} \right)^2} \ge 0\,\,\forall m$)

Vậy ${M_{\min }} = \dfrac{{15}}{4}$. Dấu “=” xảy ra khi và chỉ khi $2m = \dfrac{5}{2} \Leftrightarrow m = \dfrac{5}{4}$.

Câu 4 (3,5 điểm): Trên nửa đường tròn tâm $O$đường kính $AB$ với $AB = 2022$, lấy điểm $C$ ($C$ khác $A$ và $B$) từ $C$ kẻ $CH$ vuông góc với $AB$$\left( {H \in AB} \right)$. Gọi $D$ là điểm bất kì trên đoạn $CH$($D$ khác $C,H$), đường thẳng $AD$ cắt nửa đường tròn tại điểm thứ hai $E$. 1)  Chứng minh $BHDE$ nội tiếp. 2) Chứng minh $AD.EC = CD.AC$ 3) Chứng minh $AD.AE + BH.BA = {2022^2}$ 4) Khi điểm $C$ di động trên nửa đường tròn $C$ khác $A,\,B$ và điểm chính giữa cung $AB$, xác định vị trí điểm $C$ sao cho chu vi tam giác $COH$ đạt giá trị lớn nhất.

Phương pháp:

1) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng ${180^0}$ là tứ giác nội tiếp.

2) Ta sẽ chứng minh:

3) Ta sẽ chứng minh:

Ta có: $AD.AE + BH.AB = AH.AB + BH.AB = \left( {AH + BH} \right).AB = A{B^2} = {2022^2}\,\,\left( {dpcm} \right)$

4) Tính chu vi của tam giác $COH$

Chu vi tam giác $COH$  đạt giá trị lớn nhất $\Leftrightarrow$ $OH + CH$ đạt giá trị lớn nhất $\Leftrightarrow$ ${\left( {OH + CH} \right)^2}$ đạt giá trị lớn nhất

Áp dụng định lý cô-si cho $OH,CH$ tìm được giá trị lớn nhất.

Cách giải:

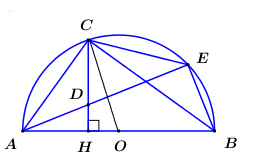
1) Trong $\left( O \right)$ ta có $\angle AEB = {90^0}$( góc nội tiếp chắn nửa đường tròn)

Tứ giác $BHDE$ có: $\angle BED + \angle BHD = {180^0}$.

Suy ra tứ giác $BHDE$ nội tiếp (dhnb).

2) Ta có:

$\angle ACD = \angle CBA$ (cùng phụ với $\angle BCD$).

$\angle CEA = \angle CBA$ (2 góc nội tiếp cùng chắn cung $CA$).

$\Rightarrow \angle ACD = \angle CEA$.

Xét tam giác $ACD$ và tam giác $AEC$ có: $\left\{ \begin{array}{l}\angle CAD = \angle CAE\\\angle ACD = \angle CEA\,\,\,\left( {cmt} \right)\end{array} \right.$

Suy ra  $\Rightarrow \dfrac{{AD}}{{AC}} = \dfrac{{CD}}{{EC}} \Rightarrow AD.EC = CD.AC\,\,\left( {dpcm} \right)$.

3) Xét tam giác $AHD$ và tam giác $AEB$ có: $\left\{ \begin{array}{l}\angle AHD = \angle AEB = {90^0}\\\angle HAD = \angle BAE\end{array} \right.$

.

Suy ra $\dfrac{{AH}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow AD.AE = AH.AB$$\left( 1 \right)$

Ta có:

$\begin{array}{l}AD.AE + BH.AB = AH.AB + BH.AB\\ = \left( {AH + BH} \right).AB = A{B^2} = {2022^2}\,\,\left( {dpcm} \right)\end{array}$

4) Chu vi tam giác $COH$ là: $CO + OH + CH = \dfrac{{AB}}{2} + OH + CH = 1011 + OH + CH$

Chu vi tam giác $COH$  đạt giá trị lớn nhất $\Leftrightarrow$ $OH + CH$ đạt giá trị lớn nhất $\Leftrightarrow$ ${\left( {OH + CH} \right)^2}$ đạt giá trị lớn nhất

Ta có: $0 < OH,CH < OC = 1011$.

Áp dụng định lý cô-si cho $OH,CH$ ta có:

${\left( {OH + CH} \right)^2} \le 2\left( {O{H^2} + C{H^2}} \right) = 2.O{C^2} \Rightarrow OH + CH \le OC\sqrt 2$

Dấu “=” xảy ra khi $OH = CH = \dfrac{{OC\sqrt 2 }}{2}$ hay $\Delta OHC$ vuông cân tại $H$ $\Rightarrow \angle COA = {45^0}$.

Vậy chu vi tam giác $COH$ đạt giá trị lớn nhất khi góc $COA$ bằng ${45^0}$.

Câu 5 (1,0 điểm): Cho $a \ge 1348,\,\,b \ge 1348$. Chứng minh ${a^2} + {b^2} + ab \ge 2022\left( {a + b} \right)$.

Phương pháp:

Xuất phát từ bất đẳng thức: ${a^2} + {b^2} \ge 2ab$.

Cách giải:

Ta có: ${a^2} + {b^2} \ge 2ab \Leftrightarrow {a^2} + {b^2} + ab \ge 3ab$

$\Rightarrow {a^2} + {b^2} + ab \ge \dfrac{3}{2}ab + \dfrac{3}{2}ab \ge \dfrac{3}{2}.a.1348 + \dfrac{3}{2}.b.1348$(Do $a \ge 1348,\,\,b \ge 1348$)

$\Rightarrow {a^2} + {b^2} + ab \ge 2022\left( {a + b} \right)\,\,\,\left( {dpcm} \right)$.

Dấu “=” xảy ra khi $a = b = 1348$.