Đề thi vào 10 môn Toán Nam Định năm 2023
Tải vềPhần I: Trắc nghiệm (2 điểm) Câu 1: Điều kiện xác định của biểu thức \(\frac{5}{{\sqrt {x - 2023} {\rm{ \;}} + 1}}\) là A. \(x \ge 2023\). B. \(x > 2023\). C. \(x < 2023\). D. \(x \le 2023\).
Đề bài
Phần I: Trắc nghiệm (2 điểm)
Câu 1: Điều kiện xác định của biểu thức \(\frac{5}{{\sqrt {x - 2023} {\rm{ \;}} + 1}}\) là
A. \(x \ge 2023\).
B. \(x > 2023\).
C. \(x < 2023\).
D. \(x \le 2023\).
Câu 2: Hàm số nào sau đây đồng biến với mọi \(x \in \mathbb{R}\) ?
A. \(y = \left( {1 - \sqrt 5 } \right){x^2}\).
B. \(y = x + 3\).
C. \(y = \left( {2 - \sqrt 7 } \right)x + 2\).
D. \(y = {x^2}\).
Câu 3: Phương trình \(2{x^2} - x - 1 = 0\) có hai nghiệm \({x_1},{x_2}\) trong đó \({x_1} < {x_2}\). Giá trị \(2{x_1} + {x_2}\) bằng
A. 0
B. \( - 1,5\)
C. -2
D. 2
Câu 4: Với giá trị nào của \(m\) thì đường thẳng \(y = \left( {m - 1} \right)x + 2\) đi qua điểm \(A\left( { - 1;1} \right)\) ?
A. \(m = 0\).
B. \(m = {\rm{ \;}} - 1\).
C. \(m = {\rm{ \;}} - 2\).
D. \(m = 2\).
Câu 5: Số nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - 3y = 2}\end{array}} \right.\) là
A. 2
B. 0
C. 1
D. vô số.
Câu 6: Cho \(\Delta ABC\) vuông tại \(A\), biết \(AC = 6,BC = 10\). Khi đó \({\rm{tan}}B\) có giá trị bằng
A. \(\frac{3}{4}\).
B. \(\frac{3}{5}\).
C. \(\frac{4}{3}\).
D. \(\frac{5}{3}\).
Câu 7: Một hình nón có bán kính đáy bằng \(4\;{\rm{cm}}\), chiều cao bằng \(6\;{\rm{cm}}\). Thể tích của hình nón đã cho là
A. \(96\pi {\rm{c}}{{\rm{m}}^3}\).
B. \(32\pi {\rm{c}}{{\rm{m}}^3}\).
C. \(30\pi {\rm{c}}{{\rm{m}}^3}\).
D. \(36\pi {\rm{c}}{{\rm{m}}^3}\).
Câu 8: Cho \(\Delta ABC\) có \(\angle BAC = 45^\circ \), nội tiếp trong đường tròn tâm \(O\) bán kính \(2\;{\rm{cm}}\). Diện tích tam giác OBC bằng bao nhiêu
A. \(1\;{\rm{c}}{{\rm{m}}^2}\).
B. \(4\;{\rm{c}}{{\rm{m}}^2}\).
C. \(2\;{\rm{c}}{{\rm{m}}^2}\).
D. \(2\sqrt 2 \;{\rm{c}}{{\rm{m}}^2}\).
Phần II. Tự luận (8 điểm)
Câu 9:
a) Chứng minh đẳng thức \(\sqrt {27} {\rm{ \;}} - 2\sqrt {12} {\rm{ \;}} + \sqrt {4 - 2\sqrt 3 } {\rm{ \;}} = {\rm{ \;}} - 1\).
b) Rút gọn biểu thức \(A = \left( {\frac{{9 - \sqrt x }}{{x - 9}} + \frac{2}{{\sqrt x {\rm{ \;}} + 3}}} \right):\frac{{\sqrt x {\rm{ \;}} + 1}}{{\sqrt x {\rm{ \;}} - 3}}\) với \(x \ge 0\) và \(x \ne 9\).
Câu 10:
a) Tìm tọa độ giao điểm của đồ thị hai hàm số \(y = {x^2}\) và \(y = {\rm{ \;}} - 2x + 3\).
b) Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + 6m - 4 = 0\) (với \(m\) là tham số). Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) thoả mãn \(x_1^2 - x_2^2 = 3{x_1}{x_2}\left( {{x_2} - {x_1}} \right)\).
Câu 11: Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 3y = 4}\\{\frac{1}{{x - 4}} + \frac{1}{y} = 1.}\end{array}} \right.\)
Câu 12:
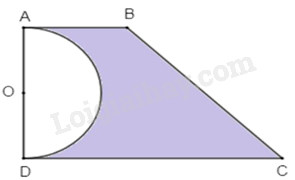
1) Một mảnh vườn hình thang \(ABCD\) có \(\angle BAD = \angle ADC = 90^\circ \), \(AB = 3{\rm{\;m}},AD = 5{\rm{\;m}},DC = 7{\rm{\;m}}\). Người ta trồng hoa trên phần đất là nửa hình tròn tâm \(O\) đường kính \(AD\), phần còn lại của mảnh vườn để trồng cỏ (phần tô đậm trong hình vẽ bên). Tính diện tích phần đất trồng cỏ (kết quả làm tròn đến chũ số thập phân thư hai, lấy \(\pi \approx 3,14\) ).
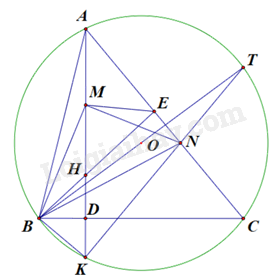
2) Cho tam giác \(ABC\) nhọn \((AB < AC)\) nội tiếp \(\left( O \right)\). Hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Gọi \(M\) là trung điểm của \(AH\), đường thẳng đi qua \(M\) vuông góc với \(BM\) cắt \(AC\) tại \(N\). Gọi \(K\) là giao điểm thứ hai của \(AH\) với đường tròn tâm \(O\).
a) Chứng minh bốn điểm \(B,M,E,N\) cùng thuộc một đường tròn và \(\angle MBN = \angle KAC\).
b) Kéo dài \(KN\) cắt đường tròn \(\left( O \right)\) tại \(T\). Chứng minh tam giác \(BHK\) cân và ba điểm \(B,O,T\) thẳng hàng.
Câu 13:
a) Giải phương trình \({x^2} + 4x = 2\sqrt {1 + 3x} + \sqrt {2x - 1} \).
b) Cho \(x,y,z\) là các số thực dương thỏa mãn \(x + y + z = 1\).
Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{{x + yz}}{{y + z}} + \frac{{y + zx}}{{z + x}} + \frac{{z + xy}}{{x + y}}.\)
-----HẾT-----
Lời giải chi tiết
Phần I: Trắc nghiệm
|
1.A |
2.B |
3.A |
4.D |
5.C |
6.A |
7.B |
8.C |
Câu 1 (NB):
Phương pháp:
Điều kiện xác định của \(\sqrt {f(x)} \) là \(f(x) \ge 0\)
Cách giải:
Điều kiện xác định của biểu thức \(\frac{5}{{\sqrt {x - 2023} {\rm{ \;}} + 1}}\) là \(x - 2023 \ge 0 \Leftrightarrow x \ge 2023\)
Chọn A.
Câu 2 (NB):
Phương pháp:
Hàm số \(y = ax + b(a \ne 0)\) đồng biến với mọi \(x \in \mathbb{R}\) khi \(a > 0\)
Cách giải:
Hàm số \(y = x + 3\) đồng biến với mọi \(x \in \mathbb{R}\)
Chọn B.
Câu 3 (TH):
Phương pháp:
Giải PT bậc hai một ẩn bằng cách nhẩm nghiệm:
Nếu \(a + b + c = 0\) thì PT có một nghiệm là 1; nghiệm còn lại bằng \(\frac{c}{a}\)
Cách giải:
Xét \(2{x^2} - x - 1 = 0\) có \(a + b + c = 2 + ( - 1) + ( - 1) = 0\)
Mà \({x_1} < {x_2}\) nên PT có \(\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - 1}}{2}}\\{{x_2} = 2}\end{array}} \right. \Rightarrow 2.{x_1} + {x_2} = 2.\frac{{ - 1}}{2} + 1 = 0\)
Chọn A.
Câu 4 (NB):
Phương pháp:
Thay tọa độ điểm \(A\left( { - 1;1} \right)\) vào đường thẳng \(y = \left( {m - 1} \right)x + 2\)
Cách giải:
Thay tọa độ điểm \(A\left( { - 1;1} \right)\) vào đường thẳng \(y = \left( {m - 1} \right)x + 2\) ta được:
\(1 = (m - 1).( - 1) + 2 \Leftrightarrow {\rm{ \;}} - m + 3 = 1 \Leftrightarrow m = 2\)
Chọn D.
Câu 5 (NB):
Phương pháp:
Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ax + by = c}\\{a'x + b'y = c'}\end{array}} \right.\):
Có nghiệm duy nhất \( \Leftrightarrow \frac{a}{{a'}} \ne \frac{b}{{b'}}\);
Vô nghiệm \( \Leftrightarrow \frac{a}{{a'}} = \frac{b}{{b'}} \ne \frac{c}{{c'}}\);
Có vô số nghiệm \( \Leftrightarrow \frac{a}{{a'}} = \frac{b}{{b'}} = \frac{c}{{c'}}\).
Cách giải:
Xét hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - 3y = 2}\end{array}} \right.\) có \(\frac{2}{1} \ne \frac{1}{{ - 3}}\) nên hệ phương trình có nghiệm duy nhất
Chọn C.
Câu 6 (TH):
Phương pháp:
Áp dụng định lí Py-ta-go \(\Delta ABC\) vuông tại \(A\) tìm cạnh AB.
Với công thức lượng giác \({\rm{tan}}B = \frac{{AC}}{{AB}}\)
Cách giải:
Áp dụng định lí Py-ta-go \(\Delta ABC\) vuông tại \(A\) có: \(AB = \sqrt {B{C^2} - A{C^2}} {\rm{ \;}} = \sqrt {{{10}^2} - {6^2}} {\rm{ \;}} = 8\)
\(\tan B = \frac{{AC}}{{AB}} = \frac{6}{8} = \frac{3}{4}\)
Chọn A.
Câu 7 (NB):
Phương pháp:
Công thức thể tích hình nón \(V = \frac{1}{3}\pi {R^2}h\) với R là bán kính, h là chiều cao.
Cách giải:
Một hình nón có bán kính đáy bằng \(4\;{\rm{cm}}\), chiều cao bằng \(6\;{\rm{cm}}\) có thể tích là: \(V = \frac{1}{3}\pi {.4^2}.6 = 32\pi (c{m^3})\)
Chọn B.
Câu 8 (TH):
Phương pháp:
Góc nội tiếp có số đo bằng một nửa góc ở tâm cùng chắn một cung.
Diện tích tam giác OBC bằng \(\frac{1}{2}OB.OC = \frac{1}{2}{R^2}\)
Cách giải:
Xét (O) có \(\angle BOC = 2.\angle BAC = 2.45^\circ = 90^\circ \) (cùng chắn cung BC)
Suy ra tam giác OBC vuông tại O
Diện tích tam giác OBC bằng \(\frac{1}{2}OB.OC = \frac{1}{2}{R^2} = \frac{1}{2}{.2^2} = 2(c{m^2})\)
Chọn C.
Phần II: Tự luận
Câu 9 (TH):
Phương pháp:
a) Thực hiện phép tính với căn bậc hai.
b) Rút gọn biểu thức chứa căn bậc hai.
Cách giải:
a) \(\sqrt {27} {\rm{ \;}} - 2\sqrt {12} {\rm{ \;}} + \sqrt {4 - 2\sqrt 3 } {\rm{ \;}} = 3\sqrt 3 {\rm{ \;}} - 4\sqrt 3 {\rm{ \;}} + \sqrt {{{(\sqrt 3 {\rm{ \;}} - 1)}^2}} \) \( = {\rm{ \;}} - \sqrt 3 {\rm{ \;}} + \left| {\sqrt 3 {\rm{ \;}} - 1} \right| = {\rm{ \;}} - \sqrt 3 {\rm{ \;}} + \sqrt 3 {\rm{ \;}} - 1 = {\rm{ \;}} - 1\)
Vậy \(\sqrt {27} {\rm{ \;}} - 2\sqrt {12} {\rm{ \;}} + \sqrt {4 - 2\sqrt 3 } {\rm{ \;}} = {\rm{ \;}} - 1\)
b) Với \(x \ge 0\) và \(x \ne 9\) ta có:
\(A = \left( {\frac{{9 - \sqrt x }}{{\left( {\sqrt x {\rm{ \;}} - 3} \right)\left( {\sqrt x {\rm{ \;}} + 3} \right)}} + \frac{2}{{\sqrt x {\rm{ \;}} + 3}}} \right):\frac{{\sqrt x {\rm{ \;}} + 1}}{{\sqrt x {\rm{ \;}} - 3}}\)
\( = \frac{{9 - \sqrt x {\rm{ \;}} + 2\left( {\sqrt x {\rm{ \;}} - 3} \right)}}{{\left( {\sqrt x {\rm{ \;}} - 3} \right)\left( {\sqrt x {\rm{ \;}} + 3} \right)}}:\frac{{\sqrt x {\rm{ \;}} + 1}}{{\sqrt x {\rm{ \;}} - 3}} = \frac{{\sqrt x {\rm{ \;}} + 3}}{{\left( {\sqrt x {\rm{ \;}} - 3} \right)\left( {\sqrt x {\rm{ \;}} + 3} \right)}}:\frac{{\sqrt x {\rm{ \;}} + 1}}{{\sqrt x {\rm{ \;}} - 3}}\)
\( = \frac{{\sqrt x {\rm{ \;}} + 3}}{{\left( {\sqrt x {\rm{ \;}} - 3} \right)\left( {\sqrt x {\rm{ \;}} + 3} \right)}} \cdot \frac{{\sqrt x {\rm{ \;}} - 3}}{{\sqrt x {\rm{ \;}} + 1}}\)
\( = \frac{{\sqrt x {\rm{ \;}} + 3}}{{\left( {\sqrt x {\rm{ \;}} - 3} \right)\left( {\sqrt x {\rm{ \;}} + 3} \right)}} \cdot \frac{{\sqrt x {\rm{ \;}} - 3}}{{\sqrt x {\rm{ \;}} + 1}}\)
\( = \frac{1}{{\sqrt x {\rm{ \;}} + 1}}\).
Vậy \(A = \frac{1}{{\sqrt x {\rm{ \;}} + 1}}\) với \(x \ge 0\) và \(x \ne 9\).
Câu 10 (TH):
Phương pháp:
a) Xét phương trình hoành độ giao điểm của hai đồ thị.
b) Công thức \(\Delta ' = {\left( {\frac{b}{a}} \right)^2} - a.c\)
PT bậc hai một ẩn có hai nghiệm phân biệt khi \(\Delta {\rm{ \;}} > 0\)
Hệ thức Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
a) Xét phương trình hoành độ giao điểm của đồ thị hai hàm số \(y = {x^2}\) và \(y = {\rm{ \;}} - 2x + 3\) là:
\(\begin{array}{*{20}{l}}{{x^2} = {\rm{ \;}} - 2x + 3}\\{ \Leftrightarrow {x^2} + 2x - 3 = 0}\\{ \Leftrightarrow {x^2} + 3x - x - 3 = 0}\\{ \Leftrightarrow x(x + 3) - (x + 3) = 0}\\{ \Leftrightarrow (x - 1)(x + 3) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 1 = 0}\\{x + 3 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = {\rm{ \;}} - 3}\end{array}} \right.} \right.}\end{array}\)
Với \(x = 1 \Rightarrow y = {1^2} = 1\)
Với \(x = {\rm{ \;}} - 3 \Rightarrow y = {( - 3)^2} = 9\)
b) Xét phương trình \({x^2} - 2(m + 1)x + 6m - 4 = 0\)
Ta có: \(\Delta ' = {(m + 1)^2} - (6m - 4) = {m^2} + 2m + 1 - 6m + 4\)
\( = {m^2} - 4m + 5 = {(m - 2)^2} + 1 > 0\) với mọi \(m\).
Suy ra phương trình (1) có 2 nghiệm phân biệt với mọi \(m\).
Khi đó, theo hệ thức Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2m + 2}\\{{x_1}{x_2} = 6m - 4}\end{array}} \right.\)
Theo giả thiết: \(x_1^2 - x_2^2 = 3{x_1}{x_2}\left( {{x_2} - {x_1}} \right)\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2}} \right) + 3{x_1}{x_2}\left( {{x_1} - {x_2}} \right) = 0}\\{ \Leftrightarrow \left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2} + 3{x_1}{x_2}} \right) = 0}\\{ \Leftrightarrow {x_1} + {x_2} + 3{x_1}{x_2} = 0\left( {{\rm{do}}{x_1} \ne {x_2}} \right)}\\{ \Rightarrow 2m + 2 + 3(6m - 4) = 0}\\{ \Leftrightarrow 2m + 2 + 18m - 12 = 0}\\{ \Leftrightarrow 20m - 10 = 0}\\{ \Leftrightarrow 20m = 10}\end{array}\)
Câu 11 (NB):
Phương pháp:
Giải hệ phương trình bằng phương pháp thế
Cách giải:
Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 3y = 4}\\{\frac{1}{{x - 4}} + \frac{1}{y} = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4 - 3y{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (1)}\\{\frac{1}{{x - 4}} + \frac{1}{y} = 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (2)}\end{array}} \right.} \right.\)
Thay (1) vào (2) ta được:
\(\begin{array}{*{20}{l}}{\frac{1}{{4 - 3y - 4}} + \frac{1}{y} = 1}\\{ \Leftrightarrow {\rm{ \;}} - \frac{1}{{3y}} + \frac{1}{y} = 1}\\{ \Leftrightarrow \frac{2}{{3y}} = 1}\\{ \Leftrightarrow y = \frac{2}{3}.}\\{ \Rightarrow x = 4 - 3 \cdot \frac{2}{3} = 2.}\end{array}\)
Vậy hệ phương trình có nghiệm duy nhất \((x;y) = \left( {2;\frac{2}{3}} \right)\)
Câu 12 (VD):
Phương pháp:
1) Diện tích hình thang bằng: đáy lớn đáy nhỏ ta đem cộng vào, thế rồi nhân với chiều cao, chia đôi lấy nửa thế nào cũng ra.
Diện tích hình tròn đường kính d là \(S = \pi .{\left( {\frac{d}{2}} \right)^2}\)
Diện tích đất trồng còn lại bằng diện tích hình thang trừ đi nửa diện tích hình tròn.
2) a)
- Chứng minh tứ giác BMEN nội tiếp vì có 2 đỉnh kề nhau cùng nhìn một cạnh dưới một góc bằng nhau.
- Sử dụng tính chất góc ngoài tại đỉnh E bằng góc trong tại đỉnh đối diện của tứ giác nội tiếp MBEN.
Sử dụng tính chất đường trung tuyến trong tam giác vuông AHE.
b)
- Chứng minh \(\angle BHD = \angle BCE\) vì cùng phụ với góc \(\angle HBD\)
Chứng minh \(\angle BKA = \angle BCA\) vì là hai góc nội tiếp cùng chắn cung AB
Từ đó suy ra được tam giác \(BHK\) cân tại B
- Chứng minh tứ giác BMNK nội tiếp vì có 2 đỉnh liên tiếp cùng nhìn một cạnh dưới một góc bằng nhau.
Suy ra tổng 2 góc đối bằng \(180^\circ \), suy ra được \(\angle BKT = 90^\circ \Rightarrow \) BT là đường kính
Suy ra B, O, T thẳng hàng
Cách giải:
1) Diện tích hình thang ABCD là \(\frac{{\left( {AB + DC} \right).AD}}{2} = \frac{{\left( {3 + 7} \right).5}}{2} = 25\;{{\rm{m}}^2}\).
Diện tích nửa hình tròn đường kính AD là \(\frac{1}{2}\pi .{\left( {\frac{5}{2}} \right)^2} = \frac{{\pi .{{(2,5)}^2}}}{2} = \frac{{25\pi }}{8}{m^2}\).
Diện tích phần đất trồng cỏ là \(25 - \frac{{25\pi }}{8} \approx 15,19{m^2}\).
a) Ta có: \(\angle BMN = \angle BEN = 90^\circ (gt)\).
Mà \({\rm{M}},{\rm{E}}\) là hai đỉnh kề nhau cùng nhìn \({\rm{BN}}\) dưới hai góc bằng nhau.
Suy ra BMEN là tứ giác nội tiếp (dhnb)
Hay \({\rm{B}},{\rm{M}},{\rm{E}},{\rm{N}}\) cùng thuộc một đường tròn (dpcm.
Vì BMEN là tứ giác nội tiếp (cmt) nên \(\angle MBN = \angle AEM\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
Xét tam giác \({\rm{AHE}}\) vuông tại \({\rm{E}}\), có đường trung tuyến \({\rm{EM}}\) ứng với cạnh huyền \({\rm{AH}}\) \( \Rightarrow ME = \frac{1}{2}AH = MA = MH\).
\( \Rightarrow \Delta MAE\) cân tại \({\rm{M}}\) (định nghĩa)
\( \Rightarrow \angle EAM = \angle MAE = \angle KAC\) (tính chất)
Vậy \(\angle MBN = \angle KAC(dpcm)\).
b) Xét tam giác BHD vuông tại \({\rm{D}}\) có: \(\angle BHD + \angle HBD = 90^\circ \).
Xét tam giác \({\rm{BEC}}\) vuông tại \({\rm{E}}\) có: \(\angle BCE + \angle HBD = 90^\circ \).
\( \Rightarrow \angle BHD = \angle BCE = \angle BCA.\)
Mà \(\angle BKH = \angle BKA = \angle BCA\) (hai góc nội tiếp cùng chắn cung \({\rm{AB}}\) ).
\( \Rightarrow \angle BHD = \angle BKH.\)
\( \Rightarrow BHK\) cân tại \({\rm{B}}\) (đpcm).
Ta có \(\angle BHK = \angle MHE = \angle MEH = \angle MNB \Rightarrow \angle BKM = \angle BNM\).
Do đó tứ giác BMNK nội tiếp.
\( \Rightarrow \angle BMN + \angle BKN = 180^\circ \Rightarrow \angle BKN = \angle BKT = 90^\circ \)
\( \Rightarrow K\) thuộc đường tròn đường kính BT.
Mà \(B,K,T \in (O) \Rightarrow BT\) là đường kính của \((O)\)
\( \Rightarrow B,O,T\) thẳng hàng.
Câu 13 (VDC):
Phương pháp:
a) Phương pháp nhẩm nghiệm, thêm bớt.
Sử dụng phương pháp liên hợp: \(A - B = \frac{{{A^2} - {B^2}}}{{A + B}};A + B = \frac{{{A^2} - {B^2}}}{{A - B}}\)
Đưa về dạng tích A.B = 0
b) Từ giả thiết \(x + y + z = 1\), chứng minh \(\left\{ {\begin{array}{*{20}{l}}{x + yz = \left( {x + y} \right)\left( {x + z} \right)}\\{y + zx = \left( {y + z} \right)\left( {y + x} \right)}\\{z + xy = \left( {z + x} \right)\left( {z + y} \right)}\end{array}} \right.\)
Thay vảo biểu thức P.
Đặt \(x + y = a,y + z = b,z + x = c \Rightarrow a,b,c > 0\)
Áp dụng BĐT Cosi cho 2 số âm.
Cách giải:
a) ĐКХĐ: \(\left\{ {\begin{array}{*{20}{l}}{1 + 3x \ge 0}\\{2x - 1 \ge 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge {\rm{ \;}} - \frac{1}{3}}\\{x \ge \frac{1}{2}}\end{array} \Leftrightarrow x \ge \frac{1}{2}} \right.} \right.\)
Ta có: \({x^2} + 4x = 2\sqrt {1 + 3x} {\rm{ \;}} + \sqrt {2x - 1} \)
\( \Leftrightarrow {x^2} + 4x - 5 = 2(\sqrt {1 + 3x} {\rm{ \;}} - 2) + (\sqrt {2x - 1} {\rm{ \;}} - 1)\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow (x - 1)(x + 5) = \frac{{2(1 + 3x - 4)}}{{\sqrt {1 + 3x} {\rm{ \;}} + 2}} + \frac{{2x - 1 - 1}}{{\sqrt {2x - 1} {\rm{ \;}} + 1}}}\\{ \Leftrightarrow (x - 1)(x + 5) = \frac{{6(x - 1)}}{{\sqrt {1 + 3x} {\rm{ \;}} + 2}} + \frac{{2(x - 1)}}{{\sqrt {2x - 1} {\rm{ \;}} + 1}}}\end{array}\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow (x - 1)\left( {x + 5 - \frac{6}{{\sqrt {1 + 3x} {\rm{ \;}} + 2}} - \frac{2}{{\sqrt {2x - 1} {\rm{ \;}} + 1}}} \right) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1({\rm{tm}})}\\{x + 5 = \frac{6}{{\sqrt {1 + 3x} {\rm{ \;}} + 2}} + \frac{2}{{\sqrt {2x - 1} {\rm{ \;}} + 1}}}\end{array}} \right.}\end{array}\)
Xét phương trình \(x + 5 = \frac{6}{{\sqrt {1 + 3x} {\rm{ \;}} + 2}} + \frac{2}{{\sqrt {2x - 1} {\rm{ \;}} + 1}}\quad (*)\)
Do \(x \ge \frac{1}{2} \Rightarrow \frac{6}{{\sqrt {1 + 3x} {\rm{ \;}} + 2}} + \frac{2}{{\sqrt {2x - 1} {\rm{ \;}} + 1}} < \frac{6}{2} + \frac{2}{1} = 5\) và \(x + 5 \ge \frac{{11}}{2} > 5\)
nên phương trình \((*)\) vô nghiệm.
Vậy phương trình đã cho có nghiệm duy nhất \(x = 1\).
b) Từ giả thiết \(x + y + z = 1\) \( \Rightarrow x + yz = x\left( {x + y + z} \right) + yz = \left( {x + y} \right)\left( {x + z} \right)\)
Tương tự \(y + zx = \left( {y + z} \right)\left( {y + x} \right);z + xy = \left( {z + x} \right)\left( {z + y} \right)\)
Do đó \(P = \frac{{\left( {x + y} \right)\left( {x + z} \right)}}{{y + z}} + \frac{{\left( {y + z} \right)\left( {y + x} \right)}}{{z + x}} + \frac{{\left( {z + x} \right)\left( {z + y} \right)}}{{x + y}}\)
Đặt \(x + y = a,y + z = b,z + x = c \Rightarrow a,b,c > 0\) và \(a + b + c = 2\).
\(P = \frac{1}{2}\left[ {\left( {\frac{{ab}}{c} + \frac{{ac}}{b}} \right) + \left( {\frac{{bc}}{a} + \frac{{ba}}{c}} \right) + \left( {\frac{{ca}}{b} + \frac{{cb}}{a}} \right)} \right]\)
\( \ge \frac{1}{2}\left( {2\sqrt {\frac{{ab}}{c} \cdot \frac{{ac}}{b}} {\rm{ \;}} + 2\sqrt {\frac{{bc}}{a} \cdot \frac{{ba}}{c}} {\rm{ \;}} + 2\sqrt {\frac{{ca}}{b} \cdot \frac{{cb}}{a}} } \right) = a + b + c = 2\)
Dấu " =" xảy ra khi \(a = b = c = \frac{2}{3}\).
Vậy giá trị lớn nhất của biểu thức \(P\) bằng 2 khi \(x = y = z = \frac{1}{3}\).