Đề thi vào 10 môn Toán Nghệ An năm 2020
Tải vềCâu 1: a) Tính
Đề bài
Câu 1:
a) Tính \(A = \sqrt {{{\left( {1 - 2\sqrt 5 } \right)}^2}} - \sqrt {20} \)
b) Rút gọn biểu thức \(B = \left( {\dfrac{{\sqrt x }}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}}} \right).\dfrac{1}{{\sqrt x + 1}}\) với \(x \ge 0\) và \(x \ne 4\).
c) Tìm giá trị của tham số \(m\) để đường thẳng \(y = \left( {{m^2} + 1} \right)x + m\) song song với đường thẳng \(y = 5x + 2\).
Câu 2:
a) Giải phương trình \({x^2} - 5x + 6 = 0\)
b) Cho phương trình \({x^2} - 4x - 3 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị của biểu thức \(T = \dfrac{{x_1^2}}{{{x_2}}} + \dfrac{{x_2^2}}{{{x_1}}}\).
Câu 3:
Hưởng ứng phương trào toàn dân chung tay đẩy lùi đại dịch Covid-19, trong tháng hai năm 2020, hai lớp 9A và 9B của một trường THCS đã nghiên cứu và sản suất được 250 chai nước rửa tay sát khuẩn. Vì muốn tặng quà cho khu cách li tập trung trên địa bàn, trong tháng ba, lớp 9A làm vượt mức 25%, lớp 9B làm vượt mức 20%, do đó tổng sản phẩm của cả hai lớp vượt mức 22% so với tháng hai. Hỏi trong tháng hai, mỗi lớp đã sản xuất được bao nhiêu chai nước rửa tay sát khuẩn?
Câu 4:
Cho tứ giác ABCD (AD > BC) nội tiếp đường tròn tâm O đường kính AB. Hai đường chéo AC và BD cắt nhau tại E. Gọi H là hình chiếu của E trên AB.
a) Chứng minh ADEH là tứ giác nội tiếp.
b) Tia CH cắt đường tròn (O) tại điểm thứ hai là K. Gọi I là giao điểm của DK và AB. Chứng minh \(D{I^2} = AI.BI\).
c) Khi tam giác DAB không cân, gọi M là trung điểm của EB, tia DC cắt tia HM tại N. Tia NB cắt đường tròn ngoại tiếp tam giác HMB tại điểm thứ hai là F. Chứng minh F thuộc đường tròn (O).
Câu 5:
Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^3} + 2{y^2} + x{y^2} = 2 + x - 2{x^2}\\4{y^2} = \left( {\sqrt {{y^2} + 1} + 1} \right)\left( {{y^2} - {x^3} + 3x - 2} \right)\end{array} \right.\)
Lời giải chi tiết
Câu 1 (2,5 điểm)
Cách giải:
a) Tính \(A = \sqrt {{{\left( {1 - 2\sqrt 5 } \right)}^2}} - \sqrt {20} \)
Ta có:
\(\begin{array}{l}A = \sqrt {{{\left( {1 - 2\sqrt 5 } \right)}^2}} - \sqrt {20} \\\,\,\,\,\, = \left| {1 - 2\sqrt 5 } \right| - \sqrt {{2^2}.5} \\\,\,\,\,\, = 2\sqrt 5 - 1 - 2\sqrt 5 \\\,\,\,\,\, = - 1\end{array}\)
Vậy \(A = - 1\).
b) Rút gọn biểu thức \(B = \left( {\dfrac{{\sqrt x }}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}}} \right).\dfrac{1}{{\sqrt x + 1}}\) với \(x \ge 0\) và \(x \ne 4\) .
Ta có:
\(\begin{array}{l}B = \left( {\dfrac{{\sqrt x }}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}}} \right).\dfrac{1}{{\sqrt x + 1}}\\B = \left( {\dfrac{{\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{1}{{\sqrt {x - 2} }}} \right).\dfrac{1}{{\sqrt x + 1}}\\B = \dfrac{{\sqrt x + \sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}.\dfrac{1}{{\sqrt x + 1}}\\B = \dfrac{{2\sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}.\dfrac{1}{{\sqrt x + 1}}\\B = \dfrac{{2\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}.\dfrac{1}{{\sqrt x + 1}}\\B = \dfrac{2}{{x - 4}}\end{array}\)
Vậy \(B = \dfrac{2}{{x - 4}}\) với \(x \ge 0\) và \(x \ne 4\).
c) Tìm giá trị của tham số \(m\) để đường thẳng \(y = \left( {{m^2} + 1} \right)x + m\) song song với đường thẳng \(y = 5x + 2\) .
Để đường thẳng \(y = \left( {{m^2} + 1} \right)x + m\) song song với đường thẳng \(y = 5x + 2\) thì:
\(\left\{ \begin{array}{l}{m^2} + 1 = 5\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 4\\m \ne 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m = \pm 2\\m \ne 2\end{array} \right. \Leftrightarrow m = - 2\)
Vậy \(m = - 2\).
Câu 2 (2,0 điểm)
Cách giải:
a) Giải phương trình \({x^2} - 5x + 6 = 0\)
\(\Delta = {5^2} - 4.1.6 = 1 > 0\)
\( \Rightarrow \left\{ \begin{array}{l}{x_1} = \dfrac{{5 + \sqrt 1 }}{2} = 3\\{x_2} = \dfrac{{5 - \sqrt 1 }}{2} = 2\end{array} \right.\)
Vậy phương trình có hai nghiệm phân biệt \({x_1} = 3,{x_2} = 2\).
b) Cho phương trình \({x^2} - 4x - 3 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\) . Không giải phương trình, hãy tính giá trị của biểu thức \(T = \dfrac{{x_1^2}}{{{x_2}}} + \dfrac{{x_2^2}}{{{x_1}}}\) .
Ta thấy \(a.c = 1.\left( { - 3} \right) = - 3 < 0\) nên phương trình luôn có hai nghiệm phân biệt \({x_1},{x_2} \ne 0\) thỏa mãn \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}{x_2} = - 3\end{array} \right.\)
Khi đó,
\(\begin{array}{l}T = \dfrac{{x_1^2}}{{{x_2}}} + \dfrac{{x_2^2}}{{{x_1}}} = \dfrac{{x_1^3 + x_2^3}}{{{x_1}{x_2}}}\\\,\,\,\,\, = \dfrac{{{{\left( {{x_1} + {x_2}} \right)}^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}}\\\,\,\,\,\, = \dfrac{{{4^3} - 3.\left( { - 3} \right).4}}{{ - 3}}\\\,\,\,\,\, = - \dfrac{{100}}{3}\end{array}\)
Vậy \(T = - \dfrac{{100}}{3}\).
Câu 3 (1,5 điểm)
Cách giải:
Hưởng ứng phương trào toàn dân chung tay đẩy lùi đại dịch Covid-19, trong tháng hai năm 2020, hai lớp 9A và 9B của một trường THCS đã nghiên cứu và sản suất được 250 chai nước rửa tay sát khuẩn. Vì muốn tặng quà cho khu cách li tập trung trên địa bàn, trong tháng ba, lớp 9A làm vượt mức 25%, lớp 9B làm vượt mức 20%, do đó tổng sản phẩm của cả hai lớp vượt mức 22% so với tháng hai. Hỏi trong tháng hai, mỗi lớp đã sản xuất được bao nhiêu chai nước rửa tay sát khuẩn?
Gọi số chai nước rửa tay lớp 9A, 9B lần lượt sản xuất được trong tháng hai là \(x,y\) (chai, \(x,y \in {\mathbb{N}^*},x,y < 250\))
Trong tháng hai, hai lớp sản suất được 250 chai nước rửa tay nên \(x + y = 250\) (1)
Số chai nước rửa tay lớp 9A sản xuất được trong tháng ba là:
\(x + 25\% x = x + 0,25x = 1,25x\) chai
Số chai nước rửa tay lớp 9B sản xuất được trong tháng ba là:
\(y + 20\% y = y + 0,2y = 1,2y\) chai
Số chai nước rửa tay cả hai lớp sản xuất được trong tháng ba là:
\(250 + 250.22\% = 305\) chai
Trong tháng ba, hai lớp sản suất được 305 chai nước rửa tay nên \(1,25x + 1,2y = 305\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 250\\1,25x + 1,2y = 305\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1,2x + 1,2y = 300\\1,25x + 1,2y = 305\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}0,05x = 5\\x + y = 250\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 100\\y = 150\end{array} \right.\,\,\,\,\left( {TM} \right)\).
Vậy lớp 9A sản suất được \(100\) chai nước rửa tay.
lớp 9B sản suất được \(150\) chai nước rửa tay.
Câu 4 (3,0 điểm)
Cách giải:
Cho tứ giác ABCD (AD > BC) nội tiếp đường tròn tâm O đường kính AB. Hai đường chéo AC và BD cắt nhau tại E. Gọi H là hình chiếu của E trên AB.
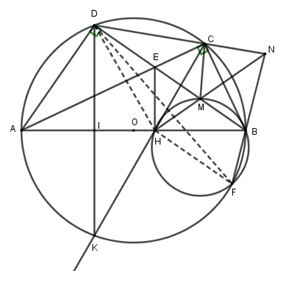
a) Chứng minh ADEH là tứ giác nội tiếp.
Ta có: \(\angle ADB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\(EH \bot AB \Rightarrow \angle AHE = {90^0}\)
Tứ giác ADEH có: \(\angle ADE + \angle AHE = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (đpcm)
b) Tia CH cắt đường tròn (O) tại điểm thứ hai là K. Gọi I là giao điểm của DK và AB. Chứng minh \(D{I^2} = AI.BI\) .
Tứ giác ADCK nội tiếp nên \(\angle ADK = \angle ACK\) (hai góc nội tiếp cùng chắn cung \(AK\)) (1)
Xét tứ giác ECBH có:
\(\angle ECB = \angle ACB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\(\angle EHB = {90^0}\left( {do\,\,EH \bot AB} \right)\)
\( \Rightarrow \angle ECB + \angle EHB = {90^0} + {90^0} = {180^0}\)
Do đó tứ giác ECBH nội tiếp (tứ giác có hai góc đối có tổng số đo bằng \({180^0}\))
\( \Rightarrow \angle ECH = \angle EBH\) (hai góc nội tiếp cùng chắn cung EH)
\( \Rightarrow \angle ACK = \angle DBA\) (2)
Từ (1) và (2) suy ra \(\angle ADK = \angle DBA \Rightarrow \angle ADI = \angle DBA\)
Lại có \(\angle DBA + \angle DAB = {90^0}\) nên \(\angle ADI + \angle DAB = {90^0}\) hay \(\angle ADI + \angle DAI = {90^0}\)
\( \Rightarrow \angle DIA = {180^0} - \left( {\angle ADI + \angle DAI} \right) = {180^0} - {90^0} = {90^0}\)
\( \Rightarrow DI \bot AB\) nên DI là đường cao trong tam giác vuông ADB
\( \Rightarrow D{I^2} = IA.IB\) (hệ thức giữa cạnh và đường cao trong tam giác vuông) (đpcm)
c) Khi tam giác DAB không cân, gọi M là trung điểm của EB, tia DC cắt tia HM tại N. Tia NB cắt đường tròn ngoại tiếp tam giác HMB tại điểm thứ hai là F. Chứng minh F thuộc đường tròn (O).
Theo câu b, \(DK \bot BA\) tại \(I\) nên AB là đường trung trực của DK
\( \Rightarrow DA = AK\) \( \Rightarrow sd\,cung\,AD = sd\,cung\,AK\)
\( \Rightarrow \angle DCA = \angle ACK\) \( \Rightarrow CA\) là tia phân giác của góc \(\angle DCH\)
\( \Rightarrow \angle DCH = 2\angle ECH\) (3)
Tam giác EHB vuông tại H có M là trung điểm EB nên \(HM\) là đường trung tuyến
\( \Rightarrow MH = MB \Rightarrow \Delta MHB\) cân tại \(M\)
\( \Rightarrow \angle DMH = \angle MHB + \angle MBH = 2\angle MBH = 2\angle EBH\) (4)
Tứ giác ECBH có: \(\angle ECB + \angle EHB = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\))
\( \Rightarrow \angle ECH = \angle EBH\) (5)
Từ (3), (4) và (5) suy ra \(\angle DCH = \angle DMH\)
\( \Rightarrow DCMH\) là tứ giác nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh đối diện các góc bằng nhau)
\( \Rightarrow \angle NCM = \angle NHD\) (tính chất)
Xét \(\Delta NCM\) và \(\Delta NHD\) có:
Góc \(N\) chung
\(\angle NCM = \angle NHD\,\,\left( {cmt} \right)\)
\( \Rightarrow \Delta NCM \sim \Delta NHD\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{NC}}{{NH}} = \dfrac{{NM}}{{ND}}\) (cạnh tương ứng)
\( \Rightarrow NC.ND = NM.NH\) (6)
Tứ giác \(HMBF\) nội tiếp nên \(\angle NMB = \angle NFH\) (tính chất)
Xét \(\Delta NMB\) và \(\Delta NFH\) có:
Góc \(N\) chung
\(\angle NMB = \angle NFH\) (cmt)
\( \Rightarrow \Delta NMB \sim \Delta NFH\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{NM}}{{NF}} = \dfrac{{NB}}{{NH}}\) (cạnh tương ứng)
\( \Rightarrow NM.NH = NB.NF\) (7)
Từ (6) và (7) suy ra \(NC.ND = NF.NB \Rightarrow \dfrac{{NC}}{{NF}} = \dfrac{{NB}}{{ND}}\)
Xét \(\Delta NBC\) và \(\Delta NDF\) có:
Góc \(N\) chung
\(\begin{array}{l}\dfrac{{NC}}{{NF}} = \dfrac{{NB}}{{ND}}\left( {cmt} \right)\\ \Rightarrow \Delta NBC \sim \Delta NDF\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow \angle NCB = \angle NFD = \angle BFD\) (góc tương ứng)
Mà \(\angle NCB + \angle DCB = {180^0}\) (kề bù)
Nên \(\angle BFD + \angle DCB = {180^0}\)
Do đó tứ giác DCBF nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\))
Vậy điểm F nằm trên đường tròn (O) (đpcm).
Câu 5 (1,0 điểm)
Cách giải:
Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^3} + 2{y^2} + x{y^2} = 2 + x - 2{x^2}\\4{y^2} = \left( {\sqrt {{y^2} + 1} + 1} \right)\left( {{y^2} - {x^3} + 3x - 2} \right)\end{array} \right.\)
Đặt \(\left\{ \begin{array}{l}{x^3} + 2{y^2} + x{y^2} = 2 + x - 2{x^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\4{y^2} = \left( {\sqrt {{y^2} + 1} + 1} \right)\left( {{y^2} - {x^3} + 3x - 2} \right)\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow \left( {{x^3} + 2{x^2} - x - 2} \right) + \left( {2{y^2} + x{y^2}} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {{x^2} - 1} \right) + {y^2}\left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {{x^2} - 1 + {y^2}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\{x^2} - 1 + {y^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2\\{y^2} = 1 - {x^2}\end{array} \right.\end{array}\)
TH1: \(x = - 2\) thay vào \(\left( 2 \right)\) được:
\(\begin{array}{l}4{y^2} = \left( {\sqrt {{y^2} + 1} + 1} \right)\left( {{y^2} + 8 - 6 - 2} \right) \Leftrightarrow 4{y^2} = \left( {\sqrt {{y^2} + 1} + 1} \right).{y^2}\\ \Leftrightarrow {y^2}\left( {\sqrt {{y^2} + 1} + 1 - 4} \right) = 0 \Leftrightarrow {y^2}\left( {\sqrt {{y^2} + 1} - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{y^2} = 0\\\sqrt {{y^2} + 1} - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = 0\\{y^2} + 1 = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = 0\\{y^2} = 8\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = 0\\y = \pm 2\sqrt 2 \end{array} \right.\end{array}\)
TH2: \({y^2} = 1 - {x^2}\) thay vào (2) được:
\(\begin{array}{l}4\left( {1 - {x^2}} \right) = \left( {\sqrt {2 - {x^2}} + 1} \right)\left( {1 - {x^2} - {x^3} + 3x - 2} \right)\\ \Leftrightarrow 4\left( {1 - {x^2}} \right) = \left( {\sqrt {2 - {x^2}} + 1} \right)\left( { - {x^3} - {x^2} + 3x - 1} \right)\\ \Leftrightarrow 4\left( {{x^2} - 1} \right) = \left( {\sqrt {2 - {x^2}} + 1} \right)\left( {{x^3} + {x^2} - 3x + 1} \right)\\ \Leftrightarrow 4\left( {{x^2} - 1} \right) = \left( {\sqrt {2 - {x^2}} + 1} \right)\left( {x - 1} \right)\left( {{x^2} + 2x - 1} \right)\\ \Leftrightarrow 4\left( {x - 1} \right)\left( {x + 1} \right) = \left( {\sqrt {2 - {x^2}} + 1} \right)\left( {x - 1} \right)\left( {{x^2} + 2x - 1} \right)\\ \Leftrightarrow \left( {x - 1} \right)\left[ {4x + 4 - \left( {\sqrt {2 - {x^2}} + 1} \right)\left( {{x^2} + 2x - 1} \right)} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\4x + 4 - \left( {\sqrt {2 - {x^2}} + 1} \right)\left( {{x^2} + 2x - 1} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\4x + 4 = \left( {\sqrt {2 - {x^2}} + 1} \right)\left( {{x^2} + 2x - 1} \right)\end{array} \right.\end{array}\)
Với \(x = 1\) thì \({y^2} = 1 - 1 = 0 \Leftrightarrow y = 0\).
Với \(4x + 4 = \left( {\sqrt {2 - {x^2}} + 1} \right)\left( {{x^2} + 2x - 1} \right)\) ta có:
\(\begin{array}{l}4x + 4 = \left( {\sqrt {2 - {x^2}} + 1} \right)\left( {{x^2} + 2x - 1} \right)\\ \Leftrightarrow 4x + 4 = \sqrt {2 - {x^2}} \left( {{x^2} + 2x - 1} \right) + {x^2} + 2x - 1\\ \Leftrightarrow \sqrt {2 - {x^2}} \left( {{x^2} + 2x - 1} \right) = - {x^2} + 2x + 5\\ \Leftrightarrow \sqrt {2 - {x^2}} = \dfrac{{ - {x^2} + 2x + 5}}{{{x^2} + 2x - 1}}\\ \Leftrightarrow \sqrt {2 - {x^2}} = \dfrac{{6 - {{\left( {x - 1} \right)}^2}}}{{{{\left( {x + 1} \right)}^2} - 2}}\,\,\,\,\,\left( * \right)\end{array}\)
(Do \({x^2} + 2x - 1 = 0 \Leftrightarrow x = - 1 \pm \sqrt 2 \) không thỏa mãn phương trình)
Vì \({x^2} + {y^2} = 1\) nên \({x^2} \le 1 \Rightarrow - 1 \le x \le 1\)
\( \Rightarrow 1 \le \sqrt {2 - {x^2}} \le \sqrt 2 \) hay \(1 \le VT\left( * \right) \le \sqrt 2 \)
Lại có,
Với \(x \le 1\) thì \(\dfrac{{6 - {{\left( {x - 1} \right)}^2}}}{{{{\left( {x + 1} \right)}^2} - 2}} \ge \dfrac{{6 - {{\left( {1 - 1} \right)}^2}}}{{{{\left( {1 + 1} \right)}^2} - 2}} = 3 \Rightarrow VP\left( * \right) \ge 3\)
Với \(x \ge - 1\) thì \(\dfrac{{6 - {{\left( {x - 1} \right)}^2}}}{{{{\left( {x + 1} \right)}^2} - 2}} \le \dfrac{{6 - {{\left( { - 1 - 1} \right)}^2}}}{{{{\left( { - 1 + 1} \right)}^2} - 2}} = - 1 \Rightarrow VP\left( * \right) \le - 1\)
Do đó với \( - 1 \le x \le 1\) thì \(VP\left( * \right) \ge 3\) hoặc \(VP\left( * \right) \le - 1\).
\( \Rightarrow \) (*) vô nghiệm do \(1 \le VT\left( * \right) \le \sqrt 2 \) và \(VP\left( * \right) \ge 3\) hoặc \(VP\left( * \right) \le - 1\).
Vậy hệ đã cho có nghiệm \(\left( {x;y} \right) \in \left\{ {\left( { - 2;0} \right),\left( { - 2; - 2\sqrt 2 } \right),\left( { - 2;2\sqrt 2 } \ri