Giải bài 10 trang 62 sách bài tập toán 8 – Cánh diều
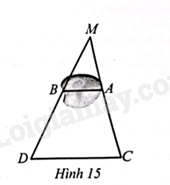
Trong công viên có một dẻo đất có dạng hình tam giác \(MCD\) được mô tả như Hình 15. Giữa hai điểm \(A,B\) là một hồ nước sâu và một con đường đi bộ giữa \(C\) và \(D\).
Đề bài
Trong công viên có một dẻo đất có dạng hình tam giác \(MCD\) được mô tả như Hình 15. Giữa hai điểm \(A,B\) là một hồ nước sâu và một con đường đi bộ giữa \(C\) và \(D\). Bạn An đi từ \(C\) đến \(D\) với tốc độ 100 m/phút trong thời gian 2 phút 42 giây. Tính độ dài \(AB\), biết \(AB//CD\) và \(MB = \frac{4}{5}BD\).
Phương pháp giải - Xem chi tiết
Áp dụng định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
Do \(MB = \frac{4}{5}BD\) nên \(MB = \frac{4}{9}MD\).
Do \(AB//CD\) nên theo hệ quả của định lí Thales, ta có:
\(\frac{{AB}}{{CD}} = \frac{{MB}}{{MD}} = \frac{4}{9}\) hay \(AB = \frac{4}{9}CD\).
Mặt khác, \(CD = 100.\frac{{27}}{{10}} = 270\) (m)
Vậy độ dài \(AB\) là: \(\frac{4}{9}.270 = 120\) (m).