Giải Bài 10 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.
Đề bài
Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.
Phương pháp giải - Xem chi tiết
Ta chứng minh N là trực tâm của tam giác MIK
Lời giải chi tiết
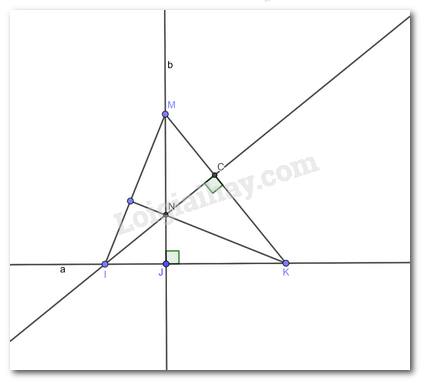
Vì b vuông góc với a tại J (theo giả thiết) và M thuộc b
\( \Rightarrow MJ \bot IK\)(1)
Vì đường thẳng qua I vuông góc với MK và cắt b tại N (gọi C là giao của MK và đường thẳng qua I vuông góc với MK)
\( \Rightarrow MK \bot IC\)(2)
Từ (1) và (2)\( \Rightarrow \)N là trực tâm ΔMIK
\( \Rightarrow \)NK là đường cao của ΔMIK (Các đường cao trong tam giác đi qua trực tâm)
\( \Rightarrow \)KN \( \bot \)MI