Giải Bài 8 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Ở Hình 1, cho biết AE = AF và $\widehat {ABC} = \widehat {ACB}$. Chứng minh AH là đường trung trực của BC.

Lời giải chi tiết

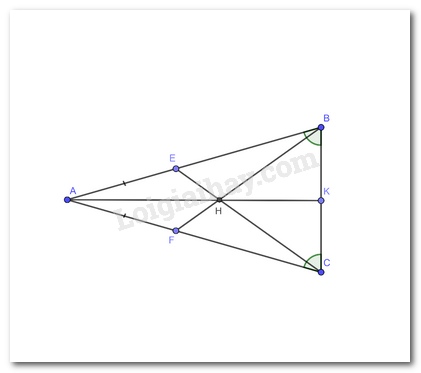
Theo giả thiết ta có tam giác ABC cân tại A do có 2 góc đáy bằng nhau

$\Rightarrow$A cách đều 2 đều B, C

$\Rightarrow$ A thuộc trung trực đoạn thẳng BC (1) (Tính chất điểm cách đều 2 đầu mút đoạn thẳng)

Xét $\Delta$AEC và $\Delta$AFB ta có :

AE = AF

Góc A chung

AC = AB

$\Rightarrow \Delta AEC = \Delta AFB$(c-g-c)

$\Rightarrow \widehat {ECA} = \widehat {FBA}$(góc tương ứng)

Ta có: $\widehat {ABC} = \widehat {ABF} + \widehat {FBC}$

$\widehat {ACB} = \widehat {ACE} + \widehat {ECB}$

Mà $\widehat {ACB} = \widehat {ABC}$(giả thiết) và $\widehat {ECA} = \widehat {FBA}$(chứng minh trên)

$\Rightarrow \widehat {ECB} = \widehat {FBC}$$\Rightarrow$$\Delta$HBC cân tại H do có 2 góc đáy bằng nhau

$\Rightarrow$ H cách đều BC $\Rightarrow$ H thuộc trung trực BC (2) (Tính chất điểm cách đều 2 đầu mút đoạn thẳng)

Từ (1) và (2) $\Rightarrow$ AH là trung trực của BC