Giải bài 11 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
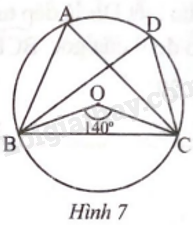
Cho bốn điểm A, B, C, D trên đường tròn (O) như Hình 7. a) (widehat {BOC}) là góc nội tiếp chắn cung (oversetfrown{BC}) của đường tròn (O). b) (widehat {OBC} = {40^o}) c) (widehat {BAC} = widehat {BDC}) d) (widehat {BAC} = 70{}^o)
Đề bài
Chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Cho bốn điểm A, B, C, D trên đường tròn (O) như Hình 7.
a) \(\widehat {BOC}\) là góc nội tiếp chắn cung \(\overset\frown{BC}\) của đường tròn (O).
b) \(\widehat {OBC} = {40^o}\)
c) \(\widehat {BAC} = \widehat {BDC}\)
d) \(\widehat {BAC} = 70{}^o\)
Phương pháp giải - Xem chi tiết
Dựa vào: Hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
a) Sai vì \(\widehat {BOC}\) là góc ở tâm chắn cung \(\overset\frown{BC}\) của đường tròn (O).
b) Sai vì \(\widehat {OBC} = \widehat {OCB} = \frac{{{{140}^o}}}{2} = {70^o}\) (do tam giác OBC cân tại O).
c) Đúng vì hai góc nội tiếp cùng chắn cung \(\overset\frown{BC}\).
d) Đúng vì \(\widehat {OBC} = \widehat {OCB} = \frac{{{{140}^o}}}{2} = {70^o}\) (do tam giác OBC cân tại O).