Giải bài 11 trang 136 SGK Toán 8 tập 2 - Kết nối tri thức
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC
Đề bài
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I. Chứng minh rằng
a) ΔBIC \(\backsim\) ΔEIF
b) \(F{B^2} = FI.FC\)
c) Cho biết AB = 6cm, BC = 3 cm. Tính EF
Phương pháp giải - Xem chi tiết
a) Chứng minh hai tam giác BIC và tam giác EIF có \(\widehat {IBC} = \widehat {IEF}{;^{}}\widehat {ICB} = \widehat {{\rm{IFE}}}\) (hai góc so le trong)
=> ΔBIC \(\backsim\) ΔEIF (g.g)
b) Sử dụng các tỉ số đồng dạng của hai tam giác để chứng minh \(F{B^2} = FI.FC\)
c) Tìm EF dựa vào định lý Thales.
Lời giải chi tiết
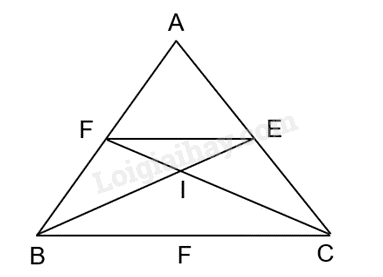
a) Vì tam giác ABC là tam giác cân
=> Hai đường phân giác đồng thời là đường trung tuyến
=> EF là đường trung bình của tam giác ABC
=> EF // BC
=> \(\widehat {IBC} = \widehat {IEF}{;^{}}\widehat {ICB} = \widehat {{\rm{IFE}}}\) (hai góc so le trong)
=> ΔBIC \(\backsim\) ΔEIF (g.g)
b) Vì tam giác ABC cân tại A
=> \(\widehat {ABE} = \widehat {EBC} = \widehat {ACF} = \widehat {FCB}\)
Xét tam giác FBI và tam giác FCB có góc F chung, $\widehat{FBI}=\widehat{FCB}$
=> ΔFBI \(\backsim\) ΔFCB (g.g)
=> \(\frac{{FB}}{{FC}} = \frac{{FI}}{{FB}}\)
=> \(F{B^2} = FI.FC\)
c) Ta có EF // BC (chứng minh trên). Do đó:
\( \frac{BC}{EF} = \frac{AB}{AF} \Rightarrow \frac{ (AF + FB)}{AF} = 1 + \frac{BC}{AB}=1+ \frac{3}{6} = \frac{3}{2} \)
Từ đó suy ra \( EF = 3 : \frac{3}{2} = 2 \) (cm)