Giải bài 12 trang 64 sách bài tập toán 8 - Chân trời sáng tạo tập 2
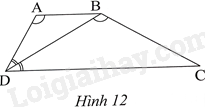
Trong Hình 12, cho biết tứ giác ABCD là hình thang. Biết DB là tia phân giác của góc ADC và \(\widehat {DAB} = \widehat {DBC}\).
Đề bài
Trong Hình 12, cho biết tứ giác ABCD là hình thang. Biết DB là tia phân giác của góc ADC và \(\widehat {DAB} = \widehat {DBC}\). Chứng minh rằng:
a) $\Delta ABD\backsim \Delta BDC$.
b) \(B{D^2} = AB.DC\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để chứng minh: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
a) Vì ABCD là hình thang nên AB//CD, do đó, \(\widehat {ABD} = \widehat {BDC}\) (hai góc so le trong)
Tam giác ABD và tam giác BDC có: \(\widehat {ABD} = \widehat {BDC}\) (cmt), \(\widehat {DAB} = \widehat {DBC}\) nên $\Delta ABD\backsim \Delta BDC\left( g.g \right)$
b) Vì $\Delta ABD\backsim \Delta BDC\left( cmt \right)$ nên \(\frac{{AB}}{{BD}} = \frac{{BD}}{{DC}}\), do đó \(B{D^2} = AB.DC\).