Giải bài 17 trang 106 sách bài tập toán 9 - Cánh diều tập 1
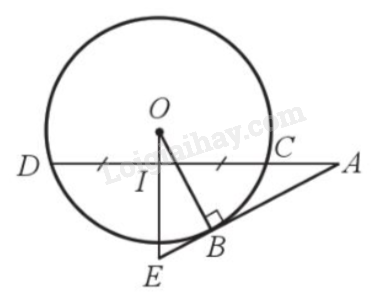
Từ điểm A ở ngoài đường tròn (O) vẽ tiếp tuyến AB của đường tròn với B là tiếp điểm. Lấy các điểm C, D thuộc đường tròn (O) sao cho C nằm giữa A và D, O không thuộc AD. Gọi I là trung điểm của đoạn thẳng CD, tia OI cắt AB tại E (Hình 16). Chứng minh: a) \(EB.EA = EI.EO\) b) \(A{B^2} = AC.AD\)
Đề bài
Từ điểm A ở ngoài đường tròn (O) vẽ tiếp tuyến AB của đường tròn với B là tiếp điểm. Lấy các điểm C, D thuộc đường tròn (O) sao cho C nằm giữa A và D, O không thuộc AD. Gọi I là trung điểm của đoạn thẳng CD, tia OI cắt AB tại E (Hình 16). Chứng minh:
a) \(EB.EA = EI.EO\)
b) \(A{B^2} = AC.AD\)
Phương pháp giải - Xem chi tiết
a) Bước 1: Chứng minh \(OI \bot CD\).
Bước 2: Chứng minh \(\Rightarrow \Delta AED \backsim \Delta ACB\left( {c.g.c} \right) \Rightarrow \angle ADE = \angle ABC\).
b) Bước 1: Chứng minh \(A{B^2} = O{A^2} - O{B^2} = O{A^2} - {R^2}\)
Bước 2: Chứng minh \(AC.AD = O{A^2} - {R^2}\)
Lời giải chi tiết
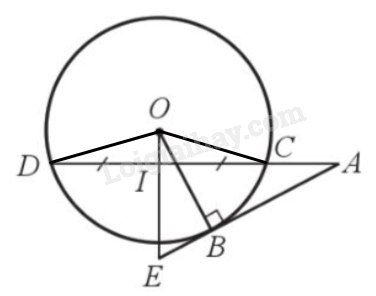
a) Kẻ OC, OD; suy ra \(OC = OD = R\)nên tam giác OCD cân tại O.
Có AB là tiếp tuyến của (O) nên \(\widehat {OBE} = \widehat {OBA} = 90^\circ \).
Xét tam giác OCD cân tại O có OI là đường trung tuyến (do I là trung điểm của CD) nên OI đồng thời là đường cao, do đó \(OI \bot CD\) hay \(\widehat {OIC} = \widehat {OID} = \widehat {AIE} = 90^\circ .\)
Xét 2 tam giác EOB và EAI có:
\(\widehat {OBE} = \widehat {AIE}\left( { = 90^\circ } \right)\)
\(\widehat E\) chung
Suy ra \(\Delta EOB\backsim \Delta EAI(g.g)\), do đó \(\frac{{EB}}{{EI}} = \frac{{EO}}{{EA}}\) hay \(EB.EA = EI.EO.\)
b) Áp dụng định lý Pythagore trong tam giác vuông OAB ta có:
\(A{B^2} = O{A^2} - O{B^2} = O{A^2} - {R^2}\)
Mặt khác, \(AC.AD = \left( {AI - CI} \right)\left( {AI + DI} \right)\), mà \(DI = CI\), suy ra
\(\begin{array}{l}AC.AD = \left( {AI - CI} \right)\left( {AI + CI} \right)\\ = A{I^2} - C{I^2}\\ = A{I^2} - \left( {O{C^2} - O{I^2}} \right)\\ = A{I^2} - O{C^2} + O{I^2}\\ = A{I^2} - {R^2} + O{A^2} - A{I^2}\\ = O{A^2} - {R^2}\end{array}\)
Do đó \(A{B^2} = AC.AD\left( { = O{A^2} - {R^2}} \right)\)