Giải bài 17 trang 90 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC cân ở A, H là trung điểm của BC và (widehat {BAC} < {90^o}). Đường vuông góc với AB tại A cắt đường thẳng BC ở D. Kẻ DE vuông góc với AC. Chứng minh: a) AH = EH b) (widehat {DCE} = widehat {ABD}).
Đề bài
Cho tam giác ABC cân ở A, H là trung điểm của BC và \(\widehat {BAC} < {90^o}\) . Đường vuông góc với AB tại A cắt đường thẳng BC ở D. Kẻ DE vuông góc với AC. Chứng minh:
a) AH = EH
b) \(\widehat {DCE} = \widehat {ABD}\) .
Phương pháp giải - Xem chi tiết
Chứng minh tam giác HAE cân tại H suy ra AH = EH.
Sử dụng tính chất bắc cầu: \(\widehat {DCE} = \widehat {ACH}\) mà \(\widehat {ACH} = \widehat {ABH}\) nên \(\widehat {DCE} = \widehat {ABD}\)
Lời giải chi tiết
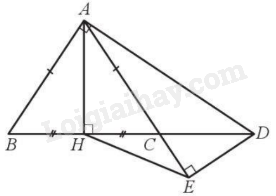
a) Do tam giác ABC cân tại A và H là trung điểm của BC nên \(\widehat {BAH} = \widehat {HAC}\) (1). Vì các tam giác AHD và AED lần lượt vuông tại H và E nên tứ giác AHED nội tiếp đường tròn đường kính AD suy ra \(\widehat {ADH} = \widehat {AEH}\) (2). Mặt khác \(\widehat {ADH} = \widehat {BAH}\) (3) (vì cùng cộng với \(\widehat {HAC}\) bằng 90 o ).
Từ (1), (2), (3) suy ra \(\widehat {HAC} = \widehat {AEH}\). Do đó, tam giác HAE cân tại H. Vì vậy AH = EH.
b) Ta có \(\widehat {DCE} = \widehat {ACH}\) (đối đỉnh) mà \(\widehat {ACH} = \widehat {ABH}\) (do tam giác ABC cân tại A) nên \(\widehat {DCE} = \widehat {ABH}\) hay \(\widehat {DCE} = \widehat {ABD}\).