Giải bài 2.12 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức
a) Giả sử G là một đồ thị với n đỉnh và (frac{{left( {n - 1} right)left( {n - 2} right)}}{2} + 2) cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton.
Đề bài
a) Giả sử G là một đồ thị với n đỉnh và \(\frac{{\left( {n - 1} \right)\left( {n - 2} \right)}}{2} + 2\) cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton.
b) Tìm một đồ thị với n đỉnh và \(\frac{{\left( {n - 1} \right)\left( {n - 2} \right)}}{2} + 1\) cạnh mà không có chu trình Hamilton.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức vừa học để làm
Lời giải chi tiết
a) Định lí Ore: Nếu G là một đồ thị có n đỉnh \(\left( {n \ge 3} \right)\) và mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n thì G có một chu trình Hamilton.
Ta có lí thuyết: Giả sử G là đồ thị đơn gồm n đỉnh và m cạnh. Nếu \(m \ge \;\frac{{{n^2} - 3n\; + 6}}{2}\) thì G là đồ thị có chu trình Hamilton.
Áp dụng vào bài toán ta được điều phải chứng minh.
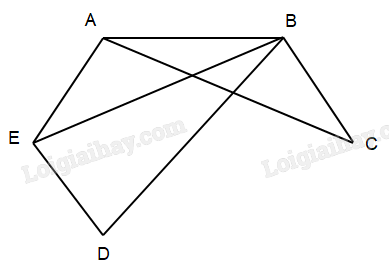
b) Ta có đồ thị sau có 5 đỉnh, 7 cạnh và đồ thị không có chu trình Hamilton.